Consumption-portfolio optimization with recursive utility in incomplete markets

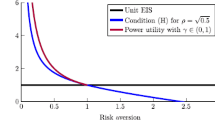
Abstract

In an incomplete market, we study the optimal consumption-portfolio decision of an investor with recursive preferences of Epstein–Zin type. Applying a classical dynamic programming approach, we formulate the associated Hamilton–Jacobi–Bellman equation and provide a suitable verification theorem. The proof of this verification theorem is complicated by the fact that the Epstein–Zin aggregator is non-Lipschitz, so standard verification results (e.g. in Duffie and Epstein, Econometrica 60, 393–394, 1992) are not applicable. We provide new explicit solutions to the Bellman equation with Epstein–Zin preferences in an incomplete market for non-unit elasticity of intertemporal substitution (EIS) and apply our verification result to prove that they solve the consumption-investment problem. We also compare our exact solutions to the Campbell–Shiller approximation and assess its accuracy.

Appendices

Appendix A: Generalization of Skiadas’ lemma

In this part of the appendix, we establish the key auxiliary result required in the proof of Theorem 3.1. Throughout Appendix A, we assume as given a probability space $(\varOmega,\mathfrak {F},\mathbb {P})$ endowed with an arbitrary filtration $\{\mathfrak {F}_{t}\}_{t\in[0,T]}$ satisfying the usual conditions of right-continuity and completeness; however, $\mathfrak {F}_{0}$ does not have to be trivial. First, recall

Theorem A.1

(Stochastic Gronwall–Bellman inequality)

Let Y={Y _t } _t∈[0,T] be a right-continuous adapted process with $\mathbb {E}[\sup_{s\in [0,T]}|Y_{s}|]<\infty$ and suppose that for some k∈(0,∞),

$$Y_t\ge k \mathbb {E}_t \biggl[{\int _t^T} Y_s\,\mathrm {d}{s} \biggr]\quad \text{\textit{a.s.\ for every}}\ t\in[0,T]. $$

Then Y _t ≥0 for all t∈[0,T] a.s.

For the proof of this result, we refer the reader to Appendix B in [11] or Appendix B in [20].

The main result of this appendix is the following generalization of Skiadas’ lemma.¹⁴ We wish to stress that Condition (A.1) of Theorem A.2 is only required on the event {Y _t ≤0}.

Theorem A.2

(Generalized Skiadas’ lemma)

Let Y={Y _t } _t∈[0,T] be a right-continuous adapted process with Y _T =0 and $\mathbb {E}[\sup_{s\in[0,T]}|Y_{s}|]<\infty$. Moreover, assume that there exist a progressive process H and a constant k∈(0,∞) such that

$$ Y_t = \mathbb {E}_t \biggl[{ \int _t^T} H_s\,\mathrm {d}{s} \biggr]\quad \text{\textit{a.s.\ and}}\ H_t\ge kY_t\ \text{\textit{on}}\ \{Y_t\le0\}\ \text{\textit{a.s.\ for}}\ t\in[0,T]. $$

(A.1)

Then Y _t ≥0 for all t∈[0,T] a.s.

Proof

Since Y is right-continuous, it suffices to prove $Y_{t_{0}}\ge0$ a.s. for each t ₀∈[0,T]. If the result is established for t ₀=0, then applying it to each of the processes $\{ Y_{t_{0}+t}\}_{t\in[0,T-t_{0}]}$ for t ₀∈[0,T] yields the claim.¹⁵ Thus it suffices to show that Y ₀≥0 a.s. We define the stopping time

$$\tau:=\inf\bigl\{{t\in[0,\infty)}\,:\,{Y_t>0}\bigr\}\wedge T. $$

Note that Y _τ ≥0 since Y is right-continuous and Y _T =0. By (A.1) it follows that $\{Y_{t}+\int_{0}^{t} H_{s}\,\mathrm {d}{s}\}_{t\in[0,T]}$ is a martingale. Hence the optional stopping theorem gives $\mathbb {E}_{t}[1_{\{\tau>t\}} ( Y_{\tau} + \int_{0}^{\tau } H_{s}\,\mathrm {d}{s})] = 1_{\{\tau>t\}} (Y_{t}+\int_{0}^{t} H_{s}\,\mathrm {d}{s})$ a.s., and so

$$ 1_{\{\tau>t\}}Y_t = \mathbb {E}_t \biggl[{ \int_t^{\tau}} 1_{\{\tau>t\}} H_s\,\mathrm {d}{s} + 1_{\{\tau>t\}}Y_{\tau} \biggr]\quad\text{a.s.\ for }t\in[0,T]. $$

(A.2)

The assumption on H yields H _t (ω)≥kY _t (ω) for all (t,ω)∈[0,T]×Ω with 0≤t<τ(ω), i.e., with Y _t (ω)≤0, and substituting this into (A.2), we get

$$1_{\{\tau>t\}}Y_t \ge \mathbb {E}_t \biggl[{ \int _t^{\tau}} 1_{\{\tau>t\}}H_s\,\mathrm {d}{s} \biggr] \ge k \mathbb {E}_t \biggl[{ \int_t^T} 1_{\{\tau>s\}}Y_s\,\mathrm {d}{s} \biggr]\quad\text{a.s.} $$

Applying the stochastic Gronwall–Bellman inequality in Theorem A.1 to the process {1_{τ>t} Y _t } _t∈[0,T], we find that 1_{τ>0} Y ₀≥0 a.s. By definition of τ, we have 1_{τ=0} Y ₀≥0. Hence, Y ₀≥0 a.s. □

Appendix B: General verification result

In Appendix B, we prove the general verification results of Sect. 3.

Proof of Theorem 3.1

We adapt the line of argument in the proof of Proposition 9 in [11]. Let x∈Ξ and $u=(\pi,c)\in \mathcal {A}(x)$ be an arbitrary admissible control. To shorten notation, X=X ^x,u and V=V ^c denote the controlled process and the continuation value process associated to u and c, respectively. Itô’s formula implies that

where M is a martingale. Taking conditional expectations and using the definition of V, we obtain

Hence,

$$ w(t,X_t)-V_t = - \mathbb {E}_t \biggl[\int_t^T \bigl \{L^{u_s}[w](s,X_s)+f(c_s,V_s)\bigr \} \,\mathrm {d}{s} \biggr]\quad\text{for }t\in[0,T]. $$

(B.3)

The dynamic programming equation implies

(B.4)

and condition (L) yields

$$ L^{u_s}[w](s,X_s)+f(c_s,V_s) \le k\bigl( V_s-w(s,X_s) \bigr)\quad\text{on}\ \bigl\{ V_s\ge w(s,X_s)\bigr\}. $$

(B.5)

Combining (B.1) with (B.3) we find that Y={Y _t } _t∈[0,T]:={w(t,X _t )−V _t } _t∈[0,T] has the representation

$$Y_t = \mathbb {E}_t \biggl[\int_t^T H_s\,\mathrm {d}{s} \biggr]\quad\text{with }H_t\ge kY_t\ \text{on }\{Y_t\le0\}. $$

Thus we can apply the generalized Skiadas’ lemma in Theorem A.2 and obtain $\mathfrak {v}(c) = V^{c}_{0} \le w(0,X^{x,u}_{0}) = w(0,x)$. Since $u=(\pi,c)\in \mathcal {A}(x)$ is arbitrary, we have

$$\sup _{u=(\pi,c)\in \mathcal {A}(x)} \mathfrak {v}(c) \le w(0,x). $$

Conversely, under the assumptions of Theorem 3.1, we have for the feedback control χ ^⋆ that

$$L^{u^{\star}(s,X_s)}[w](s,X_s)+f\bigl(c^{\star}_s,V_s \bigr) = f\bigl(c^{\star}_s,V_s\bigr)-f \bigl(c^{\star}_s,w(s,X_s) \bigr) $$

instead of (B.2), where $u^{\star}=\{ u^{\star}_{t}\}_{t\in[0,T]}:= \{\chi ^{\star}(t,X^{x,\chi ^{\star}}_{t})\}_{t\in[0,T]}$. Therefore, the preceding argument applies to both processes $\{w(t,X^{x,u^{\star}}_{t})-V^{c^{\star}}_{t}\}_{t\in[0,T]}$ and $\{ V^{c^{\star}}_{t}-w(t,X^{x,u^{\star}}_{t})\}_{t\in[0,T]}$. Consequently, $\mathfrak {v}(c^{\star}) = w(0,x)$ and $c^{\star }\in \mathcal {C}$. Hence χ ^⋆ is an optimal feedback control. □

We now provide a verification result for the associated infinite-horizon problem.

Corollary B.3

In the framework of Sect. 3, suppose that all coefficients are time-homogeneous and consider the infinite-horizon stochastic control problem to

Suppose that f satisfies condition (L), that w∈C²(Ξ) is a solution of

$$\sup _{u=(\pi,c)\in \varLambda (x)} L^u[w](x) + f \bigl(c,w(x) \bigr) = 0,\quad x\in\varXi, $$

and that for every $u\in \mathcal {A}(x)$ the local martingale

$$\int_0^{\:\cdot \:} \frac{\partial w}{\partial x} \bigl(X^{x,u}_s\bigr)^{\mathfrak {t}}a\bigl(X^{x,u}_s,u_s \bigr)\,\mathrm {d}{W}_s $$

is a uniformly integrable martingale. Further assume the transversality condition

$$\mathbb {E}\bigl[V^c_T\bigr]\to0\ \text{\textit{and}}\ \mathbb {E}\bigl[w\bigl(X^{x,u}_T\bigr)\bigr]\to0\quad\text{\textit{as}}\ T\to \infty \ \text{\textit{for all}}\ u=(\pi,c)\in \mathcal {A}(x). $$

If there is a feedback control $\chi ^{\star}=(\chi ^{\star }_{\pi},\chi ^{\star}_{c}):\ \varXi\to \mathbf {R}^{m}\times \mathsf {C}$ with

$$L^{\chi ^{\star}(x)}[w](x) + f \bigl(\chi ^{\star}_c(x), w(x) \bigr) = 0\quad\text{\textit{for all}}\ x\in\varXi, $$

then χ ^⋆ is optimal and w is the value function of problem (3.2). In particular,

$$w(x) = \max _{u=(\pi,c)\in \mathcal {A}(x)} \mathfrak {v}(c)\quad\text{\textit{for all}}\ x \in\varXi. $$

Proof

Let x∈Ξ and $u=(\pi,c)\in \mathcal {A}(x)$. We use similar notation as in the proof of Theorem 3.1; in particular, let X=X ^x,u and V=V ^c. For fixed T>0, define

$$\bar{V}^{(T)}_t := \mathbb {E}_t \biggl[ w(X_T) + \int_t^T f(c_s,V_s) \,\mathrm {d}{s} \biggr]\quad\text{for }t\in[0,T]. $$

Then it follows as in the proof of Theorem 3.1 that $w(x)\ge\bar{V}^{(T)}_{0}$. Since

$$V_t = \mathbb {E}_t \biggl[ V_T + \int _t^T f(c_s,V_s) \,\mathrm {d}{s} \biggr],\quad t\in[0,T], $$

the transversality condition implies that $V_{0} - \bar{V}^{(T)}_{0} = \mathbb {E}[V_{T}] - \mathbb {E}[w(X_{T})] \to0$ as T→∞. Thus we have $w(x)\ge V_{0} = \mathfrak {v}(c)$ and

$$\sup _{u=(\pi,c)\in \mathcal {A}(x)} \mathfrak {v}(c) \le w(x). $$

The remainder of the proof is analogous to that of Theorem 3.1. □

Proof of Proposition 3.2

Let c∈C be arbitrary, and let v,w∈V with v≥w. From the definition of the Epstein–Zin aggregator in (2.2), we have

(B.6)

Since the first summand is obviously Lipschitz, it is sufficient to show that in each of the cases (a)–(d), the second summand is negative. Note that

$$\frac{\delta}{1-\frac{1}{\psi}} c^{1-\frac{1}{\psi}}>0\quad\text {if and only if}\quad \psi>1. $$

If γ<1, i.e., 1−γ>0, then (1−γ)v≥(1−γ)w and

$$1-\frac{1-\frac{1}{\psi}}{1-\gamma}>0\quad\text{if and only if}\quad \gamma<\frac{1}{\psi}. $$

Thus, in this case the second summand in (B.4) is negative if

$$\psi>1\ \text{and }\gamma\ge\frac{1}{\psi},\quad\text{or}\quad \psi <1\ \text{and}\ \gamma<\frac{1}{\psi}. $$

However, if ψ<1 then $\gamma<1<\frac{1}{\psi}$ is always satisfied, and we obtain cases (c) and (d). Similarly, if γ>1, i.e., 1−γ<0, then (1−γ)v≤(1−γ)w and

$$1-\frac{1-\frac{1}{\psi}}{1-\gamma}>0\quad\text{if and only if}\quad \gamma>\frac{1}{\psi}. $$

Hence, the second summand in (B.4) is negative if

$$\psi>1\ \text{and }\gamma>\frac{1}{\psi},\quad\text{or}\quad \psi<1\ \text{and } \gamma\le\frac{1}{\psi}. $$

Now we always have $\gamma>1>\frac{1}{\psi}$ for ψ>1, and we obtain cases (a) and (b). □

Appendix C: Verification for Heston’s model

Appendix C provides the proof of Theorem 5.1. We first establish Theorem 5.1 assuming that Propositions C.3 and C.6 hold true. Then we present the proofs of Propositions C.3 and C.6.

Proof of Theorem 5.1

The proof is divided into two steps.

Step 1: Explicit solution of (4.5). First observe that

$$\tilde{r}(y) = -\frac{1}{k} \biggl[r(1-\gamma)-\delta\theta+ \frac{1}{2}\frac{1-\gamma}{\gamma}\bar{\lambda}^2 y \biggr ],\qquad \tilde{\alpha}(y) = \vartheta- \biggl(\kappa -\frac{1-\gamma }{\gamma}\bar{\lambda}\bar{ \beta}\rho\biggr)y. $$

It is then sufficient to solve the PDE (4.6) for h for every s∈[0,T]. The conjecture h(t,y;s)=e^{A(t,s)−B(t,s)y} yields for $A(\:\cdot \:,s)$ and $B(\:\cdot \:,s)$ the ODEs

The solutions read

(C.7)

where $\hat{\kappa } := \kappa -\frac{1-\gamma}{\gamma}\bar{\lambda }\bar{\beta}\rho$, $b:= -\frac{1}{2}\frac{1-\gamma}{k\gamma}\bar {\lambda}^{2}$ and $a :=\sqrt{\hat{\kappa }^{2}+2b\bar{\beta}^{2}}$.

Step 2: Verification of the integrability condition (M). Proposition C.3 implies that under the assumptions of Theorem 5.1 the integrability condition (M) holds for all $(\pi,c)\in \mathcal {A}'(x)$. Moreover, by Proposition C.6, the consumption-portfolio strategy (π ^⋆,c ^⋆) in (5.2) is admissible. Hence Theorem 3.1 yields the claim. □

In the remainder of this appendix, we complete the proof of Theorem 5.1 by establishing Propositions C.3 and C.6. In the following we suppose that the assumptions of Theorem 5.1 are satisfied. In particular, conditions (H) and (H1)–(H3) are assumed to hold. We also continue to use the notation introduced in Sect. 5.1 and the proof of Theorem 5.1. In particular,

Moreover, we define the processes $\pi^{\star}=\{\pi^{\star}_{t}\}$ and $C^{\star}=\{C^{\star}_{t}\}$ by

$$\pi^{\star}_t = \frac{1}{\gamma}\bar{\lambda}+ \frac{k}{\gamma}\bar{\beta}\rho\frac{g_y(t,Y_t)}{g(t,Y_t)} \quad \text{and}\quad C^{\star}_t := \frac{\delta^{\psi}}{g(t,Y_t)}, $$

which are the candidates for the optimal trading strategy and the optimal consumption–wealth ratio, respectively. Slightly abusing notation, we also write $\pi^{\star}_{t} = \pi^{\star}(t,Y_{t})$ and $C^{\star}_{t} = C^{\star}(t,Y_{t})$ for the feedback form of these strategies. Our first result summarizes some estimates of the functions g, A, and B.

Lemma C.4

We have

$$ \left |{\frac{g_y(t,y)}{g(t,y)}}\right | \le \left \|{B}\right \|\quad\text{\textit{and}}\quad 0 \le g(t,y) \le\mathrm{e}^{\left \|{A}\right \|}(T-t),\quad t\in[0,T],\ y\in [0,\infty), $$

(C.8)

where $\left \|{F}\right \| :=\max_{s,t\in[0,T],\, t\le s} |F(t,s)| < \infty$ for F∈{A,B}. More precisely, A and B satisfy

(C.9)

(C.10)

and we have

$$ \frac{\bar{\lambda}}{\gamma} \le\pi ^{\star}(t,y) \le K_\pi\quad\text{\textit{for all}}\ t\in[0,T],\ y\in[0,\infty). $$

(C.11)

Proof

First note that B(t,s)≥0 for t≤s. The first inequality in (C.2) follows from

$$\left |{\frac{g_y(t,y)}{g(t,y)}}\right | = \frac{\int_t^T \mathrm {e}^{A(t,s)-B(t,s)y}B(t,s)\,\mathrm {d}{s}}{\int_t^T \mathrm {e}^{A(t,s)-B(t,s)y}\,\mathrm {d}{s}} \le \left \|{B}\right \|, $$

and the second is immediate. To establish (C.3), recall that $B(\:\cdot \:,s)$ is given by

$$B_t(t,s) = \hat{\kappa } B(t,s) + \frac{1}{2}\bar{ \beta}^2B(t,s)^2 - b,\qquad B(s,s)=0. $$

Since $\hat{\kappa }>0$ by assumption and b>0, an elementary ODE argument yields the first part of (C.3). The second estimate follows from (C.1). To prove (C.4), recall that $A(\:\cdot \:,s)$ is given by

$$A(t,s) = -\vartheta{ \int_t^s} B(\tau,s) \,\mathrm {d}\tau+ \frac{(1-\gamma)r-\delta\theta}{k}(s-t)\quad\text{for}\ t\le s. $$

Observe that $\frac{(1-\gamma)r-\delta\theta}{k}<0$ since γ>1 and θ,k>0. Therefore, by (C.3), we obtain

$$A(t,s) \ge-\vartheta{ \int_t^s} B(\tau,s) \,\mathrm {d}\tau\ge-\vartheta{\int_t^s} b(\tau-s) \,\mathrm {d}\tau= -\frac{1}{2}\vartheta b(s-t)^2. $$

Hence (C.4) follows. Finally, (C.5) follows from the definition of π ^⋆ since ρ≤0 and $\frac{g_{y}(t,y)}{g(t,y)}\le0$ as well as (C.2), (C.3). □

Next we recall a well-known result on the Laplace transform of the integrated square-root process; see [25].

Lemma C.5

(Pitman–Yor)

Consider the square-root process Y={Y _t } with dynamics

$$\mathrm {d}{Y}_t=(\vartheta-\kappa Y_t)\,\mathrm {d}{t} + \bar{\beta} \sqrt{Y_t}\,\mathrm {d}\bar{W}_t, $$

where $\bar{W}=\{\bar{W}_{t}\}$ is a standard Wiener process. Further assume that p,q∈R satisfy

$$q \le\frac{\kappa ^2}{2\bar{\beta}^2}\quad\text{\textit{and}}\quad p \le \frac{\kappa +\sqrt{\kappa ^2+2\bar{\beta}^2 q}}{\bar{\beta}^2}. $$

Then the Laplace transform

$$\varphi(t,T,y) := \mathbb {E}\biggl[ \exp\biggl\{ p Y_T + q{ \int _t^T} Y_s\,\mathrm {d}{s} \biggr\} \biggl|\ Y_t=y \biggr] $$

is well-defined and

$$\varphi(t,T,y) = \mathrm{e}^{\tilde{A}(t,T)+\tilde{B}(t,T)y}, $$

where $\tilde{A}(\:\cdot \:,T)$ and $\tilde{B}(\:\cdot \:,T)$ are bounded continuous functions on [0,T].

Proposition C.6

(Verification of integrability condition (M))

Under the assumptions of Theorem 5.1, the integrability condition (M) holds for all $(\pi,c)\in \mathcal {A}'(x)$.

Proof

Let $(\pi,c)\in \mathcal {A}'(x)$ be an admissible consumption-portfolio strategy. To establish (M), we have to show that

$$\mathbb {E}\biggl[{ \int_0^T} \bigl(F_t^2 + \hat{F}_t^2\bigr) \,\mathrm {d}{t} \biggr] < \infty, $$

where the processes F={F _t } and $\hat{F}=\{\hat{F}_{t}\}$ are given by

As π and $\{\frac{g_{y}(t,Y_{t})}{g(t,Y_{t})}\}$ are uniformly bounded and

it suffices to show that

$$\mathbb {E}\biggl[{ \int_0^T} G_t^2 \,\mathrm {d}{t} \biggr] = \int_0^T \mathbb {E}\bigl[G_t^2\bigr] \,\mathrm {d}{t} < \infty,\quad \text{where}\ G_t:= X_t^{1-\gamma}g(t,Y_t)^k (1+\sqrt{Y_t}). $$

Since $\sup_{t\in[0,T]}\mathbb {E}[Y_{t}^{p}]<\infty$ for any p>1 by Lemma C.2, Hölder’s inequality implies that it is sufficient to show

$$ \int_0^T \mathbb {E}\bigl[|H_t|^q\bigr]^{\frac{1}{q}} \,\mathrm {d}{t} < \infty\quad \text{for some }q>2,\ \text{where }H_t := X_t^{1-\gamma}g(t,Y_t)^k. $$

(C.12)

By (C.2), we have $|g(t,y)| \le\mathrm{e}^{\left \|{A}\right \|}(T-t)$. Therefore

$$|H_t| \le\mathrm{e}^{k\left \|{A}\right \|} X_t^{1-\gamma} (T-t)^k,\quad t\in[0,T]. $$

On the other hand, the admissibility condition (M′) implies that

$$\mathbb {E}\bigl[X_t^{q(1-\gamma)}\bigr]\le K(T-t)^{q(1-\gamma)} $$

if q−2 is sufficiently small. Therefore we obtain

$$\mathbb {E}\bigl[|H_t|^q\bigr]^{\frac{1}{q}} \le K (T-t)^{k+1-\gamma-1}\quad\text{for all }t\in[0,T] $$

for some K>0. By (H1), k+1−γ>−1. Consequently,

$${ \int_0^T} \mathbb {E}\bigl[H_t^q \bigr]^{\frac{1}{q}} \,\mathrm {d}{t} \le K{ \int_0^T} (T-t)^{k+1-\gamma} \,\mathrm {d}{t} < \infty $$

and thus (C.6) holds. This completes the proof. □

The following consequence of Lemma C.2 will be required in the proof of Proposition C.6.

Corollary C.7

If |π _t |≤K _π for all t∈[0,T], then the Novikov condition

$$\mathbb {E}\biggl[ \exp\biggl\{ \frac{1}{2}q^2(1- \gamma)^2 \int_0^T \pi_t^2Y_t\,\mathrm {d}{t} \biggr\} \biggr] < \infty $$

is satisfied for some q>2.

Proof

The claim follows immediately from Lemma C.2 and assumption (H3). □

The next result provides a crucial upper bound for the candidate optimal consumption–wealth ratio C ^⋆. Note that C ^⋆(t,y) increases linearly in y.

Lemma C.8

(Upper bound for consumption–wealth ratio)

We have

$$C^{\star}(t,y) \le\frac{1}{T-t} + b y + \frac{1}{2} \vartheta b(T-t)^2\quad\text{\textit{for all}}\ t\in[0,T],\ y\in [0,\infty). $$

Proof

Let τ>0 be arbitrary and consider the auxiliary function

$$h:\ [0,\infty)\to \mathbf {R},\quad h(x):=\frac{x}{1-\mathrm {e}^{-x\tau}}, $$

where $h(0):=\frac{1}{\tau}$. Then h is continuous and a straightforward calculation shows that h′(x)≤1 for all x>0. Thus the mean value theorem yields

$$ h(x) \le\frac{1}{\tau} + x\quad\text{for all}\ x\in[0, \infty). $$

(C.13)

Using (C.3) and (C.4), we then obtain

Now (C.7) implies

$$\frac{1}{\int_t^T \mathrm{e}^{A(t,s)-B(t,s)y}\mathrm {d}{s}} \le\frac {1}{T-t} + by +\frac{1}{2}\vartheta b(T-t)\quad\text{for all }t\in [0,T],\ y\in[0,\infty), $$

and the claim follows. □

We are now in a position to establish the second main result of this appendix.

Proposition C.9

(Sufficient conditions for admissibility in the Heston model)

Suppose the assumptions of Theorem 5.1 hold. Let (π,c) be a consumption-portfolio strategy and denote by C={C _t } the associated consumption–wealth ratio. If for some constant K>0 we have

$$ |\pi_t|\le K_\pi\ \text{\textit{and}}\ C_t\le\frac{1}{T-t} + b Y_t + K\quad\text{\textit{for all}}\ t\in[0,T], $$

(C.14)

then (π,c) satisfies the admissibility condition (M′). In particular, the strategy (π ^⋆,c ^⋆) in (5.2) is admissible.

Proof

The proof is divided into three steps. In the following, we denote by K a sufficiently large constant K>0 and by q a constant q>2. The precise magnitude of these constants may depend on the parameters of the model, but is independent of both y=Y _t and t.

Step 1: Change of measure. The investor’s wealth dynamics satisfy

$$\mathrm {d}{X}_t = X_t \bigl[(r+\pi_t\bar{\lambda}Y_t-C_t)\,\mathrm {d}{t}+\pi _t\sqrt{Y_t}\mathrm {d}{W}_t\bigr],\qquad X_0=x, $$

so $X_{t}^{1-\gamma}$ can be computed explicitly as

It follows that

$$X_t^{q(1-\gamma)} \le K \exp\bigg\{ q(\gamma-1){ \int_0^t} \varPsi_s \,\mathrm {d}{s} \bigg\} Z_t, $$

where the processes Z={Z _t } and Ψ={Ψ _t } are given by

(C.15)

By Novikov’s condition and Corollary C.4, Z={Z _t } is a martingale. Hence, under the equivalent measure $\tilde {\mathbb {P}}$ given by $\frac{\mathrm {d}\tilde {\mathbb {P}}}{\mathrm {d}\mathbb {P}} = Z_{t}$ on $\mathfrak {F}_{t}$, the process $\tilde {W}=\{\tilde{W}_{t}\}$ defined by

$$\tilde{W}_t := W_t - q(1-\gamma)\int_0^t\pi_s\sqrt{Y_s}\,\mathrm {d}{s} $$

is a standard Wiener process. With $\tilde {\mathbb {E}}$ denoting the expectation operator associated to $\tilde {\mathbb {P}}$, we thus have

$$ \mathbb {E}\bigl[X_t^{q(1-\gamma)}\bigr] \le K\ \tilde {\mathbb {E}}\bigg[ \exp\bigg\{ q(\gamma -1)\int_0^t \varPsi_s \,\mathrm {d}{s}\bigg\} \bigg]. $$

(C.16)

Step 2: Dynamics of Y under $\tilde {\mathbb {P}}$. Observe that Y has the $\tilde {\mathbb {P}}$-dynamics

$$\mathrm {d}{Y}_t=(\vartheta- \tilde{\kappa }_t Y_t)\,\mathrm {d}{t} + \bar{\beta }\sqrt{Y_t}\big( \rho\,\mathrm {d}\tilde{W}_t+\sqrt{1-\rho^2}\,\mathrm {d}\hat {W}_t \big), $$

where $\tilde{W}$ and $\hat{W}$ are independent standard $\tilde {\mathbb {P}}$-Wiener processes and

$$\tilde{\kappa }_t := \kappa - q(1-\gamma)\bar{\beta}\rho\pi_t = \kappa + q(\gamma-1)\bar{\beta}|\rho|\pi_t\quad\text{for }t\in[0,T]. $$

Assumption (H3) implies that

$$\underline{\kappa } := \kappa - q(\gamma-1)\bar{\beta} K_\pi> 0, $$

provided q−2 is sufficiently small. By (C.8), we have $\tilde{\kappa }_{t}\ge\underline {\kappa }$. It follows that $\vartheta-\tilde{\kappa }_{t} y\le \vartheta-\underline{\kappa }y$ for all t∈[0,T] and y∈[0,∞). Thus, by a ramification of a classical comparison result of Yamada and Watanabe, see e.g. Theorem V.43.1 in [26],

$$ Y_t \le\tilde{Y}_t\quad\text{for all }t\in[0,T], $$

(C.17)

where $\tilde{Y}=\{\tilde{Y}_{t}\}$ follows a square-root process

$$ \mathrm {d}\tilde{Y}_t = (\vartheta- \underline{\kappa }\tilde{Y}_t)\,\mathrm {d}{t} + \bar{\beta}\sqrt{\tilde{Y}_t}\big( \rho\,\mathrm {d}\tilde{W}_t+\sqrt{1- \rho^2}\,\mathrm {d}\hat{W}_t \big),\qquad\tilde{Y}_0=Y_0. $$

(C.18)

Step 3: Verification of (M′). The quantity Ψ _t defined before (C.9) can be interpreted as a convex parabola in π=π _t with vertex at π=0. Therefore,

$$\varPsi_t \le C_t + \frac{1-q+q\gamma}{2} K_\pi^2 Y_t, $$

and in combination with the assumption (C.8) on C _t , we obtain

$$\varPsi_t \le\frac{1}{T-t} + \tilde{b}_q Y_t + K\quad\text{for all}\ t\in[0,T],\ y\in[0,\infty), $$

where $\tilde{b}_{q} := b + \frac{1-q+q\gamma}{2} K_{\pi}^{2}$. Hence, by (C.10), we get

where the third line follows from (C.11). Now, by (C.12), $\tilde{Y}$ is a square-root process under $\tilde {\mathbb {P}}$, and assumption (H3) ensures that

$$q(\gamma-1)\tilde{b}_q \le\frac{\underline{\kappa }^2}{2\bar{\beta}^2} $$

if q−2 is sufficiently small.¹⁶ Hence Lemma C.2 yields

$$\sup\limits_{t\in[0,T]} \tilde {\mathbb {E}}\bigg[\exp\bigg\{ q(\gamma -1)\tilde{b}_q \int_0^t \tilde{Y}_s \,\mathrm {d}{s} \bigg\} \bigg] \le K < \infty $$

and thus

$$\mathbb {E}\bigl[X_t^{q(1-\gamma)}\bigr] \le K (T-t)^{-q(\gamma-1)}\quad\text{for all}\ t\in[0,T]. $$

Consequently (M′) is satisfied with ℓ=q(γ−1)>2(γ−1). The last part of the assertion follows immediately from (C.5) and Lemma C.5. □

Remark

Note that Proposition C.6 implies in particular that there exists a continuation value process $V^{\star}=\{V^{\star}_{t}\}$ corresponding to (π ^⋆,c ^⋆); see the discussion following Theorem 3.1. In fact, we have $V^{\star}_{t}=w(t,X^{\star}_{t},Y_{t})$ for t∈[0,T].

Appendix D: Proofs of Propositions 5.2 and 5.3

Proof of Proposition 5.2

Since the PDEs (4.5) for g in the Heston and the inverse Heston model are identical, the claim follows from the first part of the proof of Theorem 5.1. □

Proof of Proposition 5.3

Note that in terms of the notation of Sect. 5.2,

$$\tilde{r}(y) = -{1}{k}\bigg[r(1-\gamma)-\delta\theta+\frac {1}{2}\frac{1-\gamma}{\gamma}y^2\bigg],\qquad\tilde{\alpha}(y) = \vartheta-\bigg(\kappa -\frac{1-\gamma}{\gamma}\beta\rho\bigg)y, $$

and as in the first part of the proof of Theorem 5.1, it suffices to solve (4.6). The conjecture $h(t,y;s)=\mathrm {e}^{A(t,s)-B(t,s)y-C(t,s)y^{2}}$, (t,y)∈[0,s]×R, yields for $A(\:\cdot \:,s)$, $B(\:\cdot \:,s)$ and $C(\:\cdot \:,s)$ the ODEs

Therefore,

(D.19)

where $\hat{\kappa } := \kappa -\frac{1-\gamma}{\gamma}\beta\rho$, $b := -\frac{1}{2}\frac{1-\gamma}{k\gamma}$ and $a := 2\sqrt{\hat{\kappa }^{2}+2b\beta^{2}}$. The function $A(\:\cdot \:,s)$ can then be found by integrating the corresponding trivial ODE. □