Optimal consumption and investment with Epstein–Zin recursive utility

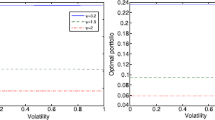
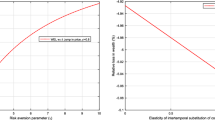
Abstract

We study continuous-time optimal consumption and investment with Epstein–Zin recursive preferences in incomplete markets. We develop a novel approach that rigorously constructs the solution of the associated Hamilton–Jacobi–Bellman equation by a fixed point argument and makes it possible to compute both the indirect utility and, more importantly, optimal strategies. Based on these results, we also establish a fast and accurate method for numerical computations. Our setting is not restricted to affine asset price dynamics; we only require boundedness of the underlying model coefficients.

Appendices

Appendix A: Proofs omitted from the main text

Proof of Lemma 4.6

Since $h$ solves the reduced HJB equation (4.7), we have

$$\begin{aligned} H(z, \hat{\pi}, \hat{c}) :=& w_{t} + x(r + \hat{\pi}\lambda) w_{x} - \hat{c}w_{x} + \frac{1}{2} x^{2} \hat{\pi}^{2} \sigma ^{2} w_{xx} + \alpha w_{y} \\ &{} + \frac{1}{2} \beta^{2} w_{yy} + x \hat{\pi}\sigma \beta \rho w_{xy} + f(\hat{c},w) = 0, \end{aligned}$$

where $z:=(t,x,y, w_{x}, w_{y}, w_{x_{y}} w_{xx}, w_{yy})$. Separating the terms in the function $H$ as $H(z, \pi ,c) :=u(z, \pi) + s(z, c) + q(z)$, it is easy to see that the candidate solutions $\hat{\pi}$ and $\hat{c}$ defined in (4.6) are the unique solutions of the associated first-order conditions

$$\begin{aligned} \begin{aligned} 0&= s_{c}(z, c) = -w_{x} + f_{c}(c, w),\\ 0&= u_{\pi}(z, \pi) =x \lambda w_{x} + \pi x^{2} \sigma ^{2} w_{xx} + x \sigma \beta \rho w_{xy}. \end{aligned} \end{aligned}$$

(A.1)

Concavity of $u$ and $s$ implies that $H(z, \hat{\pi}, \hat{c}) = { \sup_{\pi\in \mathbb{R},\, c\in(0,\infty)}} H(z, \pi ,c)$. □

Proof of Lemma 4.7

By (A1) and (A2), $\tilde{\alpha}$ and $\tilde{r}$ are bounded. Moreover,

$$\begin{aligned} |\tilde{\alpha}(y) - \tilde{\alpha}(\bar{y})| \leq& \bigg|\frac {1-\gamma}{\gamma}\bigg| \rho \bigg(\bigg|\frac{\lambda(y)}{\sigma(y)} \bigg| |\beta(y) -\beta(\bar{y})| + \bigg|\frac {\beta(\bar{y})}{\sigma(y)}\bigg| | {\lambda (y)} - {\lambda(\bar{y})} |\bigg)\\ &{}+ |\beta(\bar{y}) \lambda(\bar{y})| \bigg| \frac {\sigma (\bar{y}) -\sigma(y)}{\sigma(y)\sigma(\bar{y})}\bigg| + |\alpha (y) - \alpha(\bar{y})| \end{aligned}$$

so that $\tilde{\alpha}$ is Lipschitz-continuous. Finally,

$$\begin{aligned} k|\tilde{r}(y) -\tilde{r}(\bar{y})| \leq& |1-\gamma| |r(y)-r(\bar{y})| \\ &{}+ \bigg|\frac {1-\gamma}{\gamma}\bigg| \|\lambda\|_{\infty}\Big(\inf_{x \in \mathbb{R}} \sigma(x)\Big)^{-2} |\lambda(y) - \lambda(\bar{y})|\\ &{}+ \bigg|\frac {1-\gamma}{\gamma}\bigg| \|\lambda\|_{\infty}^{2} \|\sigma\|_{\infty}\Big(\inf_{x \in \mathbb{R}} \sigma(x)\Big)^{-4} |\sigma(\bar{y}) -\sigma (y)|. \end{aligned}$$

 □

Proof of Lemma 5.3

The candidate optimal wealth process $\hat{X}$ has dynamics

$$\mathrm{d} \hat{X}_{t} = \hat{X}_{t}\bigg( \Big(r_{t} + \frac{1}{\gamma}\frac{\lambda_{t}^{2}}{\sigma_{t}^{2}} + \frac{k}{\gamma}\frac {\lambda_{t} \beta_{t} \rho}{\sigma_{t}} \frac{h_{y}}{h} - \delta^{\psi}h^{q-1}\Big)\,\mathrm{d} t + \Big(\frac{1}{\gamma}\frac{\lambda_{t}}{\sigma_{t}} + \frac{k}{\gamma}\beta_{t} \rho \frac{h_{y}}{h}\Big) \,\mathrm{d} W_{t}\bigg). $$

Put $a_{t}:=r_{t} + \frac{1}{\gamma}\frac{\lambda_{t}^{2}}{\sigma_{t}^{2}}+ \frac{k}{\gamma}\frac{\lambda_{t}\beta_{t} \rho}{\sigma_{t}} \frac{h_{y}}{h} - \delta^{\psi}h^{q-1}$ and $b_{t}:=\frac{1}{\gamma}\frac{\lambda_{t}}{\sigma_{t}} + \frac{k}{\gamma}\beta_{t} \rho \frac {h_{y}}{h}$. Our assumptions on the coefficients and on $h_{y}$ and $h$ imply that both $a$ and $b$ are bounded. By Itô’s formula,

$$\hat{X}_{t}^{p} = x^{p} \, \exp\bigg(p{ \int_{0}^{t}} \Big(a_{s} + \frac{1}{2} (p-1) b_{s}^{2} \Big) \,\mathrm{d} s \bigg) {\mathcal {E}}_{t} \bigg(p{ \int_{0}^{{\,\cdot \,}}} b_{s} \,\mathrm{d} W_{s} \bigg), $$

where $\mathcal {E}_{t}({\,\cdot \,})$ denotes the stochastic exponential. Choose the constant $M>0$ such that $|p a_{t}| + |p(p-1) b_{t}^{2}|, |p b_{t}| < M$ for all $t\in[0,T]$. By Novikov’s condition, ${\mathcal {E}}_{t} (p\int_{0}^{{\,\cdot \,}}b_{s} \,\mathrm{d} W_{s} )$ is then an $L^{2}$-martingale; so using Doob’s $L^{2}$-inequality, we get

$$\operatorname{E}\bigg[{ \sup _{t \in [0,T]}} \hat{X}_{t}^{p}\bigg] \leq 2 x^{p} e^{M T} \operatorname{E}\bigg[{\mathcal {E}}_{T} \left(p{ \int_{0}^{{\,\cdot \,}}} b_{s} \,\mathrm{d} W_{s} \right)^{2} \bigg]^{\frac{1}{2}} < \infty. $$

 □

Proof of Lemma 5.4

Lemma 5.3 and the boundedness of $\delta^{\psi}h(t,Y_{t})^{q-1}$ imply that $\operatorname{E}[ {\sup_{t\in[0,T]}} |\hat{c}_{t}|^{p} ] < \infty$ for all $p \in \mathbb{R}$. In particular, $\hat{c}$ is in $\mathcal{C}$. By Itô’s formula,

$$\begin{aligned} \mathrm{d} V_{t} = \bigg(&w_{t}+ \hat{X}_{t}(r_{t} + \hat{\pi}_{t} \lambda_{t}) w_{x} - \hat{c}_{t}w_{x} + \frac{1}{2} \hat{X}_{t}^{2} \hat{\pi}_{t}^{2} \sigma_{t} ^{2} w_{xx} + \alpha_{t} w_{y} + \frac{1}{2} \beta_{t}^{2} w_{yy} \\ &{}+ \hat{X}_{t} \hat{\pi}_{t} \sigma_{t} \beta_{t} \rho w_{xy} \bigg) \,\mathrm{d} t + \,\mathrm{d} M_{t}, \end{aligned}$$

where $M$ is a local martingale. Hence $\mathrm{d} V_{t} = - f(\hat{c}_{t}, V_{t}) \,\mathrm{d} t + \,\mathrm{d} M_{t}$ by Lemma 4.6. Moreover, exploiting the special form of $w$, we get

$$\mathrm{d} M_{t}= V_{t}\bigg( \frac{1-\gamma}{\gamma}\frac{\lambda_{t}}{\sigma_{t}} + \frac{\rho k}{\gamma}\beta_{t} \frac{h_{y}}{h} \bigg) \,\mathrm{d} W_{t} + V_{t} k \sqrt{1-\rho^{2}} \beta_{t}\frac{h_{y}}{h} \,\mathrm{d} \bar{W}_{t}. $$

Here $V_{t}$ can be rewritten as $V_{t} = w(t, \hat{X}_{t}, Y_{t}) = \frac{1}{1-\gamma} \hat{X}_{t}^{1-\gamma} h(t,Y_{t})^{k}$. By (4.8), the function $h$ is bounded and bounded away from zero. Thus we have for all $p \in \mathbb{R}$ by Lemma 5.3 that $\operatorname{E}[{\sup_{t\in[0,T]}} |V_{t}|^{p} ] <\infty$. Hence $V$ is a utility process associated with $\hat{c}$; by (E1), it follows that $V=V^{\hat{c}}$. Finally, the first-order condition (A.1) for the optimal consumption implies that $w_{x}(t, \hat{X}_{t}, Y_{t}) = f_{c}(t, w(t, \hat{X}_{t}, Y_{t})) = f_{c}(\hat{c}_{t}, \hat{V}_{t})$. □

Proof of Lemma 5.5

For simplicity of notation, we set $r_{t}:=r(Y_{t})$, $\lambda_{t}:=\lambda(Y_{t})$ and $\sigma_{t}:=\sigma(Y_{t})$. We have $\mathrm{d} Z^{\pi, c}_{t} = \hat{m}_{t} c_{t} \,\mathrm{d} t + \hat{m}_{t} \,\mathrm{d} X_{t}^{\pi,c} + X_{t}^{\pi ,c} \,\mathrm{d} \hat{m}_{t} + \,\mathrm{d} [\hat{m},X^{\pi,c}]_{t}$ by the product rule. Inserting the dynamics of $X^{\pi ,c}$ from (4.1), we get

$$ \mathrm{d} Z^{\pi, c}_{t} = \hat{m}_{t} X_{t}^{\pi ,c}\big((r_{t} + \pi_{t} \lambda_{t}) \,\mathrm{d} t + \pi_{t} \sigma _{t} \,\mathrm{d} W_{t}\big) + X_{t}^{\pi ,c} \,\mathrm{d} \hat{m}_{t} + \,\mathrm{d} [ \hat{m}, X^{\pi ,c }]_{t}. $$

By Lemma 5.4, $\hat{V}_{t}=w(t,\hat{X}_{t},Y_{t})$ and $\hat{m}_{t} = e^{\int_{0}^{t} f_{v}(\hat{c}_{s}, \hat{V}_{s}) \,\mathrm{d} s} w_{x}(t,\hat{X}_{t},Y_{t})$. From here on, we abbreviate $f_{v} = f_{v}(\hat{c}_{t}, \hat{V}_{t})$, $w_{x} = w_{x}(t, \hat{X}_{t}, Y_{t})$ etc. Clearly, we have $\mathrm{d} \hat{m}_{t} = \hat{m}_{t} ( f_{v} \,\mathrm{d} t + \frac{\mathrm{d} w_{x}}{w_{x}} )$.

From the explicit expression $f_{v}(c, v) = \delta \frac {\phi -\gamma}{1-\phi} c^{1 -\phi} ((1-\gamma)v)^{\frac{\phi-1}{1-\gamma}} - \delta \theta$, we obtain $f_{v}(\hat{c}_{t}, w(t, \hat{X}_{t}, Y_{t}))= \frac{\phi-\gamma}{1-\phi} \delta^{\psi} h^{q -1} - \delta\theta$. By Itô’s formula,

$$\mathrm{d} w_{x} = w_{x} \bigg(\frac {w_{xt} }{w_{x}} \,\mathrm{d} t + \frac {w_{xx} }{w_{x}} \,\mathrm{d} \hat{X}_{t} + \frac{1}{2} \frac {w_{xxx} }{w_{x}} \,\mathrm{d} [\hat{X}]_{t} + \frac{1}{2} \frac {w_{xyy} }{w_{x}} \,\mathrm{d} [Y]_{t} + \frac {w_{xxy} }{w_{x}} \,\mathrm{d} [\hat{X}, Y]_{t} \bigg). $$

Substituting for $w$, we find

$$\begin{aligned} \frac {\mathrm{d} w_{x}}{k w_{x}} =& \frac {h_{t}}{h} \,\mathrm{d} t -\frac{\gamma}{k} \frac {\,\mathrm{d} \hat{X}_{t} }{\hat{X}_{t}} + \frac {h_{y}}{h} \,\mathrm{d} Y_{t} + \frac{1}{2} \frac {\gamma (1+ \gamma)}{k} \frac {\,\mathrm{d} [\hat{X}]_{t}}{\hat{X}_{t}^{2}}\\ &{} +\frac{1}{2} \bigg((k-1) \frac {h_{y}^{2}}{h^{2}} + \frac {h_{yy}}{h} \bigg)\,\mathrm{d} [Y]_{t} - \frac{\gamma}{\hat{X}_{t}} \frac {h_{y}}{h} \,\mathrm{d} [\hat{X}, Y]_{t}. \end{aligned}$$

Plugging in the candidate $\hat{\pi}$ from (5.1) and the dynamics of $\hat{X}$ and $Y$ yields

$$\frac{\mathrm{d} w_{x}}{k w_{x}} = A^{1}_{t} \,\mathrm{d} t + A^{2}_{t} \,\mathrm{d} t - \frac{1}{k} \frac {\lambda_{t}}{\sigma _{t}} \,\mathrm{d} W_{t} + \sqrt{1- \rho^{2}}\beta_{t} \frac {h_{y}}{h} \,\mathrm{d} \bar{W}_{t}, $$

where

$$\begin{aligned} A_{t}^{1} &:=\frac {h_{t}}{h} -\frac{\gamma}{k} r_{t} + \frac{1}{2} \frac{1}{k} \frac {1- \gamma}{\gamma}\frac {\lambda_{t}^{2}}{\sigma_{t}^{2}} + \frac{1}{\gamma}\frac {\lambda_{t} \beta_{t} \rho}{\sigma}\frac {h_{y}}{h} + \frac{\gamma}{k} \delta^{\psi}h^{q-1} + \frac{k}{2} \frac {1+ \gamma}{\gamma}\beta_{t}^{2} \rho^{2} \frac{h_{y}^{2}}{h^{2}},\\ A_{t}^{2} &:=\frac {h_{y}}{h} \bigg( \alpha_{t} - \frac{\rho \beta_{t} \lambda_{t}}{\sigma_{t}}\bigg) + \frac {h_{y}^{2} }{h^{2}} \left( \frac {k-1}{2} \beta_{t}^{2} - k \beta_{t}^{2} \rho^{2} \right) + \frac {\beta_{t}^{2}}{2} \frac {h_{yy}}{h}. \end{aligned}$$

For the sum of the $\frac {h_{y}^{2}}{h^{2}}$-terms, we have

$$\frac{k}{2} \frac {1+ \gamma}{\gamma}\beta_{t}^{2} \rho^{2} \frac{h_{y}^{2}}{h^{2}} + \frac {h_{y}^{2} }{h^{2}} \bigg( \frac {k-1}{2} \beta_{t}^{2} - k \beta_{t}^{2} \rho^{2}\! \bigg) = \beta_{t}^{2} \frac{h_{y}^{2}}{h^{2}} \bigg( \frac{k}{2} \rho ^{2} \frac {1+ \gamma}{\gamma}+ \frac {k-1}{2} - \rho^{2} k \bigg) = 0 $$

by our choice of $k$. Combining the above, we obtain

$$\begin{aligned} \mathrm{d} \hat{m}_{t} =& k \hat{m}_{t} \bigg(\frac {h_{t}}{h} + \frac{1}{k} \Big( -\gamma r_{t} + \frac{1}{2} \frac {1- \gamma}{\gamma}\frac {\lambda_{t} ^{2}}{\sigma_{t}^{2}} - \delta \theta \Big) \\ &\quad\ \quad{}+ \tilde{\alpha}_{t} \frac {h_{y}}{h} + \frac {\beta_{t}^{2}}{2} \frac {h_{yy}}{h} + \frac {\phi \theta}{k} \delta ^{\psi}h^{q-1} \bigg)\\ &{}+ k \hat{m}_{t} \bigg(- \frac{1}{k} \frac {\lambda_{t}}{\sigma _{t}} \,\mathrm{d} W_{t} + \sqrt{1- \rho^{2}}\beta_{t} \frac {h_{y}}{h} \,\mathrm{d} \bar{W}_{t} \bigg), \end{aligned}$$

and it follows that $\mathrm{d} [\hat{m}, X^{\pi , c}]_{t} = - \lambda_{t} \pi_{t} \hat{m}_{t} X_{t}^{\pi,c} \,\mathrm{d} t$. Since $h$ solves (4.7), we get

$$\begin{aligned} \mathrm{d} Z^{\pi, c}_{t} &= \hat{m}_{t} X_{t}^{\pi ,c}\big((r_{t} + \pi_{t} \lambda_{t}) \,\mathrm{d} t + \pi_{t} \sigma _{t} \,\mathrm{d} W_{t}\big) + X_{t}^{\pi ,c} \,\mathrm{d} \hat{m}_{t} + \,\mathrm{d} [ \hat{m}, X^{\pi ,c }]_{t}\\ &= \hat{m}_{t} X_{t}^{\pi ,c} \frac{1}{h} \bigg({h_{t}} - \tilde{r}_{t} h + \tilde{\alpha}_{t} {h_{y}} + \frac{1}{2}\beta_{t}^{2} h_{yy} + \frac{\delta^{\psi}}{1-q} h^{q} \bigg) \,\mathrm{d} t + \,\mathrm{d} M_{t} = \,\mathrm{d} M_{t}, \end{aligned}$$

where $\mathrm{d} M_{t}:=\hat{m}_{t} X_{t}^{\pi,c} ((\pi_{t} \sigma_{t} - \frac {\lambda_{t}}{\sigma _{t}} ) \,\mathrm{d} W_{t} + k\sqrt{1- \rho^{2}}\beta_{t} \frac {h_{y}}{h} \,\mathrm{d} \bar{W}_{t} )$ defines a local martingale $M$. A direct calculation using the definition of $\hat{\pi}$ yields the statement for $Z^{\hat{\pi}, \hat{c}}$. □

Proof of Lemma 5.6

Recall that $\underline{h}\leq h\leq \overline{h}$ so that

$$f_{v}(\hat{c}_{s},\hat{V}_{s}) = \frac{\phi-\gamma}{1-\phi} \delta^{\psi} h(s,Y_{s})^{q-1} - \delta\theta \leq \bigg|\frac{\phi-\gamma}{1-\phi}\bigg| \delta^{\psi} \left( \underline{h}^{q-1} + \overline{h}^{q-1}\right) + |\delta\theta| =: m_{1} $$

and we get $0 \leq \exp(p{\int_{0}^{T}} f_{v}(\hat{c}_{s}, \hat{V}_{s}) \,\mathrm{d} s ) \leq e^{Tp m_{1}}$. On the other hand, Lemma 5.4 implies that $\operatorname{E}[{\sup_{t \in [0,T]}} f_{c}(\hat{c}_{t}, \hat{V}_{t})^{p}] < \infty$ for all $p \in \mathbb{R}$. It follows that

$$\operatorname{E}\bigg[ { \sup_{t\in[0,T]}} \hat{m}_{t}^{p} \bigg] < \infty\quad\text{for all }p>1. $$

To show that $Z^{\hat{\pi}, \hat{c}}$ is a martingale, note that $\frac {1- \gamma}{\gamma}\frac {\lambda_{t}}{\sigma_{t}} + \frac{k}{\gamma}\beta_{t} \rho \frac {h_{y}}{h}$ is uniformly bounded by some $c>0$. Hence by Lemma 5.3, we have

$${\int_{0}^{T}} \operatorname{E}\bigg[\hat{m}_{t}^{2} \hat{X}_{t}^{2} \bigg(\frac{1- \gamma}{\gamma}\frac {\lambda_{t}}{\sigma_{t}} + \frac{k}{\gamma}\beta_{t} \rho \frac {h_{y}}{h}\bigg)^{2} \bigg] \,\mathrm{d} t \leq c^{2} { \int_{0}^{T}} \sqrt {\operatorname{E}[\hat{m}_{t}^{4}] \operatorname{E}[\hat{X}_{t}^{4}] } \,\mathrm{d} t< \infty. $$

Analogously, we obtain that $\int_{0}^{T} \operatorname{E}[ \hat{m}_{t}^{2} \hat{X}_{t}^{2} (k\sqrt{1- \rho^{2}}\beta_{t} \frac {h_{y}}{h})^{2}] \,\mathrm{d} t <\infty$. From this and Lemma 5.5, we conclude that $Z^{\hat{\pi},\hat{c}}$ is an $L^{2}$-martingale. □

Proof of Proposition 6.4

For any fixed $\kappa > c + \varrho$, define a metric $d$ equivalent to $\|{\,\cdot \,}\|_{\infty}$ by $d(X,Y):=\mathop {\mathrm {ess}\,\mathrm {sup}}_{\,\mathrm{d} t \otimes \,\mathrm{d} \mathrm{P}} e^{-\kappa (T-t)} |X_{t} - Y_{t}|$. Then $(A,d)$ is a complete metric space. By definition, $|X_{s}-Y_{s}| \leq e^{\kappa (T-s)} d(X,Y) \,\mathrm{d} t \otimes \,\mathrm{d}\mathrm{P}$-a.e., so

$$\begin{aligned} e^{-\kappa (T-t)} |(S X)_{t} - (S Y)_{t} | &\leq e^{-\kappa (T-t)} c { \int_{t}^{T}} e^{(s-t)\varrho} e^{\kappa (T-s)} d(X,Y) \,\mathrm{d} s\\ &\leq \frac {c}{\kappa- \varrho } d(X,Y), \end{aligned}$$

and we conclude that $d(SX,SY) \leq \frac {c}{\kappa- \varrho} d(X,Y)$, where $\frac {c}{\kappa- \varrho}<1$. Hence $S$ is a contraction on $(A,d)$. Thus by Banach’s fixed point theorem, there is a unique $X\in A$ with $S X = X$, and we have $d(X_{(n)},X) \leq ( \frac {c}{\kappa-\varrho})^{n} d(X_{(0)},X)$ for all $n\in \mathbb{N}$. Hence it follows that

$$\begin{aligned} |(X_{(n)})_{t} - X_{t}|&\leq e^{\kappa T} d(X_{(n)},X) \leq \bigg(\frac{c}{\kappa-\varrho}\bigg)^{n} e^{\kappa T} d(X_{(0)},X)\\ &\leq e^{\kappa T} \big(\|X_{(0)}\|_{\infty}+ \|X\|_{\infty}\big) \bigg(\frac{c}{\kappa-\varrho}\bigg)^{n} \end{aligned}$$

and thus $\|X_{(n)}-X\|_{\infty}\le e^{\kappa T} (\|X_{(0)}\|_{\infty}+ \|X\|_{\infty}) (\frac {c}{\kappa - \varrho} )^{n}$, for every $n\in \mathbb{N}$ and every choice of $\kappa>c+\varrho$. Setting $\kappa=\frac{n+T\varrho}{T}$ for $n>cT$, we obtain the asserted error bound. □

Appendix B: Stochastic Gronwall inequality

This appendix provides a ramification of the stochastic Gronwall–Bellman inequality which is required for the proofs in this article. Related results can be found in [17, 1, 36]. We work on a general probability space $(\varOmega, \mathcal {F},\mathrm{P})$ that is endowed with a filtration $(\mathcal {F}_{t})_{t \geq 0}$ that is right-continuous and complete.

Proposition B.1

Suppose $A=(A_{t})_{t\in[0,T]}$ is bounded and progressively measurable, $Z \in L^{p}(\mathrm{P})$ and $B=(B_{t})_{t\in[0,T]}$ is a progressively measurable process in $L^{p}(\,\mathrm{d} t \otimes \,\mathrm{d}\mathrm{P})$ for some $p>1$. Moreover, let $X = (X_{t})_{t \in [0,T]}$ be right-continuous and adapted with $\operatorname{E}[\sup_{t\in [0,T]} |X_{t}|]<\infty$. If

$$ 1_{\{\tau > t\}} X_{t} \geq \operatorname{E}_{t}\left[ 1_{\{\tau > t\}} { \int _{t}^{\tau}} \left(A_{s} X_{s}+ B_{s} \right) \,\mathrm{d} s + 1_{\{\tau > t\}}X_{\tau}\right] \quad \textit{a.s. for }t \in [0,T] $$

(B.1)

for every stopping time $\tau$ and $X_{T} \geq Z$, then

$$X_{t} \geq \operatorname{E}_{t} \left[{ \int_{t}^{T}} e^{\int_{t}^{s} A_{u} \,\mathrm{d} u} B_{s} \,\mathrm{d} s + e^{\int_{t}^{T} A_{s} \,\mathrm{d} s} Z \right] \quad \textit{for all } t \in [0,T]\ \textit{a.s.} $$

Proof

We set

$$M_{t}:=\operatorname{E}_{t} \left[{ \int_{0}^{T}} e^{\int_{0}^{s} A_{u} \,\mathrm{d} u} B_{s} \,\mathrm{d} s + e^{ \int_{0}^{T} A_{s} \,\mathrm{d} s}Z\right]. $$

Since $A$ is bounded above, $Z\in L^{p}(\mathrm{P})$ and $B \in L^{p}(\,\mathrm{d} t \otimes \,\mathrm{d}\mathrm{P})$, it follows from Doob’s $L^{p}$-inequality that $\operatorname{E}[\sup_{t\in [0,T]} |M_{t}|^{p}]<\infty$. In particular, $M$ is well defined as a uniformly integrable martingale. Now set

$$Y_{t}:=e^{- \int_{0}^{t} A_{s} \,\mathrm{d} s} \left(M_{t} - { \int_{0}^{t}} e^{\int_{0}^{s} A_{u} \,\mathrm{d} u} B_{s} \,\mathrm{d} s \right). $$

Since $A$ is bounded below, we have $\operatorname{E}[\sup_{t\in[0,T]}|Y_{t}|^{p}]<\infty$, and integration by parts yields

$$ \mathrm{d} Y_{t} = e^{-\int_{0}^{t} A_{s} \,\mathrm{d} s}\big(\,\mathrm{d} M_{t} - e^{\int_{0}^{t} A_{u} \,\mathrm{d} u} B_{t} \,\mathrm{d} t \big) - Y_{t-} A_{t} \,\mathrm{d} t = -(A_{t} Y_{t} + B_{t} ) \,\mathrm{d} t + \,\mathrm{d} N_{t}, $$

where $N_{t}:=\int_{0}^{t} e^{-\int_{0}^{s} A_{u}\,\mathrm{d} u}\,\mathrm{d} M_{s}$ is a uniformly integrable martingale. For an arbitrary stopping time $\tau$, we obtain

$$Y_{t} - Y_{\tau}= -{ \int_{0}^{t}} (A_{s}Y_{s} + B_{s}) \,\mathrm{d} s + N_{t} + { \int_{0}^{\tau}} (A_{s} Y_{s} + B_{s})\,\mathrm{d} s - N_{\tau} \quad \text{on } \{\tau>t\}, $$

so that

$$ 1_{\{\tau >t \}} Y_{t} = 1_{\{\tau >t \}} { \int_{t}^{\tau}} (A_{s} Y_{s} + B_{s}) \,\mathrm{d} s + 1_{\{\tau >t \}}(N_{t} - N_{\tau}) + 1_{\{\tau >t \}} Y_{\tau}. $$

Since $(1_{\{\tau >t \}}(N_{t} - N_{\tau}))_{s\in[t,T]}$ is a martingale, it follows that

$$ 1_{\{\tau >t \}} Y_{t} = \operatorname{E}_{t} \left[1_{\{\tau >t \}} { \int_{t}^{\tau}} (A_{s} Y_{s} + B_{s}) \,\mathrm{d} s + 1_{\{\tau >t \}} Y_{\tau}\right]. $$

(B.2)

We set $\Delta_{t}:=X_{t} -Y_{t}$ and obtain $\Delta_{T} = X_{T}-Z \ge 0$ and $\operatorname{E}[\sup_{t\in[0,T]}|\Delta_{t}|]<\infty$. Moreover, (B.1) and (B.2) imply that for any stopping time $\tau$,

$$ 1_{\{\tau > t\}} \Delta_{t} \geq \operatorname{E}_{t}\left[ 1_{\{\tau > t\}} { \int _{t}^{\tau}} A_{s} \Delta_{s} \,\mathrm{d} s + 1_{\{\tau > t\}}\Delta_{\tau}\right] \quad \text{a.s. for all }t \in [0,T]. $$

Thus Proposition C.2 in [40] applies to yield $\Delta_{t} \geq 0$ for all $t\in[0,T]$ a.s., i.e.,

$$X_{t} \geq Y_{t} = e^{- \int_{0}^{t} A_{u} \,\mathrm{d} u} \operatorname{E}_{t} \left[ { \int_{t}^{T}}e^{\int_{0}^{s} A_{u} \,\mathrm{d} u} B_{s} \,\mathrm{d} s + e^{\int_{0}^{T} A_{s} \,\mathrm{d} s} Z \right]. $$

 □

Appendix C: Some facts on parabolic partial differential equations

This appendix collects the relevant results on linear and semilinear parabolic partial differential equations that are used in this article. Following [29], we first introduce the Hölder spaces $H^{r/2,r}([0,T] \times \mathbb{R}^{d})$ for $r\in \mathbb{R}_{+}$. For a continuous function $u: [0,T]\times \mathbb{R}^{d} \to \mathbb{R}, (t,x) \mapsto u(t,x)$, and $q\in(0,1)$, we define the Hölder coefficient $\langle u\rangle^{q}_{x}$ in space via

$$\langle u\rangle^{q}_{x} :=\sup_{t \in [0,T],\ x,x' \in \mathbb{R}^{d},\ |x-x'| \leq 1} \frac {|u(t,x) - u(t,x')|}{|x-x'|^{q}} $$

and the Hölder coefficient $\langle u\rangle^{q}_{t}$ in time via

$$\langle u\rangle^{q}_{t} :=\sup_{t,t' \in [0,T],\ x\in \mathbb{R}^{d},\ |t-t'| \leq 1} \frac {|u(t,x) - u(t,x')|}{|t-t'|^{q}}. $$

The space $H^{r/2,r}([0,T]\times \mathbb{R}^{d})$ consists of all functions $u: [0,T]\times \mathbb{R}^{d}\to \mathbb{R}$ that are continuous along with all derivatives $D^{\alpha}_{t} D^{\beta}_{x} u$ with “order” $2|\alpha| + |\beta| \le r$ and satisfy $\|u\|_{H}^{r/2,r} < \infty$. Here the norm $\|u\|_{H}^{r/2,r}$ of $u$ is given by

$$\|u\|_{H}^{r/2,r} :=\langle u \rangle^{r/2,r}_{\bullet}+ \sum_{2|\alpha| + |\beta|\leq \lfloor r \rfloor } \| D^{\alpha}_{t} D_{x}^{\beta}u\|_{\infty}, $$

where the mixed space-time Hölder coefficient $\langle u\rangle^{r/2,r}_{\bullet}$ of $u$ is given by

$$\langle u \rangle^{r/2,r}_{\bullet} :=\sum_{2|\alpha| + |\beta| = \lfloor r \rfloor } \langle D^{\alpha}_{t} D_{x}^{\beta}u \rangle^{r - \lfloor r \rfloor}_{x} + \sum_{r-2< 2|\alpha|+|\beta|< r} \langle D^{\alpha}_{t} D_{x}^{\beta}u \rangle^{\frac {r-2|\alpha|-|\beta|}{2}}_{t}. $$

Thus $\|u\|_{H}^{r/2,r}$ sums up the $L^{\infty}$-norms of all relevant derivatives plus the Hölder coefficients of the highest-order derivatives. Analogously, for $r\in \mathbb{R}_{+}$, the space $H^{r}(\mathbb{R}^{d})$ is defined as the collection of all $\lfloor r \rfloor$ times continuously differentiable functions $u: \mathbb{R}^{d} \to \mathbb{R}$ with $\|u\|_{H}^{r} < \infty$, where⁶

$$\|u\|_{H}^{r} :=\langle u\rangle^{r}_{\bullet}+ \sum_{|\beta| \leq \lfloor r \rfloor} \| D^{\beta}u \|_{\infty}\quad \text{and}\quad \langle u\rangle^{r}_{\bullet} :=\sum_{|\beta| = \lfloor r \rfloor} \langle D^{\beta}u \rangle^{r- \lfloor r \rfloor}. $$

Linear Cauchy problem

Consider a linear second-order differential operator

$$L u:=\frac {\partial u}{\partial t} - { \sum_{i,j=1}^{d}} a_{ij}(t,x) \frac {\partial^{2} u}{\partial x_{i} \partial x_{j}} - { \sum_{i=1}^{d}} b_{i}(t,x) \frac {\partial u}{\partial x_{i}} - c(t,x)u, $$

where the coefficients $a,b,c$ are defined on $[0,T]\times \mathbb{R}^{d}$ and $(a_{i,j}(t,x))_{i,j}$ is a symmetric matrix for all $(t,x) \in [0,T]\times \mathbb{R}^{d}$. The main existence and uniqueness result for linear Cauchy problems in $\mathbb{R}^{d}$, Theorem C.1 below, relies on the following conditions:

$(\mathrm{P1})$ :

The operator $L$ is uniformly parabolic, i.e., there exist $0< c_{1}< c_{2}<\infty$ such that for every $(t,x)\in[0,T]\times \mathbb{R}^{d}$, we have

$$c_{1} |y|^{2} \leq { \sum_{i,j=1}^{d}} a_{ij}(t,x) y_{i} y_{j} \leq c_{2} |y|^{2} \quad \text{for all }y\in \mathbb{R}^{d}. $$

$(\mathrm{P2})^{r}$ :

For all $i,j=1,\dots,d$, we have $a_{i,j}, b_{i}, c \in H^{r/2,r}([0,T]\times \mathbb{R}^{d})$.

Theorem C.1

Suppose $(\mathrm{P1})$ and $(\mathrm{P2})^{r}$ are satisfied with $r\in \mathbb{R}_{+}$, $r\notin \mathbb{N}$, and let $\varphi\in H^{r+2}(\mathbb{R}^{d})$ and $f\in H^{r/2,r}([0,T]\times \mathbb{R}^{d})$. Then there exists a unique function $u\in H^{(r+2)/2,r+2}([0,T]\times \mathbb{R}^{d})$ such that

$$L u = f, \quad u(0,{\,\cdot \,}) = \varphi. $$

Moreover, $u$ satisfies

$$\|u \|_{H}^{r/2 +1, r+2} \leq c \left( \|\varphi\|_{H}^{r+2} + \|f\|^{r/2, r}_{H} \right), $$

where $c>0$ is a global constant that is independent of $\varphi$ and $f$.

Proof

See [29, Theorem IV.5.1]. □

As a special case, we obtain the result we have used in the proof of Lemma 7.1.

Corollary C.2

Suppose that

(C1):

$a, b, c: \mathbb{R}\to \mathbb{R}$ are bounded and Lipschitz-continuous;

(C2):

the function $a$ has a bounded Lipschitz-continuous derivative and satisfies $\inf_{y \in \mathbb{R}} a (y) >0$;

($\mathrm{C3}^{\prime}$):

$\hat{\varepsilon}\in H^{r+2}(\mathbb{R})$ for some $r \in (0,1)$.

Then for each bounded and Lipschitz-continuous function $f: [0,T] \times \mathbb{R}\to \mathbb{R}$, there exists a unique $g\in C_{b}^{1,2}([0,T] \times \mathbb{R})$ that solves

$$ 0 = g_{t} + a g_{yy} + b g_{y} + c g + f, \quad g(T,{\,\cdot \,}) = \hat{\varepsilon}. $$

Proof

Consider the second-order differential operator

$$L u = \frac {\partial u}{\partial t} - a \frac {\partial^{2} u}{\partial y \partial y} - b \frac {\partial u}{\partial y} - c u. $$

By assumptions (C1) and (C2), the differential operator $L$ satisfies (P1) and $(\mathrm{P2})^{r}$ for $r \in (0,1)$. Moreover, $f$ is in $H^{r/2,r}([0,T] \times \mathbb{R})$ since it is Lipschitz-continuous. Hence Theorem C.1 yields $u\in H^{(r+2)/2,r+2}([0,T] \times \mathbb{R})$ such that

$$Lu = f(T-t, \cdot),\quad u(0,{\,\cdot \,}) = \hat{\varepsilon}\quad\text{and}\quad \|u\|_{C^{1,2}} \leq \|u \|_{H}^{(r+2)/2,r+2} < \infty. $$

Thus defining $g\in C_{b}^{1,2}([0,T]\times \mathbb{R})$ by $g(t,y) :=u(T-t, y)$, we obtain

$$0 = g_{t} + a g_{yy} + b g_{y} + c g + f, \quad g(T,\cdot) = \hat{\varepsilon}. $$

 □

Quasilinear Cauchy problem

Next consider the nonlinear differential operator

$$Lu:=u_{t} - { \sum_{i=1}^{d}} \left(\frac {\,\mathrm{d}}{\,\mathrm{d} x_{i}} a_{i}(t,x, u, u_{x}) \right) + a(t,x,u,u_{x}) $$

with principal part in divergence form. We set

$$\begin{aligned} \begin{aligned} a_{ij}(t,x,u,p)&:=\frac {\partial a_{i}(x,t,u,p)}{\partial p_{j}}, \\ A (t,x,u,p)&:=a(t,x,u,p) - { \sum_{i=1}^{d}} \bigg( \frac {\partial a_{i}}{\partial u} p_{i} + \frac {\partial a_{i}}{\partial x_{i}} \bigg). \end{aligned} \end{aligned}$$

(C.1)

We now state the conditions required for Theorem C.3.

• (Q1) For all $t\in(0,T]$, $x,p\in \mathbb{R}^{d}$ and $u\in \mathbb{R}$, we have

  $${ \sum_{i,j=1}^{d}} a_{ij}(t,x,u,p) y_{i} y_{j} \geq 0\quad \text{for all } y \in \mathbb{R}^{d}. $$

• (Q2) There exist $b_{1}, b_{2} \geq 0$ such that for all $t \in (0,T]$, $x \in \mathbb{R}^{d}$ and $u \in \mathbb{R}$, we have

  $$A(t,x,u,0) \geq - b_{1} u^{2} - b_{2}. $$

• (Q3) The functions $a$ and $a_{i}$ are continuous, and $a_{i}$ is differentiable with respect to $x$, $u$ and $p$. Moreover, there exist $c_{1}, c_{2} >0$ such that for all tuples $v =(t,x,u,p)$ in $[0,T]\times \mathbb{R}^{d} \times \mathbb{R}\times \mathbb{R}^{d}$, we have

  $$c_{1}|y|^{2} \leq { \sum_{i,j=1}^{n}} a_{ij}(v) y_{i} y_{j} \leq c_{2} |y|^{2}\quad \text{for all } y\in \mathbb{R}^{d} $$

  and, with $a_{ij}$ given by (C.1),

$$|a(v)| + { \sum_{i=1}^{d}} \bigg(|a_{i}(v)| + \bigg| \frac {\partial a_{i}(v)}{\partial u}\bigg| \bigg) (1+ |p|) + { \sum_{i,j=1}^{d}} |a_{ij}(v)|\\ \leq c_{2}(1+ |u|) (1 + |p|)^{2}. $$

$(\mathrm{Q4})^{\beta}$ :

There exists $\beta\in(0,1)$ such that for all compact sets $K\subset \mathbb{R}$, $\bar{K} \subset \mathbb{R}^{d}$, the functions

$$a_{i}, a, a_{ij}, \frac{\partial a_{i}}{\partial u}, \frac{\partial a_{i}}{\partial x_{i}}: [0,T] \times \mathbb{R}^{d} \times K \times \bar{K} \to \mathbb{R}$$

are Hölder-continuous in $t,x,u$ and $p$ with exponents $\beta/2$, $\beta$, $\beta$ and $\beta$, respectively.

Here we say that $f:[0,T] \times \mathbb{R}^{d} \times K \times \bar{K} \to \mathbb{R}, z= (z^{1},z^{2}, z^{3}, z^{4})\mapsto f(z)$ is $\beta$-Hölder-continuous in $z^{i}$ if

$$\langle u\rangle^{\beta}_{i}:=\sup_{z, \bar{z} \in \operatorname{dom}(f),\ z^{j} = \bar{z}^{j}, \ j \neq i ,\ |z^{i}-\bar{z}^{i}| \leq 1} \frac {|f(z) - f(\bar{z})|}{|z^{i} - \bar{z}^{i}|^{\beta}} < \infty. $$

Theorem C.3

Suppose $\psi_{0}$ is in $H^{2+\beta}(\mathbb{R}^{d})$ and (Q1), (Q2), (Q3) and (Q4)^β are satisfied for some $\beta \in (0, 1)$. Then there exists a solution $u \in H^{(2+ \beta)/2, 2+ \beta}([0,T] \times \mathbb{R}^{d})$ of the Cauchy problem

$$Lu = 0,\qquad u(0,\cdot) =\psi_{0}. $$

Proof

See [29, Theorem V.8.1]. □

In the proof of Theorem 6.10, we require the following ramification of this result.

Corollary C.4

Suppose that

(C1):

$a, b, c: \mathbb{R}\to \mathbb{R}$ are bounded and Lipschitz-continuous;

(C2):

the function $a$ has a bounded Lipschitz-continuous derivative and satisfies $\inf_{y \in \mathbb{R}} a (y) >0$;

($\mathrm{C3}^{\prime}$):

$\hat{\varepsilon}\in H^{r+2}(\mathbb{R})$ for some $r \in (0,1)$;

and let $f\in C^{1}_{b}(\mathbb{R})$. Then the semilinear PDE

$$ 0 = g_{t} + ag_{yy} +b g_{y} + cg + f(g), \qquad g(T,\cdot) = \hat{\varepsilon}$$

has a solution $g\in C_{b}^{1,2}([0,T]\times \mathbb{R})$.

Proof

After setting $a_{1}(t,x,u,p):=p a(x)$ and

$$ \bar{a}(t,x,u,p):=-b(x) p - c(x) u - f(u) + p a'(x), $$

we can represent the relevant differential operator as

$$\begin{aligned} L u :=& u_{t} - \frac {\,\mathrm{d}}{\,\mathrm{d} x} a_{1}(t,x,u, u_{x}) + \bar{a}(t,x,u, u_{x})\\ \ =& u_{t} - \frac {\,\mathrm{d}}{\,\mathrm{d} x} \big(u_{x} a(x)\big) - b(x) u_{x} -c(x) u - f(u) + u_{x} a'(x)\\ \ =& u_{t} - a(x) u_{xx} - b(x) u_{x} -c(x) u - f(u). \end{aligned}$$

Hence if $u \in C_{b}^{1,2}([0,T]\times \mathbb{R})$ solves $Lu=0$, $u(0,\cdot)=\hat{\varepsilon}$, then $g(t,x):=u(T-t,x)$ defines a member of $C_{b}^{1,2}([0,T]\times \mathbb{R})$ that satisfies

$$ 0= g_{t}+ a g_{yy} + bg_{y} +cg + f(g),\quad g(T,\cdot) = \hat{\varepsilon}. $$

We now verify the assumptions of Theorem C.3 for $L$. Note that

$$a_{11}(t,x,u,p) = \frac {\partial a_{1}(x,t,u,p)}{\partial p_{1}} =a(x), $$

so (Q1) holds since

$$a_{11}(t,x,u,p) y^{2} = a(x) y^{2} \geq 0 \quad \text{by (C2).} $$

Next observe that

$$\begin{aligned} A(t,x,u,p) &= \bar{a}(t,x,u,p) - \frac {\partial a_{1}(t,x,u,p)}{\partial u} p - \frac {\partial a_{1}(t,x,u,p)}{\partial x} \\ &= - b(x) p -c (x) u - f(u). \end{aligned}$$

Thus (Q2) is satisfied since

$$A(t,x,u,0) = -c (x) u - f(u) \geq - \|c\|_{\infty}|u| - \|f\|_{\infty}\geq - b_{1} u^{2} - b_{2} $$

with $b_{1}:=\|c\|_{\infty}$ and $b_{2}:=\|c\|_{\infty}+ \|f\|_{\infty}$. To check (Q3), note that by (C1) and (C2), the functions $a_{1}$ and $\bar{a}$ are continuous, and $a_{1}$ is differentiable; moreover,

$$\inf_{x \in \mathbb{R}} a(x) |y|^{2} \leq a_{11}(t,x,u,p) y^{2} \leq \|\beta\|_{\infty}|y|^{2} $$

for all $t \in [0,T]$ and $x,u,p,y \in \mathbb{R}$. For all $v = (t,x,u,p) \in [0,T] \times \mathbb{R}\times \mathbb{R}\times \mathbb{R}$, we further have

$$\begin{aligned} & |\bar{a}(v)| + \bigg(|a_{1}(v)| + \bigg| \frac {\partial a_{1}(v)}{\partial u}\bigg|\bigg) (1+ |p|) + |a_{11}(v)|\\ &\quad{}\leq \|b\|_{\infty}|p| + \|c\|_{\infty}|u| + \|f\|_{\infty}+ \|a'\|_{\infty}|p| + |p| \|a\|_{\infty}(1+ |p|) + \|a\|_{\infty}\\ &\quad{}\leq \big(\|a\|_{\infty}+ \|b\|_{\infty}+ \|c\|_{\infty}+ \|f\|_{\infty}+ \|a'\|_{\infty}\big) (1+ |u|) (1 + |p|)^{2}, \end{aligned}$$

since $a,b,c,f$ and $a'$ are bounded. Thus (Q3) holds with

$$c_{2}:=\|a\|_{\infty}+ \|b\|_{\infty}+ \|c\|_{\infty}+ \|f\|_{\infty}+ \|a'\|_{\infty}$$

and $c_{1}:=\inf_{x \in \mathbb{R}} a(x) >0$. Finally, for any compact set $K \subset \mathbb{R}$, the functions

$$\begin{aligned} &a_{1}(v) =p a(x), \quad a(v)=-b(x) p - c(x) u - f(u) + p a'(x),\\ &a_{11}(v)= a(x),\quad \frac{\partial a_{1}}{\partial u}(v)=0, \quad \frac{\partial a_{1}}{\partial p}(v) = a'(x) \end{aligned}$$

restricted to $[0,T] \times \mathbb{R}\times K \times K$ are Lipschitz-continuous in $x$, $u$ and $p$, because $a$, $a'$, $b$, $c$ and $f$ are bounded and Lipschitz by (C1), (C2) and since $f \in C_{b}^{1}(\mathbb{R})$. Hence (Q4)$^{\frac{1}{2}}$ holds as well. Thus by Theorem C.3, the Cauchy problem

$$L u = 0, \quad u(0,\cdot) =\hat{\varepsilon}$$

has a solution $u \in H^{5/4,5/2}([0,T] \times \mathbb{R}^{d}) \subset C_{b}^{1,2} ([0,T] \times \mathbb{R}^{d})$. Uniqueness follows from standard BSDE arguments; see e.g. [20, Proposition 4.3]. □