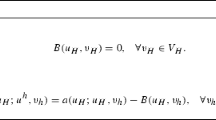Skip to main content
Springer Nature Link
Log in

Two-grid optimality for Galerkin linear systems based on B-splines

  • S.I.: EMG 2014
  • Published:
Computing and Visualization in Science

Abstract

A multigrid method for linear systems stemming from the Galerkin B-spline discretization of classical second-order elliptic problems is considered. The spectral features of the involved stiffness matrices, as the fineness parameter h tends to zero, have been deeply studied in previous works, with particular attention to the dependencies of the spectrum on the degree p of the B-splines used in the discretization process. Here, by exploiting this information in connection with \(\tau \)-matrices, we describe a multigrid strategy and we prove that the corresponding two-grid iterations have a convergence rate independent of h for \(p=1,2,3\). For larger p, the proof may be obtained through algebraic manipulations. Unfortunately, as confirmed by the numerical experiments, the dependence on p is bad and hence other techniques have to be considered for large p.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Notes

  1. Take into account that these statements hold when the discretization steps \(h_i=1/n_i\) in each direction \(x_i\) tend to 0 with the same speed. This happens, for instance, when \(n_i=\nu _in,\ \varvec{\nu }:=(\nu _1,\ldots ,\nu _d)\) is fixed and \(n\rightarrow \infty \).

  2. The first property holds because \(q_d\) is nonnegative and, by a direct computation,

    $$\begin{aligned} \sum \nolimits _{{\widehat{{\varvec{\theta }}}}\in {\mathcal {M}}({\varvec{\theta }})\cup \{{\varvec{\theta }}\}}q_d({\widehat{{\varvec{\theta }}}})=2^d>0,\quad \forall {\varvec{\theta }}\in [0,\pi ]^d. \end{aligned}$$

References

  1. Aricò, A., Donatelli, M.: A V-cycle multigrid for multilevel matrix algebras: proof of optimality. Numer. Math. 105, 511–547 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  2. Aricò, A., Donatelli, M., Serra-Capizzano, S.: V-cycle optimal convergence for certain (multilevel) structured linear systems. SIAM J. Matrix Anal. Appl. 26, 186–214 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  3. Axelsson, O., Lindskog, G.: On the rate of convergence of the preconditioned conjugate gradient method. Numer. Math. 48, 499–523 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  4. Beckermann, B., Serra-Capizzano, S.: On the asymptotic spectrum of finite element matrix sequences. SIAM J. Numer. Anal. 45, 746–769 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  5. Bhatia, R.: Matrix Analysis. Springer, New York (1997)

    Book  Google Scholar 

  6. Boor, C. de: A Practical Guide to Splines. Springer, New York (2001)

  7. Cottrell, J.A., Hughes, T.J.R., Bazilevs, Y.: Isogeometric Analysis: Toward Integration of CAD and FEA. Wiley, Chichester (2009)

  8. Donatelli, M.: An algebraic generalization of local Fourier analysis for grid transfer operators in multigrid based on Toeplitz matrices. Numer. Linear Algebra Appl. 17, 179–197 (2010)

    MathSciNet  MATH  Google Scholar 

  9. Donatelli, M., Garoni, C., Manni, C., Serra-Capizzano, S., Speleers, H.: Robust and optimal multi-iterative techniques for IgA Galerkin linear systems. Comput. Methods Appl. Mech. Eng. 284, 230–264 (2015)

    Article  MathSciNet  Google Scholar 

  10. Donatelli, M., Garoni, C., Manni, C., Serra-Capizzano, S., Speleers, H.: Robust and optimal multi-iterative techniques for IgA collocation linear systems. Comput. Methods Appl. Mech. Eng. 284, 1120–1146 (2015)

    Article  MathSciNet  Google Scholar 

  11. Donatelli, M., Garoni, C., Manni, C., Serra-Capizzano, S., Speleers, H.: Symbol-based multigrid methods for Galerkin B-spline isogeometric analysis, submitted

  12. Fiorentino, G., Serra, S.: Multigrid methods for Toeplitz matrices. Calcolo 28, 283–305 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  13. Fiorentino, G., Serra, S.: Multigrid methods for symmetric positive definite block Toeplitz matrices with nonnegative generating functions. SIAM J. Sci. Comput. 17, 1068–1081 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  14. Gahalaut, K.P.S., Kraus, J.K., Tomar, S.K.: Multigrid methods for isogeometric discretization. Comput. Methods Appl. Mech. Eng. 253, 413–425 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  15. Garoni, C.: Structured matrices coming from PDE approximation theory: spectral analysis, spectral symbol and design of fast iterative solvers. Ph.D. Thesis in Mathematics of Computation, University of Insubria, Como, Italy. http://hdl.handle.net/10277/568 (2015)

  16. Garoni, C., Manni, C., Pelosi, F., Serra-Capizzano, S., Speleers, H.: On the spectrum of stiffness matrices arising from isogeometric analysis. Numer. Math. 127, 751–799 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  17. Garoni, C., Manni, C., Serra-Capizzano, S., Sesana, D., Speleers, H.: Spectral analysis and spectral symbol of matrices in isogeometric Galerkin methods. Technical Report 2015-005, Department of Information Technology, Uppsala University, Sweden (2015)

  18. Hughes, T.J.R., Cottrell, J.A., Bazilevs, Y.: Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Methods Appl. Mech. Eng. 194, 4135–4195 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  19. Jin, X.Q.: Developments and Applications of Block Toeplitz Iterative Solvers. Kluwer Academic Publishers, Dordrecht (2002)

    Google Scholar 

  20. Ruge, J.W., Stüben, K.: Algebraic multigrid, Chapter 4 of the book Multigrid Methods by S. McCormick. SIAM Publications, Philadelphia (1987)

    Google Scholar 

  21. Serra, S.: Multi-iterative methods. Comput. Math. Appl. 26, 65–87 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  22. Serra-Capizzano, S.: Convergence analysis of two-grid methods for elliptic Toeplitz and PDEs matrix-sequences. Numer. Math. 92, 433–465 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  23. Serra-Capizzano, S.: Generalized locally Toeplitz sequences: spectral analysis and applications to discretized partial differential equations. Linear Algebra Appl. 366, 371–402 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  24. Serra-Capizzano, S.: The GLT class as a generalized Fourier analysis and applications. Linear Algebra Appl. 419, 180–233 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  25. Serra-Capizzano, S., Tablino-Possio, C.: Spectral and structural analysis of high precision finite difference matrices for elliptic operators. Linear Algebra Appl. 293, 85–131 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  26. Serra-Capizzano, S., Tablino-Possio, C.: Positive representation formulas for finite difference discretizations of (elliptic) second order PDEs. Contemp. Math. 281, 295–318 (2001)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgments

This work was partially supported by INdAM-GNCS Gruppo Nazionale per il Calcolo Scientifico, by the MIUR ‘Futuro in Ricerca 2013’ Programme through the project DREAMS, by the MIUR-PRIN 2012 N. 2012MTE38N, and by the Donation KAW 2013.0341 from the Knut & Alice Wallenberg Foundation in collaboration with the Royal Swedish Academy of Sciences, supporting Swedish research in mathematics.

Author information

Authors and Affiliations

  1. Department of Science and High Technology, University of Insubria, Via Valleggio 11, 22100, Como, Italy

    Marco Donatelli, Carlo Garoni & Stefano Serra-Capizzano

  2. Department of Mathematics, University of Rome ‘Tor Vergata’, Via della Ricerca Scientifica, 00133, Rome, Italy

    Carlo Garoni, Carla Manni & Hendrik Speleers

  3. Division of Scientific Computing, Department of Information Technology, Uppsala University, Box 337, 751 05, Uppsala, Sweden

    Stefano Serra-Capizzano

Authors
  1. Marco Donatelli
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Carlo Garoni
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Carla Manni
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Stefano Serra-Capizzano
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Hendrik Speleers
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Hendrik Speleers.

Additional information

Communicated by Artem Napov, Yvan Notay, and Stefan Vandewalle.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Donatelli, M., Garoni, C., Manni, C. et al. Two-grid optimality for Galerkin linear systems based on B-splines. Comput. Visual Sci. 17, 119–133 (2015). https://doi.org/10.1007/s00791-015-0253-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00791-015-0253-z

Keywords

Mathematics Subject Classification