Abstract
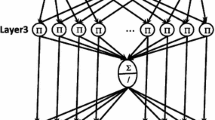
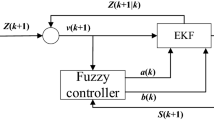
This paper presents an alternative solution to simultaneous localization and mapping (SLAM) problem by applying a fuzzy Kalman filter using pseudolinear process and measurement models. Nonlinear process model and observation model are formulated as pseudo-linear models and rewritten with a composite model whose local models are linear according to Takagi-Sugeno (T-S) fuzzy model. Using the Kalman filter theory, each local T-S model is filtered to find the local estimates. The linear combination of these local estimates gives the global estimate for the complete system. Data association to correspond features to the observed measurement is proposed with two sensor frames obtained from two sensors. The above system is implemented and simulated with Matlab to claim that the proposed method yet finds a better solution to the SLAM problem, though nonlinearity is directly involved in the Kalman filter equations, compared to the conventional approach.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Durrant-Whyte H, Bailey T (2006) Simultaneous localization and mapping: Part I. IEEE Robotics and Automaton Magazine 13(2):99–108
Smith R, Self M, Cheeseman P (1987) A stochastic map for uncertain spatial relationships. Proceedings of the 4th Int Symp Robot Res, University of California, Santa Clara, CA, pp 467–474
Leonard JJ, Durrant-White HF (1991) Mobile robot localization by tracking geometric beacons. IEEE Trans on Robotics and Automation 7(3):376–382
Dissanayake MWMG, Newman P, Clark S, et al (2001) A solution to the simultaneous localization and map building (SLAM) problem. IEEE Trans on Robotics and Automation 17(3):229–241
Li XR, Jikov VP (2001) A survey of maneuvering target tracking-part III: measurement models. In: Proceedings of the SPIE Conference on Signal and Date Processing of Small Targets, San Diego, CA, pp 423–446
Whitcombe DW (1972) Pseudo state measurements applied to recursive nonlinear filtering. In: Proceedings of the 3rd Symp Nonlinear Estimation Theory and Its Application, San Diego, CA, pp 278–281
Chen G, Xie Q, Shieh LS (1998) Fuzzy Kalman filtering. J Information Sci 109:197–209
Takagi T, Sugeno M (1985) Fuzzy identification of systems and its applications to modeling and control. IEEE Trans Syst Man Cybern 15:116–132
Smith R, Self M, Cheeseman P (1990) Estimating uncertain spatial relationships in robotics. In: Autonomous Robot Vehicles, Cox IJ, Wilfon GT (eds), Springer, New York, pp 167–193
Aidala VJ (1979) Kalman filter behavior in bearings-only tracking applications. IEEE Trans Aerospace Electronic Systems 15(1):29–39
Lindgren AG, Gong KF (1978) Position and velocity estimation via bearing observations. IEEE Trans Aerospace Electronic Systems 14(4):564–577
Tanaka K, Ikeda T, Wang H (1996) Robust stabilization of a class of uncertain nonlinear system via fuzzy control. IEEE Trans Fuzzy Syst 4:1–13
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was presented in part at the 13th International Symposium on Artificial Life and Robotics, Oita, Japan, January 31–February 2, 2008
About this article
Cite this article
Pathiranage, C.D., Watanabe, K. & Izumi, K. A fuzzy logic based approach to the SLAM problem using pseudolinear models with multiframe data association. Artif Life Robotics 13, 155–161 (2008). https://doi.org/10.1007/s10015-008-0566-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10015-008-0566-9