Skip to main content
Springer Nature Link
Log in

A fast identification algorithm with outliers under Box-Cox transformation-based annealing robust radial basis function networks

  • Original Article
  • Published:
Artificial Life and Robotics Aims and scope Submit manuscript

Abstract

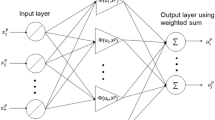
In this article, a Box-Cox transformation-based annealing robust radial basis function networks (ARRBFNs) is proposed for an identification algorithm with outliers. Firstly, a fixed Box-Cox transformation-based ARRBFN model with support vector regression (SVR) is derived to determine the initial structure. Secondly, the results of the SVR are used as the initial structure in the fixed Box-Cox transformation-based ARRBFNs for the identification algorithm with outliers. At the same time, an annealing robust learning algorithm (ARLA) is used as the learning algorithm for the fixed Box-Cox transformation-based ARRBFNs, and applied to adjust the parameters and weights. Hence, the fixed Box-Cox transformation-based ARRBFNs with an ARLA have a fast convergence speed for an identification algorithm with outliers. Finally, the proposed algorithm and its efficacy are demonstrated with an illustrative example in comparison with Box-Cox transformation-based radial basis function networks.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Hong X (2007) Modified radial basis function neural network using output transformation. IET Control Theor Appl 1:1–8

    Article  MATH  Google Scholar 

  2. Hong X, Harris CJ (2003) Experimental design and model construction algorithms for radial basis function networks. Int J Syst Sci 34(14–15):733–745

    Article  MATH  Google Scholar 

  3. Box GEP, Cox DR (1964) An analysis of transformation (with discussion). J R Stat Soc Ser B 26:211–252

    MATH  MathSciNet  Google Scholar 

  4. Hong X (2006) A fast identification algorithm for Box-Cox transformation-based radial basis function neural network. IEEE Trans Neural Networks 17:1064–1069

    Article  Google Scholar 

  5. Hong YP, Pan CT (1992) Rank-revealing QR factorizations and the singular value decomposition. Math Comput 58(192):213–232

    MATH  MathSciNet  Google Scholar 

  6. Hawkins DM (1980) Identification of outliers. Chapman & Hall, London, pp 1–30

    MATH  Google Scholar 

  7. Chuange CC, Jeng JT, Lin PT (2004) Annealing robust radial basis function networks for function approximation with outliers. Neurocomputing 56:123–139

    Article  Google Scholar 

  8. Vapnik V (1995) The nature of statistical learning theory. Springer, Berlin, pp 181–217

    MATH  Google Scholar 

  9. Vapnik V, Golowich S, Smola AJ (1997) Support vector method for function approximation, regression estimation, and signal processing. Neural Inf Process Syst 9:281–287

    Google Scholar 

  10. Chuang CC, Su SF, Hsiao CC (2000) The annealing robust backpropagation (BP) learning algorithm. IEEE Trans Neural Networks 11:1067–1077

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Graduate School of Engineering Science and Technology, National Yunlin University of Science and Technology, Douliou, Yunlin, 640, Taiwan

    Pi-Yun Chen

  2. Department of Electrical Engineering, National Yunlin University of Science and Technology, Douliou, Yunlin, 640, Taiwan

    Chia-Ju Wu

  3. Department of Automation Engineering, Nan Kai University of Technology, Tsaotun, Nantou, 542, Taiwan

    Chia-Nan Ko

  4. Department of Computer Science and Information Engineering, National Formosa University, Huwei, Yunlin, 632, Taiwan

    Jin-Tsong Jeng

Authors
  1. Pi-Yun Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Chia-Ju Wu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Chia-Nan Ko
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Jin-Tsong Jeng
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Pi-Yun Chen.

Additional information

This work was presented in part at the 14th International Symposium on Artificial Life and Robotics, Oita, Japan, February 5–7, 2009

About this article

Cite this article

Chen, PY., Wu, CJ., Ko, CN. et al. A fast identification algorithm with outliers under Box-Cox transformation-based annealing robust radial basis function networks. Artif Life Robotics 14, 62–66 (2009). https://doi.org/10.1007/s10015-009-0629-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10015-009-0629-6

Key words