Modeling and robust decoupling control for hypersonic scramjet vehicle

Abstract

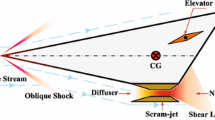
In this paper, the modeling and the robust decoupling control for a generic hypersonic scramjet vehicle are studied. Firstly, the dynamics of the hypersonic vehicle are modeled by applying the Lagrangian approach, which captures the most primary characteristics such as elastic deformation, aerodynamics, aero-heating, variable mass, effect of spherical rotating earth and their inherent interactions. Then, a robust output decoupling controller is designed by using nonlinear dynamic inversion plus the desired proportional integral dynamics, and natural time-scale separation theorem between fast and slow variables. Finally, the nonlinear simulations confirm the effectiveness of the robust decoupling controller.

Appendix

Force equations:

$$ \begin{aligned} \dot{u}&=[\omega_{z}+\omega_{E}(T_{31}c\lambda-T_{33}s\lambda)]v\\ &-[\omega_{y}+\omega_{E}(T_{21}c\lambda-T_{23}s\lambda]w +gT_{13}+(F_{x}+\Uppsi_{F_{x}})/m\\ \dot{v}&=[\omega_{x}+\omega_{E}(T_{11}c\lambda-T_{13}s\lambda)]w\\ &-[\omega_{z}+\omega_{E}(T_{31}c\lambda-T_{33}s\lambda)]u +gT_{23}+(F_{y}+\Uppsi_{F_{y}})/m\\ \dot{w}&=[\omega_{y}+\omega_{E}(T_{21}c\lambda-T_{23}s\lambda)]u\\ &-[\omega_{x}+\omega_{E}(T_{11}c\lambda-T_{13}s\lambda)]v +gT_{33}+(F_{z}+\Uppsi_{F_{z}})/m \end{aligned} $$

Moment equations:

$$ \begin{aligned} &J_{xx}\dot{\omega}_{x}-J_{xz}\dot{\omega}_{z} =J_{xz}\omega_{x}\omega_{y}+(J_{yy}-J_{zz})\omega_{y}\omega_{z} +\bar{M}_{x}+\Uppsi_{\bar{M}_{x}}\\ &J_{yy}\dot{\omega}_{y}=(J_{zz}-J_{xx})\omega_{x}\omega_{z} +J_{xz}(\omega_{z}^{2}-\omega_{x}^{2}) +\bar{M}_{y}+\Uppsi_{\bar{M}_{y}}\\ &J_{zz}\dot{\omega}_{z}-J_{xz}\dot{\omega}_{x}= -J_{xz}\omega_{y}\omega_{z}+(J_{xx}-J_{yy})\omega_{x}\omega_{y} +\bar{M}_{z}+\Uppsi_{\bar{M}_{z}} \end{aligned} $$

Euler angle equations:

$$ \begin{aligned} \dot{\phi}&=\omega_{x}+(\omega_{z}c\phi+\omega_{y}s\phi)t\theta -(c\theta{c}\phi+s\theta{c}\phi{t}\theta)(v/R)\\ &\quad+(c\theta{s}\phi+s\theta{s}\phi{t}\theta)(w/R) -\omega_{E}(c\psi{s}\theta{t}\theta+c\psi{c}\theta)c\lambda\\ \dot{\theta}&=\omega_{y}c\phi-\omega_{z}s\phi +c\theta(u/R)+s\theta{s}\phi(v/R)+s\theta{c}\phi(w/R)\\ &\quad+\omega_{E}s\psi{c}\lambda\\ \dot{\psi}&=(1/c\theta)(\omega_{z}c\phi+\omega_{y}s\phi)-\omega_{E}(c\psi{t}\theta{c}\lambda-s\lambda)\\ &\quad+s\psi{c}\theta{t}\lambda(u/R) +[(s\psi{s}\theta{s}\phi+c\psi{c}\phi)t\lambda-c\phi{t}\theta](v/R)\\ &\quad+[(s\psi{s}\theta{c}\phi-c\psi{s}\phi)t\lambda+s\phi{t}\theta](w/R) \end{aligned} $$

Trajectory equations:

$$ \begin{aligned} \dot{x}=T_{11}u+T_{21}v+T_{31}w\\ \dot{y}=T_{12}u+T_{22}v+T_{32}w\\ -\dot{h}=T_{13}u+T_{23}v+T_{33}w \end{aligned} $$

where $R=R_{E}+h, \lambda=\lambda_{0}+x/R_{E}, s=\sin, c=\cos, t=\tan,$

$$ [T_{ij}]= \left[\begin{array}{lll} c\psi c\theta& s\psi c\theta & -s\theta\\ c\psi s\theta s\phi-s\psi c\phi & s\psi s\theta s\phi+c\psi c\phi & c\theta s\phi\\ c\psi s\theta c\phi+s\psi s\phi & s\psi s\theta c\phi-c\psi s\phi & c\theta c\phi \end{array}\right],$$

and u, v, w, ω _x , ω _y , ω _z , ϕ, θ, ψ, x, y, h are the system states. Input control variables are $\Upphi_{x}, \Upphi_{y}, \Upphi_{z}, \delta_{e}, \delta_{a}, \delta_{r},$ which are included in the expressions of the force, moment and thrust.