Distributed model predictive consensus control for robotic swarm system

Abstract

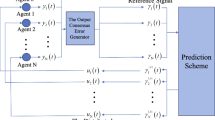
This paper proposes a distributed model predictive control method for a consensus of robotic swarm systems. The proposed method is free from any precomputed trajectories, contrast to previous studies. This is huge advantages in cases the system do not work as previously predicted, communication topology changes frequently, and the communication is unreliable. I introduce a concept of local subsystem regulator first, and then the distributed control method and its design concept are described. I also analyze stability of the proposed method and introduce how to handle constraints such as a mutual collision avoidance into the proposed method. Computer simulations are demonstrated to show effectivity of our method.

A Proof of Theorem 1

The whole system can be written as

$$\begin{aligned} x(t+1) = ( I_{N}\otimes A - \frac{1}{2}{\mathcal {L}}_{\mathrm {rw}} \otimes BK)x(t)+(I_{N}\otimes B)\varepsilon (t), \end{aligned}$$

(28)

where ${\mathcal {L}}_{\mathrm {rw}}$ denotes a random-walk normalized Laplacian matrix defined as ${\mathcal {L}}_{\mathrm {rw}}={\mathcal {D}}^{-1}{\mathcal {L}}$. Using a linear transformation $\xi = (X^{-1}\otimes I_{n_{s}})x$ and $\eta = (X^{-1}\otimes I_{n_{r}})\varepsilon$ with the matrix X diagonalizing ${\mathcal {L}}_{\mathrm {rw}}$ such that $\Lambda =X^{-1}{\mathcal {L}}_{\mathrm {rw}}X$, we get

$$\begin{aligned} \xi (t+1) = ( I_{N}\otimes A - \frac{1}{2} \Lambda \otimes BK)\xi (t)+\frac{1}{2}(I_{N}\otimes B)\eta (t), \end{aligned}$$

(29)

with $\Lambda = {\mathrm {diag}}(\lambda _{1,{\mathrm {rw}}},\ldots ,\lambda _{N,{\mathrm {rw}}})$. Here $\xi \triangleq (\xi _{1},\ldots ,\xi _{N})^{\mathrm {T}}$ indicates $\xi _{1}=\sum _{i}x_{i}/\sqrt{N}$ is average (or sum) of the agents states $x_{i}$ and the others $\xi _{i},i\ge 2$ are orthogonal to $\xi _{1}$. Therefore, if $\xi _{i},^{\forall }i\ge 2$ converge to zero, then the state x converges to the consensus manifold ${\mathcal {M}}$.

Applying the same translation to the assumption Eq. (18) as

$$\begin{aligned}&\sum _{i=1}^{N} \Vert (A-BK){\tilde{e}}_{i}(t)+B\varepsilon _{i}(t) \Vert \nonumber \\&= \Vert (I_{N}\otimes (A-BK)) {\tilde{e}}(t) + (I_{N}\otimes B) \varepsilon (t) \Vert \nonumber \\&= \Vert ({\mathcal {L}}_{\mathrm {rw}} \otimes (A-BK)) x(t) + (I_{N}\otimes B) \varepsilon (t) \Vert \nonumber \\&= \Vert (\Lambda \otimes (A-BK)) \xi (t) + (I_{N}\otimes B) \eta (t) \Vert \nonumber \\&= \sum _{i=1}^{N} \Vert \lambda _{i,{\mathrm {rw}}}(A-BK)\xi _{i}(t)+B\eta _{i}(t) \Vert \nonumber \\&\le \sum _{i=1}^{N} \beta \Vert {\tilde{e}}_{i}(t) \Vert = \beta \Vert ({\mathcal {L}}_{\mathrm {rw}} \otimes I_{n_{s}}) x(t) \Vert = \beta \Vert ( \Lambda \otimes I_{n_{s}}) \xi (t) \Vert \nonumber \\&= \sum _{i=1}^{N} \beta \Vert \lambda _{i,{\mathrm {rw}}} \xi _{i}(t) \Vert , \end{aligned}$$

(30)

we get

$$\begin{aligned} \sum _{i=2}^{N} \Vert \lambda _{i,{\mathrm {rw}}}(A-BK)\xi _{i}(t)+B\eta _{i}(t) \Vert \le \sum _{i=2}^{N} \beta \Vert \lambda _{i,{\mathrm {rw}}} \xi _{i}(t) \Vert , \end{aligned}$$

(31)

since $\lambda _{1,{\mathrm {rw}}} =0$. Then, the norm of the translated states satisfies

$$\begin{aligned}&\sum _{i=2}^{N} \Vert \xi _{i}(t+1) \Vert = \sum _{i=2}^{N} \Vert (A-\frac{\lambda _{i,{\mathrm {rw}}}}{2}BK)\xi _{i}(t)+\frac{1}{2}B\eta _{i}(t) \Vert \nonumber \\&\quad \le \sum _{i=2}^{N} \left( \Vert (1-\frac{\lambda _{i,{\mathrm {rw}}}}{2}) A\xi _{i}(t)\Vert \right. \nonumber \\&\qquad \left. + \frac{1}{2} \Vert \lambda _{i,{\mathrm {rw}}}(A-BK)\xi _{i}(t)+B\eta _{i}(t) \Vert \right) \nonumber \\&\quad \le \sum _{i=2}^{N} \left( (1-\frac{\lambda _{i,{\mathrm {rw}}}}{2}) \Vert \xi _{i}(t) \Vert + \beta \frac{\lambda _{i,{\mathrm {rw}}}}{2} \Vert \xi _{i}(t) \Vert \right) , \nonumber \\&\quad \le \sum _{i=2}^{N} \left( 1-(1-\beta )\frac{\lambda _{i,{\mathrm {rw}}}}{2}\right) \Vert \xi _{i}(t) \Vert , \end{aligned}$$

(32)

because $\lambda _{i,{\mathrm {rw}}}\in (0,2],^{\forall }i\ge 2$ (this is easily derived from eigenvalues of a symmetric normalized Laplacian ${\mathcal {L}}_{\mathrm {sym}}={\mathcal {D}}^{-1/2}{\mathcal {L}}{\mathcal {D}}^{-1/2}$, see [9]). This fact suggests the states $\xi _{i}$ orthogonal to the consensus manifold ${\mathcal {M}}$ converge to 0, thus we conclude x(t) converges to ${\mathcal {M}}$ as $t\rightarrow 0$. $\square$