Abstract
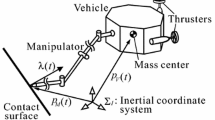
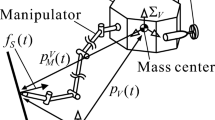
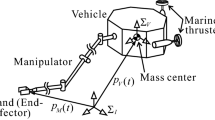
This paper deals with a motion and force control scheme for underwater robots, each of which is equipped with a manipulator. Several motion and force controllers for this type of underwater robot have been developed. Most of them were designed under the assumption that the control capability of each robot body is the same as that of each manipulator. However, it has been pointed out in the literature that for a real underwater robot, its robot body control is more challenging than its manipulator control, because the robot body has much larger inertia, and many more inaccurate position sensors and actuators than the manipulator. Therefore, even if an advanced control law with good performance is implemented in the vehicle controller of each control system, its original control performance may not be achieved. In this paper, we develop a motion and force controller for the manipulator under the condition that the robot body is independently controlled by a motion controller with poor performance. Its features are (1) to be designed in consideration of the dynamics of the robot body including its actuators (i.e., marine thrusters), (2) to ensure the stability properties in the presence of bounded disturbances, and (3) to include a linear force error filter, which can facilitate the stability analysis in comparison with existing nonlinear force error filters. Furthermore, the theoretical results were supported by those obtained in numerical simulations.







Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Sivcev S, Coleman J, Omerdic E, Dooly G, Toal D (2018) Underwater manipulators: a review. Ocean Eng 163:431–450
Antonelli G (2003) Underwater robots: motion and force control of vehicle-manipulator systems. Springer, Berlin
Antonelli G, Caccavale F, Chiaverini S, Villani L (2000) Tracking control for underwater vehicle-manipulator systems with velocity estimation. IEEE J Oceanic Eng 25(3):399–413
de Wit CC, Diaz EO, Perrier M (2000) Nonlinear control of an underwater vehicle/manipulator with composite dynamics. IEEE Trans Control Syst Technol 8(6):948–960
Sarkar N, Podder TK (2001) Coordinated motion planning and control of autonomous underwater vehicle-manipulator systems subject to drag optimization. IEEE J Oceanic Eng 26(2):228–239
Antonelli G, Caccavale F, Chiaverini S (2004) Adaptive tracking control of underwater vehicle-manipulator systems based on the virtual decomposition approach. IEEE Trans Robot Autom 20(3):594–602
Yatoh T, Sagara S, Tamura M (2008) Digital type disturbance compensation control of a floating underwater robot with 2 link manipulator. Artif Life Robot 13(1):377–381
Taira Y, Oya M, Sagara S (2010) An adaptive controller for underwater vehicle-manipulator systems including thruster dynamics. In: Proceedings of the 2010 International Conference on Modelling, Identification and Control, pp 185–190
Han J, Park J, Chung WK (2011) Robust coordinated motion control of an underwater vehicle-manipulator system with minimizing restoring moments. Ocean Eng 38(10):1197–1206
Mohan S, Kim J (2012) Indirect adaptive control of an autonomous underwater vehicle-manipulator system for underwater manipulation tasks. Ocean Eng 54:233–243
Taira Y, Oya M, Sagara S (2012) Adaptive control of underwater vehicle-manipulator systems using radial basis function networks. Artif Life Robot 17(1):123–129
Xu B, Pandian SR, Sakagami N, Petry F (2012) Neuro-fuzzy control of underwater vehicle-manipulator systems. J Franklin Inst 349(3):1125–1138
Han J, Chung WK (2014) Active use of restoring moments for motion control of an underwater vehicle-manipulator system. IEEE J Oceanic Eng 39(1):100–109
Esfahani HN, Azimirad V, Danesh M (2015) A time delay controller included terminal sliding mode and fuzzy gain tuning for underwater vehicle-manipulator systems. Ocean Eng 107:97–107
Simetti E, Casalino G (2015) Whole body control of a dual arm underwater vehicle manipulator system. Annu Rev Control 40:191–200
Taira Y, Sagara S, Oya M (2015) Robust controller with a fixed compensator for underwater vehicle-manipulator systems including thruster dynamics. Int J Adv Mechatron Syst 6(6):258–268
Mohan S, Kim J (2015) Coordinated motion control in task space of an autonomous underwater vehicle-manipulator system. Ocean Eng 104:155–167
Korkmaz O, Ider SK, Ozgoren MK (2016) Trajectory tracking control of an underactuated underwater vehicle redundant manipulator system. Asian J Control 18(5):1593–1607
Londhe PS, Mohan S, Patre BM, Waghmare LM (2017) Robust task-space control of an autonomous underwater vehicle-manipulator system by PID-like fuzzy control scheme with disturbance estimator. Ocean Eng 139:1–13
Wang Y, Jiang S, Chen B, Wu H (2017) Trajectory tracking control of underwater vehicle-manipulator system using discrete time delay estimation. IEEE Access 5:7435–7443
Dai Y, Yu S (2018) Design of an indirect adaptive controller for the trajectory tracking of UVMS. Ocean Eng 151:234–245
Haugalokken BOA, Jorgensen EK, Schjolberg I (2018) Experimental validation of end-effector stabilization for underwater vehicle-manipulator systems in subsea operations. Robot Auton Syst 109:1–12
Dai Y, Yu S, Yan Y, Yu X (2019) An EKF-based fast tube MPC scheme for moving target tracking of a redundant underwater vehicle-manipulator system. IEEE/ASME Trans Mechtron 24(6):2803–2814
Heshmati-alamdari S, Karras GC, Kyriakopoulos KJ (2019) A distributed predictive control approach for cooperative manipulation of multiple underwater vehicle manipulator systems. In: Proceedings of the International Conference on Robotics and Automation, pp 4626–4632
Han H, Wei Y, Ye X, Liu W (2020) Modeling and fuzzy decoupling control of an underwater vehicle-manipulator system. IEEE Access 8:18962–18983
Cui Y, Podder TK, Sarkar N (1999) Impedance control of underwater vehicle-manipulator systems (UVMS). In: Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, pp 148–153
Antonelli G, Chiaverini S, Sarkar N (2001) External force control for underwater vehicle-manipulator systems. IEEE Trans Robot Autom 17(6):931–938
Cui Y, Yuh J (2003) A unified adaptive force control of underwater vehicle-manipulator systems (UVMS). In: Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, pp 553–558
Olguin-Diaz E, Arechavaleta G, Jarquin G, Parra-Vega V (2013) A passivity-based model-free force-motion control of underwater vehicle-manipulator systems. IEEE Trans Rob 29(6):1469–1484
Farivarnejad H, Moosavian SAA (2014) Multiple impedance control for object manipulation by a dual arm underwater vehicle-manipulator system. Ocean Eng 89:82–98
Heshmati-Alamdari S, Bechlioulis CP, Karras GC, Nikou A, Dimarogonas DV, Kyriakopoulos KJ (2018) A robust interaction control approach for underwater vehicle manipulator systems. Annu Rev Control 46:315–325
Taira Y, Sagara S, Oya M (2018) Motion and force control with a nonlinear force error filter for underwater vehicle-manipulator systems. Artif Life Robot 23(1):103–117
Dai P, Lu W, Le K, Liu D (2020) Sliding mode impedance control for contact intervention of an I-AUV: simulation and experimental validation. Ocean Eng 196: Article No. 106855 (pp 1–11)
Choi HS (1996) Modeling of robot manipulators working under the sea and the design of a robust controller. Robotica 14(2):213–218
Lee M, Choi HS (2000) A robust neural controller for underwater robot manipulators. IEEE Trans Neural Netw 11(6):1465–1470
Yuh J, Zhao S, Lee PM (2001) Application of adaptive disturbance observer control to an underwater manipulator. In: Proceedings of the IEEE International Conference on Robotics and Automation, pp 3244–3249
Kim J, Chung WK, Yuh J (2003) Dynamic analysis and two-time scale control for underwater vehicle-manipulator systems. In: Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, pp 577–582
Taira Y, Sagara S, Oya M (2020) Model-based motion control for underwater vehicle-manipulator systems with one of the three types of servo subsystems. Artif Life Robot 25(1):133–148
Barbalata C, Dunnigan MW, Petillot Y (2018) Position/force operational space control for underwater manipulation. Robot Auton Syst 100:150–159
Yoerger DR, Cooke JG, Slotine JJE (1990) The influence of thruster dynamics on underwater vehicle behavior and their incorporation into control system design. IEEE J Oceanic Eng 15(3):167–178
Taira Y, Sagara S, Oya M (2020) Design of a motion and force controller for an underwater vehicle-manipulator system with a differently-controlled vehicle. In: Proceedings of the 25th International Symposium on Artificial Life and Robotics, pp 1025–1030
Taira Y, Sagara S, Oya M (2021) Design of an impedance controller for an underwater vehicle-manipulator system with a differently-controlled vehicle. In: Proceedings of the 26th International Symposium on Artificial Life and Robotics, pp 624–629
Craig JJ (2005) Introduction to robotics: mechanics and control, 3rd edn. Pearson Prentice Hall, New Jersey
Arimoto S (1996) Control theory of nonlinear mechanical systems: a passivity-based and circuit-theoretic approach. Oxford University Press, New York
Yuan J (1997) Adaptive control of a constrained robot-ensuring zero tracking and zero force errors. IEEE Trans Autom Control 42(12):1709–1714
Khalil HK (2002) Nonlinear system, 3rd edn. Prentice Hall, New Jersey, pp 474–475
de Queiroz MS, Dawson DM, Nagarkatti SP, Zhang F (2000) Lyapunov-based control of mechanical systems. Springer Science+Business Media, New York
Krstic M, Kanellakopoulos I, Kokotovic P (1995) Nonlinear and adaptive control design. Wiley, New York
Ioanou PA, Sun J (1996) Robust adaptive control. Prentice Hall, New Jersey
Acknowledgements
This work was supported by JSPS KAKENHI Grant Number JP21K04503.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was presented in part at the 26th International Symposium on Artificial Life and Robotics (Online, January 21–23, 2021).
Appendices
Appendix 1: Derivation of (24)
Differentiating (3) with respect to time, and then using (5), we have
Applying the relation \(R(\phi _{V})R(\phi _{V})^{\mathrm {T}} =I_{3}\) to (70), then multiplying both its sides by \(1/\Vert n_{C}(t)\Vert\), and then using the fourth equation of (21), we obtain
It should be noted that \(n_{C}(t)\) is a nonzero vector. Substituting the equation
into (71), then using the relations \(R(\phi _{V})^{\mathrm {T}} R(\phi _{V})=I_{3}\) and \(R(\phi _{V})S(\bar{a})\bar{b}=S(R(\phi _{V})\bar{a})R(\phi _{V})\bar{b}\) for any vectors \(\bar{a},\;\bar{b}\in R^{3}\), and then utilizing the first equation of (25), we can derive (24). It should be noted that (72) is an original form of (11).
Appendix 2: Derivation of third inequality of (26)
Differentiating the fourth equation of (21) with respect to time, and then using the sixth and seventh inequalities of (22), we can write the norm of \(\dot{a}_{CM}(t)\) as
where \(c_{C1}=\max \{ 1/ \Vert n_{C}(t)\Vert \}\). It should be noted that \(c_{C1}\) is a bounded positive constant, because \(n_{C}(t)\) is a nonzero vector. Utilizing (4) and (5), we obtain the inequality \(\Vert \dot{n}_{C}(t)\Vert \le c_{C2}\Vert \dot{p}_{M}(t)\Vert\), where \(c_{C2}\) is a positive constant. Applying this inequality to (73), then substituting (11) into it, and then using the first, second and sixth inequalities of (22), and the inequalities \(\Vert \dot{x}_{V}(t)\Vert \le \Vert \dot{u}(t)\Vert\) and \(\Vert \dot{q}(t)\Vert \le \Vert \dot{u}(t)\Vert\), we can derive the third inequality of (26).
Appendix 3: Derivations of (30) and (32)
For simplicity, we use the expression \(e^{\bar{x}}\) instead of the expression \(\exp (\bar{x})\) for any scalar \(\bar{x}\) in this appendix. In the derivation of (30), we utilize the inequalities
where \(\bar{c} _{1}\) to \(\bar{c}_{16}\) are positive constants.
Using the third equation of (17), we can write the norm of the solution of \(z_{VF}(t)\) as
where \(\bar{z}_{VF}(\bar{\tau })\in R^{6}\) is given by
Using the first inequality of (26), the first to eighth inequalities of (74), and the inequalities \(\Vert \dot{x}_{V}(t)\Vert \le \Vert \dot{u}(t)\Vert\) and \(\Vert \dot{q}(t)\Vert\) \(\le \Vert \dot{u}(t)\Vert\), we can rewrite (75) as
where \(\bar{c}_{VF1}\in R^{+}\) is given by
Comparing the solution of the first-order filter (31) with (76), we have
Using the first equation of (16), we can write the norm of \(z_{C}(t)\) as
Using the first inequality of (26), the first, third and fifth inequalities of (74), and the inequalities \(\Vert \dot{x}_{V}(t)\Vert \le \Vert \dot{u}(t)\Vert\) and \(\Vert \dot{q}(t)\Vert \le \Vert \dot{u}(t)\Vert\), we can rewrite (78) as
Utilizing the second equation of (19), we can write the norm of the solution of \(z_{Q}(t)\) as
Using the third, eleventh and twelfth inequalities of (74), we can rewrite (80) as
Utilizing the second equation of (21), we can write the norm of \(z_{P}(t)\) as
Utilizing (23), the first equation of (19), the third inequality of (22), the third, ninth and eleventh inequalities of (74), and the inequality \(\Vert \dot{q}(t)\Vert \le \Vert \dot{u}(t)\Vert\), we can rewrite (82) as
Applying (77), (79) and (81), to (83), we can derive (30).
In view of the condition that the disturbances \(d_{V}(t)\) and \(d_{M}(t)\) are bounded, we obtain the inequalities
where \(c_{D1}\) and \(c_{D2}\) are positive constants. Using the first equation of (17), we can write the norm of the solution of \(w_{VF1}(t)\) as
Similarly, utilizing the second equation of (17), and then applying the first inequality of (84) to it, we can write the norm of the solution of \(w_{VF2}(t)\) as
Using the third equation of (21), we can write the norm of \(w_{P}(t)\) as
Substituting the third equation of (19) and the second equation of (16) into (87), and then using (23), (85), (86), the third and eleventh inequality of (74), and the first and second inequalities of (84), we can derive (32).
Appendix 4: Derivation of (48)
The motion error \(e_{P}(t)\) with respect to \(\varSigma _{I}\) is parallel to the tangent plane \(g_{C}(p_{M})=0\), because the positions \(p_{M}(t)\) and \(p_{MRC}(t)\) are points on the plane. Therefore, the following relation holds:
Applying the relation \(R(\phi _{V})R(\phi _{V})^{\mathrm {T}}=I_{3}\) to (88), then multiplying both its sides by \(1/\Vert n_{C}(t)\Vert\), and then using the fourth equation of (21), we obtain
Using (47), and then multiplying both its sides by \(\alpha _{M}\), we have
Subtracting each side of (42) from the corresponding side of (24), and then utilizing the second equation of (45), we obtain
Finally, adding (90) to (91), and then using the first equation of (45), we can derive (48).
Appendix 5: Derivation of (54)
Using (53), and then applying the first and second inequalities of (28) to it, we can write the norm of \(f_{P1}(t)\) as
Applying the inequality \(\Vert S(\bar{x})\Vert \le 6\Vert \bar{x}\Vert\) [\(\bar{x}\in R^{3}\)] (derived from the skew-symmetric property) to (92), and then using the second and fourth inequalities of (27), we obtain
Using (52), and then applying the second inequality of (22), the second equation of (26), and the first inequality of (34) to it, we can write the norm of \(\tau _{M}(t)\) as
Applying (93) to (94), and then defining the positive constants \(\bar{c}_{T1}\) to \(\bar{c}_{T3}\) as
we can derive (54).
Appendix 6: Derivation of (55)
Differentiating (44) with respect to time, then multiplying both its sides by \(M_{P}(\phi )\), and then using the first and second equations of (45), we have
Substituting (20) into (96), and then using (53) and (57), we obtain
Substituting (52) into (97), and then using (50), we can derive (55).
Appendix 7: Proof of Theorem 1
We choose the positive definite function
Differentiating (98) with respect to time, and then substituting the error models (49), (56) and (58) into it, we have
Substituting (44) into (99), then applying (48) and the skew-symmetric property \(e_{P}^{V}(t)^{\mathrm {T}}S(\omega _{V}^{V})e_{P}^{V}(t)=0\) to it, and then defining \(W(t)\in R\) as
we obtain
It follows from (98) and (101) that the signals \(V_{1}(t)\), \(e_{H}(t)\), \(e_{P}^{V}(t)\) and \(e_{F}(t)\) are bounded. Using their bounded properties, the inequalities in the properties P1 to P6 and P9, and the assumptions A2, A3 and A9, we can prove that the other closed-loop signals are bounded.
The signals \(e_{H}(t)\), \(e_{P}^{V}(t)\) and \(e_{F}(t)\) are uniformly continuous, because their time derivatives \(\dot{e}_{H}(t)\), \(\dot{e}_{P}^{V}(t)\) and \(\dot{e}_{F}(t)\) are bounded. This means that the signal W(t) is uniformly continuous. It follows from (98), (101) and the uniform continuity of W(t) that \(\lim _{t\rightarrow \infty }W(t)=0\) (e.g., Lemma A.6 of [47]). It should be noted that instead of Lemma A.6 of [47], we can use LaSalle-Yoshizawa Theorem A.8 of [48]. In this case, instead of the uniform continuity of W(t) , it is required that the error models (49), (56) and (58) are locally Lipschitz. It follows from the zero convergence of W(t) that the error signals \(e_{P}^{V}(t)\), \(e_{H}(t)\) and \(e_{F}(t)\) are asymptotical stable. Furthermore, using (47) and the sixth inequality of (22), and then applying the asymptotic stability of \(e_{P}^{V}(t)\), we can prove that \(e_{P}(t)\) is asymptotical stable.
Integrating \(\dot{e}_{F}(t)\) from 0 to t with respect to time, and then taking its limit, we have
In the derivation of (102), we use the asymptotic stability of \(e_{F}(t)\). The Eq. (102) means that the limit of the integration of \(\dot{e}_{F}(t)\) exists and is finite. Furthermore, the boundedness of \(\ddot{e}_{F}(t)\) implies that \(\dot{e}_{F}(t)\) is uniformly continuous. Therefore, the conditions of Barbalat Lemma (e.g., Lemma A.6 of [48]) are satisfied, and hence \(\dot{e}_{F}(t)\) is asymptotically stable. Solving (49) for the term \(a_{CM}(t)e_{\varLambda }(t)\), and then applying the asymptotic stabilities of \(e_{P}^{V}(t)\), \(e_{F}(t)\) and \(\dot{e}_{F}(t)\) to it, we obtain
Moreover, it follows from (103) and the second equation of (26) that \(e_{\varLambda }(t)\) is asymptotically stable. The proof is complete.
Appendix 8: Proof of Theorem 2
We choose the positive definite function
Differentiating (104) with respect to time, and then substituting the error models (49), (55) and (56) into it, we have
where \(\dot{V}_{1}(t)\) is given by (99). Moreover, substituting (44) into (106), then applying (48) and the skew-symmetric property \(e_{P}^{V}(t)^{\mathrm {T}}S(\omega _{V}^{V})e_{P}^{V}(t)=0\) to it, and then defining \(Y_{1}(t)\in R\) as
we obtain
We can rewrite (107) as
where \(\bar{c}_{17}\) is a positive constant. In the derivation of (109), we use (32), (57), the first inequality of (28), the sixth inequality of (41), and the inequality \(\bar{a}\bar{b}\le \bar{c}\bar{a}^{2}+\bar{b}^{2}/(4\bar{c})\) [\(\bar{a},\,\bar{b}\in R\); \(\bar{c}\in R^{+}\)]. Applying (29) and (109) to (108), then defining \(\bar{c}_{18}\) and \(\alpha\) as
respectively, and then using (104), we have
Moreover, applying Lemma 3.2.4 of [49] to (110), we obtain
In a way similar to the proof of Theorem 1, except that the “bounded” disturbance term \(f_{P2}(t)\) exists, we can prove that the closed-loop signals are bounded.
In a way similar to the aforementioned analysis of \(\dot{V}_{2}(t)\), we can obtain the time derivative
where \(\bar{c}_{19}=\min \{ 1/c_{M5},\,1\}\), and \(Y_{2}(t)\in R\) is given by
In a way similar to the derivation of (109), we can rewrite (113) as
Applying (109) and (114) to (112), and then applying Lemma 3.2.4 of [49] to it, we have
We can derive (59) and (61) from (115), and furthermore, using (47), (59), and the sixth inequality of (22), we obtain (60). Similarly, we can derive the time derivative
We can derive (62) from (116), and furthermore, using (49) and the second equation of (26), we obtain (63). The proof is complete.
About this article
Cite this article
Taira, Y., Sagara, S. & Oya, M. Motion and force control with a linear force error filter for the manipulator of an underwater vehicle-manipulator system. Artif Life Robotics 27, 90–106 (2022). https://doi.org/10.1007/s10015-021-00708-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10015-021-00708-9