Beyond hybrid generative discriminative learning: spherical data classification

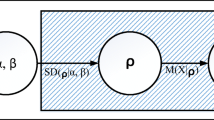
Abstract

The blending of generative and discriminative approaches has been prevailed by exploring and adopting distinct characteristic of each approach toward constructing a complementar system combining the best of both. The majority of current research in classification and categorization does not completely address the true structure and nature of data for particular application at hand. In contrast to most previous research, our proposed work focuses on the modeling and classification of spherical data that are naturally generated in many data mining and knowledge discovery applications such as text classification, visual scenes categorization and gene expression analysis. This paper investigates a generative mixture model to cluster spherical data based on Langevin distribution. In particular, we formulate a unified probabilistic framework, where we build probabilistic kernels based on Fisher score and information divergences from mixture of Langevin distributions for Support Vector Machine. We demonstrate the effectiveness and the merits of the proposed learning framework through synthetic data and challenging applications involving spam filtering using both textual and visual email contents.

Appendices

Appendix 1: Proof of Eq. 30

In the case of Langevin model, we can show that

$$ \begin{aligned} &\int\limits_{\Upomega} p({\bf X}|\Uptheta)^{\rho} q({\bf X}|\acute{\Uptheta})^{\rho} \,{\rm d}{\bf X} \\ &\quad= \left[ \left( \frac{\kappa}{2} \right)^{\frac{p}{2}-1} \frac{1}{(2 \pi)^{\frac{p}{2}} I_{\frac{p}{2}-1}(\kappa)} \right]^{\rho} \left[ \left( \frac{\acute{\kappa}}{2} \right)^{\frac{p}{2}-1} \frac{1}{(2 \pi)^{\frac{p}{2}} I_{\frac{p}{2}-1}(\acute{\kappa})} \right]^{\rho}\int\limits_{\Upomega} \left( e^{\kappa {\varvec{\mu}}^{T}{\bf X}}\right)^{\rho} \left( e^{\acute{\kappa} \acute{{\varvec{\mu}}}^{T}{\bf X}}\right)^{\rho} \,{\rm d}{\bf X} \\ &\quad= \left[ \left( \frac{\kappa}{2} \right)^{\frac{p}{2}-1} \frac{1}{(2 \pi)^{\frac{p}{2}} I_{\frac{p}{2}-1}(\kappa)} \right]^{\rho} \left[ \left( \frac{\acute{\kappa}}{2} \right)^{\frac{p}{2}-1} \frac{1}{(2 \pi)^{\frac{p}{2}} I_{\frac{p}{2}-1}(\acute{\kappa})} \right]^{\rho}\int\limits _{\Upomega} e^{(\kappa {\varvec{\mu}}+ \acute{\kappa} {\acute{\varvec{\mu}}})^{T}{\bf X} \rho } \,{\rm d}{\bf X} \end{aligned} $$

(47)

The product of two Langevin can be written as

$$ M_{p}({\bf X}| {\varvec{\mu}},\kappa)M_{p}({\bf X}| {\acute{\varvec{\mu}}},{\acute{\kappa}})\propto M_{p}({\bf X}| \tau_{{\varvec{\mu}}, {\acute{\varvec{\mu}}}},\xi_{\kappa, \acute{\kappa}}) $$

where

$$ \begin{aligned} \xi_{\kappa, \acute{\kappa}}&= \sqrt{ \kappa^2+\acute{\kappa}^2+2\kappa\acute{\kappa}({\varvec{\mu}}\acute{{\varvec{\mu}}})}\\ \tau_{{{\varvec{\mu}}}, \acute{{\varvec{\mu}}}} &= \frac{\kappa{{\varvec{\mu}}}+\acute{\kappa}\acute{{\varvec{\mu}}}}{\xi_{\kappa, \acute{\kappa}}} \end{aligned} $$

(48)

Using 48 and Langevin integral, we obtain

$$ \int\limits_{\Upomega} p({\bf X}|\Uptheta)^{\rho} q({\bf X}|\acute{\Uptheta})^{\rho} \,{\rm d}{\bf X}= \left[ \left( \frac{\kappa \acute{\kappa}}{4} \right)^{\frac{p}{2}-1} \frac{1}{(2 \pi)^{p} I_{\frac{p}{2}-1}(\kappa)I_{\frac{p}{2}-1}(\acute{\kappa})} \right]^{\rho} \left[ \frac{(2 \pi)^{\frac{p}{2}} I_{\frac{p}{2}-1}(\xi_{\kappa, \acute{\kappa}} \rho)}{(\xi_{\kappa, \acute{\kappa}} \rho)^{\frac{p}{2}-1}} \right] $$

(49)

Appendix 2: Proof of Eq. 36

The KL divergence between two exponential distributions is presented by [68]

$$ KL(p({\bf X}|\Uptheta), q({\bf X}|\acute{\Uptheta}))= \Upphi(\theta) - \Upphi(\acute{\theta}) + [G(\theta) - G(\acute{\theta})]^T E_{\theta}[T({\bf X})] $$

(50)

where E _θ is the expectation with respect to $p({\bf X}|\Uptheta), G(\theta)=(G_{1}(\theta), \ldots, G_{l}(\theta)),T({\bf X})= (T_{1}({\bf X}), \ldots, T_{l}({\bf X}))$ where l is the number of parameters of the distribution and T denotes transpose. Furthermore, we have the following:

$$ E_{\theta}[T({\bf X})]= - \acute{\Upphi}(\theta) $$

(51)

Then by letting $\Upphi_{\theta}= - a_{p}(\kappa)$ and $G_{\theta}= \kappa{\varvec{\mu}}.$ Thus, the KL divergence between two Langevin distributions is given as

$$ KL(p({\bf X}|\Uptheta), q({\bf X}|\acute{\Uptheta}))= - \log \frac{\kappa^{\frac{p}{2}-1}}{(2 \pi)^{\frac{p}{2}}I_{\frac{p}{2}-1}(\kappa)}+ \log \frac{\acute{\kappa}^{\frac{p}{2}-1}}{(2 \pi)^{\frac{p}{2}}I_{\frac{p}{2}-1}(\acute{\kappa})}+ [\kappa{\varvec{\mu}} - \acute{\kappa}{\acute{\varvec{\mu}}} ]^T \acute{a}_{p}(\kappa){\varvec{\mu}} $$

(52)

Appendix 3: Proof of Eq. 42

In the case of Langevin model, we can show the Shannon entropy is given by

$$ \begin{aligned} H[p({\bf X}|\theta)]&= - \int\limits_{\Upomega} p({\bf X}|\theta) \log p({\bf X}|\theta) \,{\rm d}{\bf X}\\ &= - \int\limits_{\Upomega} p({\bf X}|\theta) \left[ \sum_{p=1}^{P} \kappa {\varvec{\mu}}^{T} X-a_{p}(\kappa)\right] \,{\rm d}{\bf X}\\ &= - \left[ E_{\theta}[\sum_{p=1}^{P} \kappa {\varvec{\mu}}^{T} {\bf X}]- a_{p}(\kappa)\right]\\ &= \kappa a'_{p}(\kappa) {\varvec{\mu}}^{T}{\varvec{\mu}} - a_{p}(\kappa) \end{aligned} $$

(53)

Substitute Eq. 53 into Eq. 41 we obtain the Jensen–Shannon divergence for Langevin model.

Appendix 4: Proof of Eq. 44

We can show that the Rényi divergence between two Langevin distribution is given by

$$ \begin{aligned} &\int\limits_{\Upomega} p({\bf X}|\Uptheta)^{\sigma} q({\bf X}|\acute{\Uptheta})^{1-\sigma} \,{\rm d}{\bf X}\\ &\quad= \left[ \left( \frac{\kappa}{2} \right)^{\frac{p}{2}-1} \frac{1}{(2 \pi)^{\frac{p}{2}} I_{\frac{p}{2}-1}(\kappa)} \right]^{\sigma} \left[ \left( \frac{\acute{\kappa}}{2} \right)^{\frac{p}{2}-1} \frac{1}{(2 \pi)^{\frac{p}{2}} I_{\frac{p}{2}-1}(\acute{\kappa})} \right]^{1-\sigma}\int\limits _{\Upomega} \left( e^{\kappa {\varvec{\mu}}^{T}{\bf X}}\right)^{\sigma} \left( e^{\acute{\kappa} {\acute{\varvec{\mu}}}^{T}{\bf X}}\right)^{1-\sigma} \,{\rm d}{\bf X}\\ &\quad= \left[ \left( \frac{\kappa}{2} \right)^{\frac{p}{2}-1} \frac{1}{(2 \pi)^{\frac{p}{2}} I_{\frac{p}{2}-1}(\kappa)} \right]^{\sigma} \left[ \left( \frac{\acute{\kappa}}{2} \right)^{\frac{p}{2}-1} \frac{1}{(2 \pi)^{\frac{p}{2}} I_{\frac{p}{2}-1}(\acute{\kappa})} \right]^{1-\sigma}\int\limits _{\Upomega} e^{(\kappa {\varvec{\mu}}^{T}{\bf X} \sigma + \acute{\kappa}{\acute{\varvec{\mu}}}^{T}{\bf X}(1-\sigma))}\,{\rm d}{\bf X} \end{aligned} $$

(54)

Assume that $\zeta_{\kappa,\acute{\kappa}}= \sqrt{(\sigma\kappa)^2+((1-\sigma)\acute{\kappa})^2+2\sigma\kappa(1-\sigma)\acute{\kappa}({\varvec{\mu}}\cdot {\acute{\varvec{\mu}}})}$ and $\psi_{{\varvec{\mu}},\acute{\varvec{\mu}}}= \frac{\sigma\kappa{\varvec{\mu}}+(1-\sigma)\acute{\kappa}{\acute{\varvec{\mu}}}}{\zeta_{\kappa,\acute{\kappa}}},$ and hence

$$ \int\limits_{\Upomega} p({\bf X})^{\sigma} q({\bf X})^{1-\sigma} \,{\rm d}{\bf X}= \left[ \left( \frac{\kappa}{2} \right)^{\frac{p}{2}-1} \frac{1}{(2 \pi)^{\frac{p}{2}} I_{\frac{p}{2}-1}(\kappa)} \right]^{\sigma}\left[ \left( \frac{\acute{\kappa}}{2} \right)^{\frac{p}{2}-1} \frac{1}{(2 \pi)^{\frac{p}{2}} I_{\frac{p}{2}-1}(\acute{\kappa})} \right]^{1-\sigma} \left[ \frac{(2 \pi)^{\frac{p}{2}} I_{\frac{p}{2}-1}(\zeta_{\kappa,\acute{\kappa}})}{(\zeta_{\kappa,\acute{\kappa}})^{\frac{p}{2}-1}} \right] $$

(55)

By substituting Eq. 55 in Eq. 43 we obtain the symmetric Rényi divergence for two Langevin distributions.