Abstract
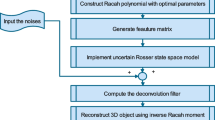
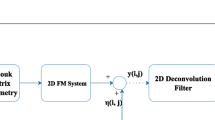
This study proposes a new approach of \(H_{\infty }\) deconvolution filtering of 2D system described by Fornasini–Marchesini model and Tchebichef moments. The challenge of this method is to generate an unknown 2D signal by transmission channel. This canal is mobilized by convolution system and deconvolution filter to rebuild the output signal. To resolve this problem, firstly, we use the Tchebichef moments to extract the feature vectors of a medicinal Cannabis sativa plant for generating the input system with the minimum information. Next, we implement the system with the model of Fornasini–Marchesini for convolution and deconvolution. However, the free matrix variables are used to eliminate coupling between Lyapunov matrix and system matrices to obtain sufficient conditions in linear matrix inequality form to ensure the desired stability and performance of the error systems. Experimental results show that the new approach for \(H_{\infty }\) deconvolution filtering of 2D systems described by the Fornasini–Marchesini model and Tchebichef moments achieves good performance than the recent works.





Similar content being viewed by others
References
Xiao B, Ma JF, Cui JT (2012) Radial Tchebichef moment invariants for image recognition. J Vis Commun Image Represent 23(2):381–386. https://doi.org/10.1016/j.jvcir.2011.11.008
Boukili B, El Mallahi M, El-Amrani A, Hmamed A, Boumhidi I (2021) \(H_{\infty }\) deconvolution filter for two-dimensional numerical systems using orthogonal moments. Optim Control Appl Methods. https://doi.org/10.1002/oca.2730
Bouagada D, Dooren PV (2011) On the stability of 2D state-space models. Numer Linear Algebra Appl. https://doi.org/10.1002/nla.836
El-Amrani A, Boukili B, Hmamed A, Boumhidi I, El Hajjaji A (2018) Robust \(H_{\infty }\) filtering for 2D continuous systems with finite frequency specifications. Int J Syst Sci. https://doi.org/10.1080/00207721.2017.1391960
El Mallahi M, Boukili B, Zouhri A, Hmamed A, Qjidaa H (2021) Robust \(H_{\infty }\) deconvolution filtering of 2-D digital systems of orthogonal local descriptor. Multim Tools Appl. https://doi.org/10.1002/oca.2730
Boukili B, Hmamed A, Benzaouia A, El Hajjaji A (2014) \(H_{\infty }\) filtering of two-dimensional T-S fuzzy systems. Circuits Syst Signal Process. https://doi.org/10.1007/s00034-013-9720-2
Chen SF, Fong IK (2006) Robust \(H_{\infty }\) filtering for 2D state-delayed systems with NFT uncertainties. IEEE Trans Signal Process 54(1):274–285
Cui JR, Hu GD (2010) State estimation of 2D stochastic systems represented by FM-II model. Acta Autom Sinica 36(5):755–761. https://doi.org/10.1016/S1874-1029(09)60034-3
Ding DW, Du X, Li X (2015) Finite-frequency model reduction of two-dimensional digital filters. IEEE Trans Autom Control 60(6):1624–1629
Du C, Xie L, Soh YC (2000) \(H_{\infty }\) filtering of 2D discrete systems. IEEE Trans Signal Process 48(6):1760–1768
Boukili B, Hmamed A, Tadeo F (2016) Robust \(H_{\infty }\) Filtering for 2D discrete Roesser systems. J Control Autom Electr Syst. https://doi.org/10.1007/s40313-016-0251-5
Li X, Gao H (2012) Robust finite frequency \(H_{\infty }\) filtering for uncertain 2D Roesser systems. Automatica 48:1163–1170
Palhares RM, Souza CED, Peres PLD (2001) Robust \(H_{\infty }\) filtering for uncertain discrete-time state-delayed systems. IEEE Trans Signal Process 49:1696–1703
Xiao B, Zhang YH, Li LP, Li WS, Wang G (2016) Explicit Krawtchouk moment invariants for invariant image recognition. J Electron Imaging. https://doi.org/10.1117/1.JEI.25.2
El Mallahi M, Mesbah A, Qjidaa H (2018) 3D radial invariant of dual Hahn moments. Neural Comput Appl 30(7):2283–2294
El Mallahi M, Zouhri A, Mesbah A, El Affar I, Qjidaa H (2018) Radial invariant of 2D and 3D Racah moments. Multim Tools Appl Int J 77(6):6583–6604
El Mallahi M, Zouhri A, EL-mekkaoui J, Qjidaa H (2017) Three dimensional radial krawtchouk moment invariants for volumetric image recognition. Pattern Recognit Image Anal 27(4):810–824
El Mallahi M et al (2017) Three dimensional radial Tchebichef moment invariants for volumetric image recognition. Pattern Recogn Image Anal 27(4):810–824
Mukundan R, Ong SH, Lee PA (2001) Discrete versus continuous orthogonal moments for image analysis. In: Internaternational conference on imaging science, systems and technology-CISST01, Las Vegas, pp 23–29
Fornasini E, Marchesini G (1976) State-space realization theory of two-dimensional filters. IEEE Trans Autom Control 21(4):484–492
Fornasini E, Marchesini G (1992) Finite memory realization of 2D FIR filters. In: IEEE international symposium on circuits and systems vol 3, pp 1444–1447
Gao H, Meng X, Chen T (2008) New design to Robust \(H_{\infty }\) filters for 2D systems. IEEE Signal Process Lett 15:217–220
Gao H, Lam J, Wang C, Xu S (2005) \(H_{\infty }\) model reduction for uncertain two-dimensional discrete systems. Optim Control Appl Meth 26:199–227
Chen SF, Fong IK (2006) Robust filtering for 2D state-delayed systems with NFT uncertainties. IEEE Trans Signal Process 54:274–285
Kririm S, Hmamed A, Tadeo F (2015) Robust \(H_{\infty }\) filtering for uncertain 2D singular Roesser models. Circuits Syst Signal Process 34(7):2213–2235. https://doi.org/10.1007/s00034-015-9967-x
Boukili B, Hmamed A, Tadeo F (2016) Reduced-order \(H_{\infty }\) filtering with intermittent measurements for a class of 2D systems. J Control Autom Electr Syst. https://doi.org/10.1007/s40313-016-0271-1
Mukundan R, Ong SH, Lee PA (2001) Image analysis by Tchebichef moments. IEEE Trans Image Process 10(9):1357–1364
Mukundan R (2004) Some computational aspects of discrete orthonormal moments. IEEE Trans Image Process 13(8):1055–1059
El Mallahi M, Zouhri A, Qjidaa H (2018) Radial Meixner moment invariants for 2D and 3D image recognition. Pattern Recognit Image Anal 28:207–216. https://doi.org/10.1134/S1054661818020128
Xie L, Du C, Zhang C, Soh YC (2002) \(H_{\infty }\) deconvolution filtering of 2D digital systems. IEEE Trans Signal Process 50(9):2319–2332
Roesser R (1975) A discrete state-space model for linear image processing. IEEE Trans Autom Control 20:1–10
Souza CE, Xie L, Coutinho DF (2010) Robust filtering for 2D discrete-time linear systems with convex-bounded parameter uncertainty. Automatica 46:673–681
Wu L, Shi P, Gao H, Wang C (2008) \(H_{\infty }\) filtering for 2D Markovian jump systems. Automatica 44(7):1849–1858
Wei G, Wang Z, Shu H, Fang G (2007) \(H_{\infty }\) deconvolution filter for stochastic systems with interval uncertainties. Circuits Syst Signal Process 26(4):495–512. https://doi.org/10.1007/s00034-007-4004-x
Mesbah A et al (2017) Robust reconstruction and generalized dual Hahn moments invariants extraction for 3D images. 3D Res 8:7. https://doi.org/10.1007/s13319-016-0113-8
Wu H, Coatrieux JL, Shu H (2013) New algorithm for constructing and computing scale invariants of 3D Tchebichef moments. Math Probl Eng 12:1–8
Xu S, Lam J, Zou Y, Lin Z, Paszke W (2005) Robust \(H_{\infty }\) filtering for uncertain 2D continuous systems. IEEE Trans Signal Process 53(5):1731–1738
Zhang B, Lam J, Xu S (2009) Deconvolution filtering for stochastic systems via homogeneous polynomial Lyapunov function. Signal Process 89:605–614
Zouhri A, Boumhidi I (2021) Stability analysis of interconnected complex nonlinear systems using the Lyapunov and Finsler property. Multimed Tools Appl. https://doi.org/10.1007/s11042-020-10449-9
Bruntha PM, Dhanasekar S, Sagayam KM, Pandian SIA (2019) A modified approach for face recognition using PSO and ABC optimization. Int J Innov Technol Explor Eng 8(7):1571–1577
Martin Sagayam K, Narain Ponraj D, Winston Jenkin, Yaspy JC, Esther Jeba D, Clara Antony (2019) Authentication of biometric system using fingerprint recognition with Euclidean distance and neural network classifier. Int J Technol Explor Eng 8(4):766–771
Martin Sagayam K, Jude Hemanth D (2019) A probabilistic model for state sequence analysis in hidden Markov model for hand gesture recognition. Comput Intell 35(1):51–81
Mhathesh TSR, Andrew J, Martin Sagayam K, Henesey L (2021) A 3D Convolutional neural network for bacterial image classification. In: Peter J, Fernandes S, Alavi A (eds) Intelligence in big data technologies-beyond the hype. advances in intelligent systems and computing, vol 1167. Springer, Singapore https://doi.org/10.1007/978-981-15-5285-442
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
BOUKILI, B., EL MALLAHI, M., AMRANI, A. et al. A new approach for \(H_{\infty }\) deconvolution filtering of 2D systems described by the Fornasini–Marchesini and discrete moments. Pattern Anal Applic 25, 63–76 (2022). https://doi.org/10.1007/s10044-021-01030-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10044-021-01030-7