Consistent auto-weighted multi-view subspace clustering

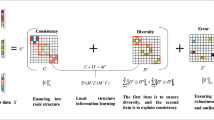
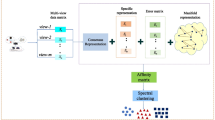
Abstract

Because the data in practical applications usually satisfy the assumption of mixing subspaces and contain multiple features, multi-view subspace clustering has attracted extensive attention in recent years. In previous work, multi-view information can be utilized comprehensively by considering consistency. However, they often treat the information from different views equally. Because it is difficult to ensure that the information of all views is well mined, difficult view will reduce the performance. In this paper, we propose a novel multi-view subspace clustering method named consistent auto-weighted multi-view subspace clustering (CAMVSC) to overcome the above limitation by weighting automatically the representation matrices of each view. In our model, the density and sparsity are both considered to ensure the learning effect of each view. Although simultaneously using the self-representation and the auto-weighting strategy will bring difficulties to solve the model, we successfully design a special updating scheme to obtain the numerical algorithm, and prove its convergence theoretically. Extensive experimental results demonstrate the effectiveness of our proposed method.

Appendix A Proof of Theorems

The Proof of Theorem 1

For presentation purposes, we ignore the superscript of $Z^{(v)}$ for the moment. When we replace the model (11) with the model (13), since $Z_{m:}^{k+1}$ is the optimal solution of the model (13), we can get

$$\begin{aligned} g(\widetilde{Z_{M+1}^k})\le g(\widetilde{Z_M^k}). \end{aligned}$$

(A1)

where $\widetilde{Z_M^k}$ represents the representation matrix which has been updated the first $m-1$-th row in the $k+1$-th iteration, $\widetilde{Z_{M+1}^k}$ represents the representation matrix which has been updated the first m-th row in the $k+1$-th iteration, $g(\widetilde{Z_M^k})$ is the objective function value of $\widetilde{Z_M^k}$ in Eq. (13). Because $a-\frac{a^2}{2b}\le b-\frac{b^2}{2b}$, we have

$$\begin{aligned} \begin{aligned} {\rm Tr}&((F^{k})^T\widetilde{L_{M+1}^k}F^{k})-\frac{{\rm Tr}((F^{k})^T\widetilde{L_{M+1}^k}F^{k})}{2\sqrt{{\rm Tr}((F^{k})^T\widetilde{L_M^k}F^{k})}} \\&\le {\rm Tr}((F^{k})^T\widetilde{L_{M}^k}F^{k})-\frac{{\rm Tr}((F^{k})^T\widetilde{L_{M}^k}F^{k})}{2\sqrt{{\rm Tr}((F^{k})^T\widetilde{L_M^k}F^{k})}}. \end{aligned} \end{aligned}$$

(A2)

By adding (A2) to (A1), we can get

$$\begin{aligned} f(\widetilde{Z_{M+1}^k})\le f(\widetilde{Z_M^k}). \end{aligned}$$

(A3)

where $f(\widetilde{Z_M^k})$ is the objective function value of $\widetilde{Z_M^k}$ in Eq. (11). And since $\widetilde{Z_1^k}=Z^k$, we can get

$$\begin{aligned} f(Z^{k+1})\le f(\widetilde{Z_{N}^k})\le \cdots \le f(\widetilde{Z_2^k})\le f(Z^k). \end{aligned}$$

(A4)

where N denotes the number of samples, so Theorem 1 is proved. $\square$

The Proof of Theorem 2

For $E^{(v)}$, since the optimal solution will minimize the objective function, we can obtain

$$\begin{aligned} \begin{aligned}&\sum _{v=1}^V \left( {\lambda _4^{(v)}}{\Vert {X^{(v)}-X^{(v)}Z^{(v),k}-E^{(v),k+1}}\Vert }_F^2\right. \\&\quad +\left. {\lambda _1^{(v)}}\Vert {E^{(v),k+1}}\Vert _{2,1}\right) \le \\&\sum _{v=1}^V \left( {\lambda _4^{(v)}}{\Vert {X^{(v)}-X^{(v)}Z^{(v),k}-E^{(v),k}}\Vert }_F^2\right. \\&\quad +\left. {\lambda _1^{(v)}}\Vert {E^{(v),k}}\Vert _{2,1}\right) \end{aligned} \end{aligned}$$

(A5)

For F, similarly, by using $a-\frac{a^2}{2b}\le b-\frac{b^2}{2b}$, we can obtain

$$\begin{aligned} \begin{aligned}&{\rm Tr}\left( (F^{k+1})^TL^{(v),k+1}F^{k+1}\right) -\frac{{\rm Tr}\left( (F^{k+1})^TL^{(v),k+1}F^{k+1}\right) }{2\sqrt{{\rm Tr}((F^{k})^TL^{(v),k+1}F^{k}})}\le \\&{\rm Tr}\left( (F^{k})^TL^{(v),k+1}F^{k}\right) -\frac{{\rm Tr}((F^{k})^TL^{(v),k+1}F^{k})}{2\sqrt{{\rm Tr}((F^{k})^TL^{(v),k+1}F^{k}})}. \end{aligned} \end{aligned}$$

(A6)

where $v=1, \ldots , V$. According to the model (16), we know that $\phi (F^{k+1})\le \phi (F^{k})$, where $\phi (F^{k})$ denotes the objective function value of F with the k-th iteration in the model (16). Utilizing $\alpha ^{(v),k}=\frac{1}{2\sqrt{{\rm Tr}((F^k)^T)L^{(v),k+1}F^{k}}}$, we can get

$$\begin{aligned} \begin{aligned} \sum _{v=1}^V&\alpha ^{(v),k}{{\rm Tr}\left( (F^{k+1})^TL^{(v),k+1}F^{k+1}\right) }\le \\&\sum _{v=1}^V\alpha ^{(v),k}{{\rm Tr}((F^{k})^TL^{(v),k+1}F^{k})}. \end{aligned} \end{aligned}$$

(A7)

Adding (A7) to (A6), we can obtain

$$\begin{aligned}&\sum _{v=1}^V \sqrt{{{\rm Tr}((F^{k+1})^TL^{(v),k+1}F^{k+1})}}\nonumber \\&\quad \le \sum _{v=1}^V\sqrt{{{\rm Tr}((F^{k})^TL^{(v),k+1}F^{k})}}. \end{aligned}$$

(A8)

Hence, by updating $Z^{(v)}$, $E^{(v)}$ and F step by step, we can obtain

$$\begin{aligned} \begin{aligned} \sum _{v=1}^V&({\lambda _4^{(v)}}{\Vert {X^{(v)}-X^{(v)}Z^{(v),k+1}-E^{(v),k+1}}\Vert }_F^2\\&+{\lambda _3^{(v)}}\Vert {Z^{(v),k+1}}\Vert _F^2+{\lambda _2^{(v)}}\Vert {Z^{(v),k+1}}\Vert _1\\&+{\lambda _1^{(v)}}\Vert {E^{(v),k+1}}\Vert _{2,1} +\sqrt{{\rm Tr}((F^{k+1})^TL^{(v),k+1}F^{k+1})})\le \\ \sum _{v=1}^V&({\lambda _4^{(v)}}{\Vert {X^{(v)}-X^{(v)}Z^{(v),k}-E^{(v),k}}\Vert }_F^2 +{\lambda _3^{(v)}}\Vert {Z^{(v),k}}\Vert _F^2\\&+{\lambda _2^{(v)}}\Vert {Z^{(v),k}}\Vert _1+{\lambda _1^{(v)}}\Vert {E^{(v),k}}\Vert _{2,1}+\sqrt{{\rm Tr}((F^{k})^TL^{(v),k}F^{k})}). \end{aligned} \end{aligned}$$

(A9)

Hence, $\varphi (Z^{(v),k+1},E^{(v),k+1},F^{k+1})\le \varphi (Z^{(v),k},E^{(v),k},F^{k})$. Theorem 2 is proved. In summary, CAMVSC is also convergent in theory. $\square$