Abstract
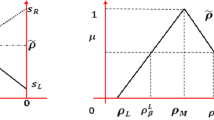
This paper considers a two-warehouse fuzzy-stochastic mixture inventory model involving variable lead time with backorders fully backlogged. The model is considered for two cases—without and with budget constraint. Here, lead-time demand is considered as a fuzzy random variable and the total cost is obtained in the fuzzy sense. The total demand is again represented by a triangular fuzzy number and the fuzzy total cost is derived. By using the centroid method of defuzzification, the total cost is estimated. For the case with fuzzy-stochastic budget constraint, surprise function is used to convert the constrained problem to a corresponding unconstrained problem in pessimistic sense. The crisp optimization problem is solved using Generalized Reduced Gradient method. The optimal solutions for order quantity and lead time are found in both cases for the models with fuzzy-stochastic/stochastic lead time and the corresponding minimum value of the total cost in all cases are obtained. Numerical examples are provided to illustrate the models and results in both cases are compared.


Similar content being viewed by others
References
Ben-Daya M, Raouf A (1994) Inventory models involving lead time as decision variable. J Oper Res Soc 45:579–582
Bhunia AK, Maiti M (1998) A two-warehouse inventory model for deteriorating items with a linear trend in demand and shortages. J Oper Res Soc 49:287–292
Charnes A, Cooper W (1959) Chance constrained programming. Manag Sci 6:73–79
Chang HC, Yao J-S, Ouyang LY (2006a) Fuzzy mixture inventory model involving fuzzy random variable lead time demand and fuzzy total demand. Eur J Oper Res 169:65–80
Chang HC, Ouyang LY, Wu KS, Ho CH (2006b) Integrated vendor-buyer cooperative inventory models with controllable lead time and ordering cost reduction. Eur J Oper Res 170:481–495
Hartely VR (1976) Operations research—a managerial emphasis. Good Year, Santa Monica, CA, pp 315–317 (Chapter 12)
Huq F, Cutright K, Jones VA, Hensler DA (2006) Simulation study of a two level warehouse inventory replenishment system. Int J Phys Distrib Logist Manag 36:51–65
Kar S, Bhunia AK, Maiti M (2001) Deterministic inventory model with two levels of storage, a linear trend in demand and a fixed time horizon. Comput Oper Res 28:1315–1331
Kaufmann A, Gupta MM (1991) Introduction to fuzzy arithmetic: theory and applications. Van Nostrand Reinhold, New York
Liao CJ, Shyu CH (1991) An analytical determination of lead time with normal demand. Int J Oper Prod Manag 11:72–78
Liu B, Iwamura KB (1998a) Chance constraint programming with fuzzy parameters. Fuzzy Sets Syst 94:227–237
Liu B, Iwamura KB (1998b) A note on chance constrained programming with fuzzy coefficients. Fuzzy Sets Syst 100:229–233
Maiti MK, Maiti M (2006) Fuzzy inventory model with two warehouses under possibility constraints. Fuzzy Sets Syst 157:52–73
Maiti MK, Maiti M (2007) Two storage inventory model with lot size dependent fuzzy lead time under possibility constraints via genetic algorithm. Eur J Oper Res 179:352–371
Naddor E (1966) Inventory system. Wiley, New York
Neumaier A (2003) Fuzzy modeling in terms of surprise. Fuzzy Sets Syst 135:21–38
Ouyang LY, Yeh NC, Wu KS (1996) Mixture inventory model with backorders and lost sales for variable lead time. J Oper Res Soc 47:829–832
Ouyang LY, Chuang BR (2000) A periodic review inventory model involving variable lead time with a service level constraint. Int J Syst Sci 31:1209–1215
Ouyang LY, Yao JS (2002) A minimax distribution free procedure for mixed inventory model involving variable lead time with fuzzy demand. Comput Oper Res 29:471–487
Puri ML, Ralescu DA (1986) Fuzzy random variable. J Math Anal Appl 114:409–422
Rong M, Mahapatra NK, Maiti M (2008a) A two warehouse inventory model for a deteriorating item with partially/fully backlogged shortage and fuzzy lead time. Eur J Oper Res 189:59–75
Rong M, Mahapatra NK, Maiti M (2008b) A multi-objective wholesaler-retailers inventory-distribution model with controllable lead-time based on probabilistic fuzzy set and triangular fuzzy number. Appl Math Model 32:2670–2685
Rong M, Maiti M (2010) A two warehouse inventory model for a with stochastic demand, controllable lead time and fuzzy present value: a technique to deal with arbitrary fuzzy number. Int J Oper Res 8:208–229
Sarma KVS (1987) A deterministic order-level inventory model for deteriorating items with two storage facilities. Eur J Oper Res 29:70–72
Silver EA, Peterson R (1985) Decision systems for inventory management and production planning. Wiley, New York
Tersine RJ (1982) Principle of inventory and materials management. North-Holland, New York
Wu KS, Ouyang LY, Ho CH (2007) Integrated vendor-buyer inventory system with sublot sampling inspection policy and controllable lead time. Int J Syst Sci 38:339–350
Zhou YW, Yang SL (2003) A two-warehouse inventory model for items with stock-level-dependent demand rate. Int J Prod Econ 95:215–228
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1
Remark 1
If per unit holding cost at \(RW\) and \(OW\) are same (i.e. \(h_1 = h_2 = h\), say) then the total average holding cost expression is same with the holding cost expression of single warehouse EOQ model for the same order quantity.
Proof
Appendix 2
Appendix 3 (Markov inequality)
Again, \(\int \nolimits _{B+pX\ge p(Q+r)} {\left({\frac{B+pX}{p(Q+r)}} \right)f(x)} dx\ge \int \nolimits _{B+pX\ge p(Q+r)} {f(x)} dx\)
We have
Appendix 4
Rights and permissions
About this article
Cite this article
Panda, D., Rong, M. & Maiti, M. Fuzzy mixture two warehouse inventory model involving fuzzy random variable lead time demand and fuzzy total demand. Cent Eur J Oper Res 22, 187–209 (2014). https://doi.org/10.1007/s10100-013-0284-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10100-013-0284-9