Abstract
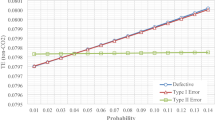
We consider the effects of inspection and repair stations on the production capacity and product quality in a serial garments production line with possible inspection and repair following each operation. We construct a profit function that takes into account inspection, repair, scrap, and goodwill costs, as well as the capacity of each station. Then we discuss how the profit function can be maximized and provide properties of the optimal inspection plan. Our analysis captures the possibility of increasing production capacity by scrapping or repairing defective items before a bottleneck operation station, and hence reducing the waste of operation capacity on defective products. Our numerical results show that incorporating such capacity considerations can have substantial impact on the optimal inspection policy and that optimal inspection allocations can be identified quickly even for large problem instances.






Similar content being viewed by others
References
Bai DS, Yun HJ (1996) Optimal allocation of inspection effort in a serial multi-stage production system. Comput Ind Eng 30(3):387–396
Britney RR (1972) Optimal screening plans for nonserial production systems. Manag Sci 18:550–559
Chang PC, Lin YK (2015) Reliability analysis for an apparel manufacturing system applying fuzzy multistate network. Comput Ind Eng 88:458–469
Chen A (1998) An alternative dynamic programming approach to allocating inspection points in multistage production systems. Qual Eng 11(2):197–205
Chevalier PB, Wein LM (1997) Inspection for circuit board assembly. Manag Sci 43:1198–1213
Cochran JK, Erol R (2001) Performance modeling of serial production lines with inspection/repair stations. Int J Prod Res 39:1707–1720
Foster JW, Malave CO, Villalobos JR (1990) Flexible inspection within an aggregated information environment. Comput Ind Eng 19:224–228
Gopalakrishnan D, Nayak A. Defects in garments http://www.fibre2fashion.com/industry-article/3092/defects-in-garments. Accessed 20 Jun 2018
Hossain SJ (2016) Optimal configuration of inspection and rework stations in a multistage flexible flowline. Master’s thesis, Louisiana State University
Hurst EG (1973) Imperfect inspection in a multistage production process. Manag Sci 20:378–384
Kakade V, Jorge FV, Smith JS (2004) An optimization model for selective inspection in serial manufacturing systems. Int J Prod Res 42(18):3891–3909
Kim J, Gershwin SB (2005) Integrated quality and quantity modeling of a production line. OR Spectrum 27:287–314
Kouikoglou VS, Phillis YA (2002) Design of product specifications and control policies in a single-stage production system. IIE Trans 34:591–600
Lindsay GF, Bishop AB (1964) Allocation of screening inspection efforts—a dynamic programming approach. Manag Sci 10:342–352
LLC The Optimization Firm (2017) GAMS-documentation. https://www.gams.com/latest/docs/gams.pdf. Accessed 8 Nov 2018
Mandroli SS, Shrivastava AK, Ding Y (2006) A survey of inspection strategy and sensor distribution studies in discrete-part manufacturing processes. IIE Trans 38:309–328
Mok PY, Cheung TY, Wong WK, Leung SYS, Fan JT (2013) Intelligent production planning for complex garment manufacturing. J Intell Manuf 24(1):133–145
Penn M, Raviv T (2008) A polynomial time algorithm for solving a quality control station configuration problem. Discrete Appl Math 156:412–419
Ramzan MB, Kang CW (2016) Minimization of inspection cost by determining the optimal number of quality inspectors in the garment industry. Indian J Fibre Text Res 41(3):346–350
Rau H, Chu YH (2005) Inspection allocation planning with two types of workstations: WVD and WAD. Int J Adv Manuf Technol 25:947–953
Rau H, Chu YH, Cho KH (2005) Layer modeling for the inspection allocation problem in re entrant production systems. Int J Prod Res 43(17):3633–3655
Raviv T (2013) An efficient algorithm for maximizing the expected profit from a serial production line with inspection stations and rework. OR Spectrum 35(3):609–638
Raz T (1986) A survey of models for allocating inspection effort in multistage production systems. J Qual Technol 18:239–247
Raz T, Kaspi M (1991) Location and sequencing of imperfect inspection operations in serial multi-stage production systems. Int J Prod Res 29:1645–1659
Shetwan AG, Vitanov VI, Tjahjono B (2011) Allocation of quality control stations in multistage manufacturing systems. Comput Ind Eng 60(4):473–484
Shin WS, Hart SM, Lee HF (1995) Strategic allocation of inspection stations for flow assembly line: a hybrid procedure. IIE Trans 27:707–715
Villalobos JR, Foster JW, Disney RL (1993) Flexible inspection systems for serial multi-stage production systems. IIE Trans 25:16–26
Yuen CWM, Wong WK, Qian SQ, Chan LK, Fung EHK (2009) A hybrid model using genetic algorithm and neural network for classifying garment defects. Expert Syst Appl 36(2):2037–2047
Acknowledgements
This research was supported by the National Science Foundation under Grants CMMI-0856600 and CMMI-1536990. We would like to thank two anonymous referees for their insightful comments that led to substantial improvements to this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendices
A Notation
In this appendix, we provide the notation used throughout the paper as a reference, see Table 3.
B Nonlinear Program for the General Model
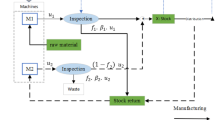
In this appendix, we formulate the nonlinear program for the general model where any station can be the bottleneck. Decision variables are the inspection plan \(a_i\), \(i=1,\ldots ,N\), and the flow rates throughout the production line (i.e., \(\lambda _i\), \(\lambda _i^R\) for \(i=1,\ldots ,N\), and \(\lambda _{N+1}\)) given the incoming defect information \(\pi _{1,j}^O\) for all j.
The objective \(T_P\) is the general total profit rate function. The constraints (33)–(38) represent balance equations for the flow in the system, allowing only the repair stations to become unstable. The constraint (39) is needed because some of the model parameters depend on the decision variables.
Let the solution be given by \(\bar{a}_i, \bar{\lambda }_i\), and \(\bar{\lambda }_i^R\) for \(i=1,\ldots ,N\), as well as \(\bar{\lambda }_{N+1}\). Then the repair station \(R_i\) is stable if \(\bar{\lambda }_i \bar{a}_i r_{i} \le \mu _i^R\) and unstable if \(\bar{\lambda }_i \bar{a}_i r_{i}>\mu _i^R\) in the allocation scenario that maximizes the return. We also reject at the rate \(\nu _{0}= \lambda -\bar{\lambda }_1\) at the dummy operation node \(O_0\), and stages i with \(\bar{a}_i=1\) are assigned an inspection station.
C Model Construction for Sect. 6.1
In this appendix, we formulate the profit rate function \(T_P\) depending on the inspection strategy and the input parameters, \(\lambda ,R, C_i, G_i, H_i\), and \(U_i\), \(i=1,2\). Let \(\mu _1^O=\mu _1\) and \(\mu _2^O=\mu _2\) denote the processing capacities at stations 1 and 2, respectively. We consider the case with \(\mu _1^I,\)\(\mu _2^I \ge \lambda \), so that the inspection operations never constrain the system. The throughput \(\lambda _{N+1}\) of the system is denoted by \(\mu \).
The optimal inspection locations are determined based on the NLP (25)–(32). Since all defects are major, we have \(s_i=p_i\) and \(r_{i}=0\) for \(i=1,2\). Moreover, \(E_i^O=C_i\), \(E_i^I=H_i\), \(\pi _{1,1}^O=0\), \(\pi _{1,1}^I=p_1\), \(\pi _{1,2}^O=\pi _{1,2}^I=0\), \(\pi _{2,1}^O=\pi _{2,1}^I=p_1(1-a_1)\), \(\pi _{2,2}^O=0\), \(\pi _{2,2}^I=p_2\), and \(\pi _{3,j}^O=p_j(1-a_j)\) for \(i=1,2\) and \(j=1,2\). Hence the NLP (25)–(32) becomes
Note that in the above allocation NLP, all quantities are known except for the decision variables \(a_1\), \(a_2\) and the throughput \(\mu \). The goodwill cost in the objective function (40) results from the fact that goodwill costs for different defects are additive.
Since the problem size is small, we can easily solve the NLP in (40)–(44) by enumerating all four possible solutions and obtain the profit function \(T_P(a_1,a_2)\). In particular, considering the nontrivial case where the profit functions are nonnegative, we have
Next, we provide the total profit functions for the input and capacity constrained systems. We start with the case where the system is constrained by the arrival rate, so that \(\lambda < \min \{\mu _1,\mu _2\}\). In this case, we cannot see the side benefit of having inspection before the bottleneck on the optimal decision and our inspection allocation decision agrees with traditional wisdom in that we choose to inspect whenever the expected inspection cost for a unit is less than the expected cost of not inspecting (see, e.g., Bai and Yun 1996; Chen 1998; Hurst 1973; Lindsay and Bishop 1964; Raz and Kaspi 1991). More specifically, rearranging the profit functions (45)–(48), we obtain
where \((H_i+p_iR+p_iU_i)\), \(i=1,2\), can be considered as the expected cost of inspection for defect i only per unit, and \([H_1+p_1U_1+(H_2+p_2U_2)(1-p_1)+(p_1+p_2-p_1p_2)R]\) as the expected cost of inspection when inspecting both defects simultaneously. Similarly, \(p_1(C_2+p_2G_2+G_1)\), \(p_2(p_1G_1+G_2)\), \((p_1G_1+p_2G_2+p_1C_2)\) can be viewed as the expected cost of not inspecting at locations 1, 2, and 1 and 2 together, respectively.
Next we derive the profit functions for the interesting case where the production line is constrained by the capacity of the second operation station having processing rate \(\mu _2\), assuming that \(\mu _1>\lambda >\mu _2/(1-p_1)\). The first condition ensures that \(O_1\) is not a bottleneck, and the second condition ensures that we have in all cases enough input for \(O_2\) to be a bottleneck. Hence, as a result of Theorem 1, we reject any incoming job with probability \([\lambda -\mu _2/(1-p_1a_1)]/\lambda \) to stabilize the system. In this case, we can observe the effects of throughput considerations on the inspection allocation decision. Note that by inspecting for defect 1 after the first operation station and scrapping defective items, we not only remove the defective items but also increase the capacity of the production line from \(\mu _2\) to \(\mu _2/(1-p_1)\). Thus, in the capacity constrained case, inspecting after the first operation has gained an advantage with magnitude depending on the value of \(p_1\). We will see that even under the same defect distribution and cost parameters, inspecting after operation station 1 for defect 1 becomes more beneficial as compared to the first case. Similar to the first case, we can compare all three different inspection decisions to the no inspection case using the profit functions (45)–(48) to obtain
The profit function (\(T_P\)) formulation and the pairwise profit comparisons obtained in this appendix can be used to identify the optimal inspection decisions in the examples of Sect. 6.1.
Rights and permissions
About this article
Cite this article
Tekin, S., Andradóttir, S. Inspection location in capacity-constrained lines. Cent Eur J Oper Res 28, 905–937 (2020). https://doi.org/10.1007/s10100-018-00604-x
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10100-018-00604-x