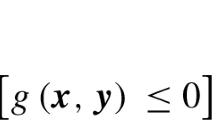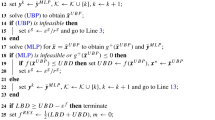Skip to main content
SpringerLink
Log in

Global solution of semi-infinite programs

  • Published:
Mathematical Programming Submit manuscript

Abstract.

Optimization problems involving a finite number of decision variables and an infinite number of constraints are referred to as semi-infinite programs (SIPs). Existing numerical methods for solving nonlinear SIPs make strong assumptions on the properties of the feasible set, e.g., convexity and/or regularity, or solve a discretized approximation which only guarantees a lower bound to the true solution value of the SIP. Here, a general, deterministic algorithm for solving semi-infinite programs to guaranteed global optimality is presented. A branch-and-bound (B&B) framework is used to generate convergent sequences of upper and lower bounds on the SIP solution value. The upper-bounding problem is generated by replacing the infinite number of real-valued constraints with a finite number of constrained inclusion bounds; the lower-bounding problem is formulated as a convex relaxation of a discretized approximation to the SIP. The SIP B&B algorithm is shown to converge finitely to ɛ−optimality when the subdivision and discretization procedures used to formulate the node subproblems are known to retain certain convergence characteristics. Other than the properties assumed by globally-convergent B&B methods (for finitely-constrained NLPs), this SIP algorithm makes only one additional assumption: For every minimizer x* of the SIP there exists a sequence of Slater points xn for which (cf. Section 5.4). Numerical results for test problems in the SIP literature are presented. The exclusion test and a modified upper-bounding problem are also investigated as heuristic approaches for alleviating the computational cost of solving a nonlinear SIP to guaranteed global optimality.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Alefeld, G., Mayer, G.: Interval analysis: theory and applications. J. Comput. Appl. Math. 121, 421–464 (2000)

    Article  Google Scholar 

  2. Baumann, E.: Optimal centered forms. BIT 28, 80–87 (1988)

    Google Scholar 

  3. Bhattacharjee, B.: Kinetic Model Reduction using Integer and Semi-Infinite Programming. PhD thesis, Massachusetts Institute of Technology, Cambridge, Massachusetts, December 2003

  4. Bhattacharjee, B., Green, W.H. Jr., Barton, P.I.: Interval methods for semi-infinite programs. Comput. Optim. Appl. 30 (1), 63–94 (2005)

    Article  Google Scholar 

  5. Coope, I.D., Watson, G.A.: Projected Lagrangian algorithm for semi-infinite programming. Math. Program. 32, 337–256 (1985)

    Article  Google Scholar 

  6. Gill, P.E., Murray, W., Saunders, M.A., Wright, M.H.: User’s Guide for NPSOL 5.0: A FORTRAN Package for Nonlinear Programming. 1998

  7. Hettich, R., Kortanek, K.O.: Semi-infinite programming: Theory, methods and applications. SIAM Review 35, 380–429 (1993)

    Article  Google Scholar 

  8. Horst, R.: A general class of branch-and-bound methods in global optimization with some new approaches for concave minimization. J. Optim. Theory Appl. 51, 271–291 (1986)

    Article  Google Scholar 

  9. Horst, R.: Deterministic global optimization with partition sets whose feasibility is not known: Application to concave minimization, reverse convex constraints, DC-programming,and Lipschitzian optimization. J. Optim. Theory Appl. 58, 11–37 (1988)

    Article  Google Scholar 

  10. Horst, R., Tuy, H.: Global Optimization: Deterministic approaches. Springer-Verlag, 1996. 3rd Edition

  11. McCormick, G.P.: Computability of global solutions to factorable nonconvex programs: Part I: Convex underestimating problems. Math. Program. 10, 147–175 (1976)

    Article  Google Scholar 

  12. Moore, R.: Methods and Applications of Interval Analysis. SIAM, Philadelphia PA, 1979

  13. Polak, E.: Optimization Algorithms and Consistent Approximations. Springer-Verlag, New York, New York, 1997

  14. Ratschek, H., Rokne, J.: Computer Methods for the Range of Functions. Ellis Horwood Limited, Chichester, England, 1984

  15. Reemsten, R., Gorner, S.: Numerical methods for semi-infinite programming: A survey. In: R. Reemsten, J. Ruckmann (eds.), Semi-infinite Programming, Kluwer Academic Publishers, Dordrecht, Netherlands, 1998, pp. 195–275

  16. Singer, A.B.: LibBandB.a Version 3.1 Manual. Massachusetts Institute of Technology, Cambridge, MA, 2003

  17. Singer, A.B., Barton, P.I.: Global Solution of Optimization Problems with Parameter-Embedded Linear Dynamic Systems. J. Optim. Theory Appl. 121 (3), 613–646 (2004)

    Article  Google Scholar 

  18. Stein, O.: Bi-level Strategies in Semi-infinite Programming. Kluwer, 2003

  19. Still, G.: Generalized semi-infinite programming: Theory and Methods. European J. Oper. Res. 119, 303–313 (1999)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Dept. of Chemical Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA, USA

    B. Bhattacharjee, P. Lemonidis, W.H. Green Jr. & P.I. Barton

Authors
  1. B. Bhattacharjee
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. P. Lemonidis
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. W.H. Green Jr.
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. P.I. Barton
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to P.I. Barton.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Bhattacharjee, B., Lemonidis, P., Green Jr., W. et al. Global solution of semi-infinite programs. Math. Program. 103, 283–307 (2005). https://doi.org/10.1007/s10107-005-0583-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10107-005-0583-6

Mathematics Subject Classification (2000):

Search

Navigation