Skip to main content
Springer Nature Link
Log in

The constrained minimum weighted sum of job completion times problem

  • Published:
Mathematical Programming Submit manuscript

Abstract

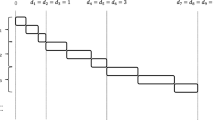
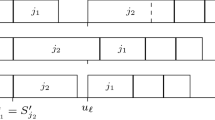
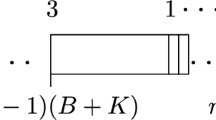
We consider the problem of minimizing the weighted sum of job completion times on a single machine (subject to certain job weights) with an additional side constraint on the weighted sum of job completion times (with respect to different job weights). This problem is NP-hard, and we provide a polynomial time approximation scheme for this problem. Our method is based on Lagrangian relaxation mixed with carefully guessing the positions of certain jobs in the schedule.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Aslam, J.A., Rasala, A., Stein, C., Young, N.E.: Improved bicriteria existence theorems for scheduling. In: Proceedings of the 10th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA'1999), 1999, pp. 846–847

  2. Cole, R.: Slowing down sorting networks to obtain faster sorting algorithms. J. ACM 34, 200–208 (1987)

    Article  MathSciNet  Google Scholar 

  3. Garey, M.R., Johnson, D.S.: Computers and Intractability. Freeman, San-Francisco, 1979

  4. Goemans, M.X., Ravi, R.: The constrained minimum spanning tree problem. Proceedings of the 5th Scandinavian Workshop on Algorithm Theory (SWAT'1996). LNCS 1097, Springer Verlag, 1996, pp. 66–75

  5. Goemans, M., Williamson, D.P.: Two-dimensional Gantt charts and a scheduling algorithm of Lawler. SIAM J. Discrete Math. 13, 281–294 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  6. Horn, W.A.: Single-machine job sequencing with tree-like precedence ordering and linear delay penalties. SIAM J. Appl. Math. 23, 189–202 (1972)

    Article  MATH  MathSciNet  Google Scholar 

  7. Hassin, R.: Approximation schemes for the restricted shortest path problem. Math. Oper. Res. 17, 36–42 (1992)

    MATH  MathSciNet  Google Scholar 

  8. Levin, A.: A strongly polynomial-time approximation for a class of bicriteria problems. Oper. Res. Lett. 32, 530–534 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  9. Lin, J.-H., Vitter, J.S.: ɛ-approximations with minimum packing violation. Proceedings of the 24th Annual ACM Symposium on the Theory of Computing (STOC'1992), 1992, pp. 771–782

  10. Marathe, M.V., Ravi, R., Sundaram, R., Ravi, S.S., Rosenkrantz, D.J., Hunt H.B. III: Bicriteria network design problems. J. Algorithms 28, 142–171 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  11. McCormick, S.T., Pinedo, M.L.: Scheduling n independent jobs on m uniform machines with both flowtime and makespan objectives: a parametric analysis. ORSA J. Comput. 7, 63–77 (1995)

    MATH  Google Scholar 

  12. Megiddo, N.: Combinatorial optimization with rational objective functions. Math. Oper. Res. 4, 414–424 (1979)

    MATH  MathSciNet  Google Scholar 

  13. Queyranne, M.: Structure of a simple scheduling polyhedron. Math. Program. 58, 263–285 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  14. Queyranne, M., Wang, Y.: Single-machine scheduling polyhedra with precedence constraints. Math. Oper. Res. 16, 1–20 (1991)

    Article  MATH  MathSciNet  Google Scholar 

  15. Rasala, A., Stein, C., Torng, E., Uthaisombut, P.: Existence theorems, lower bounds and algorithms for scheduling to meet two objectives. In: Proceedings of the 13th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA'2002), 2002, pp. 723–731

  16. Ravi, R.: Bicriteria spanning tree problems. Proceedings of the 5th Workshop on Approximation Algorithms for Combinatorial Optimization (APPROX'2002). LNCS 2462, Springer Verlag, 2002, pp. 3–4

  17. Shmoys, D.B., Tardos, E.: An approximation algorithm for the generalized assignment problem. Math. Program. 62, 461–474 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  18. Smith, W.E.: Various optimizers for single-stage production. Naval Research Logistics Quarterly 3, 59–66 (1956)

    MathSciNet  Google Scholar 

  19. Stein, C., Wein, J.: On the existence of schedules that are near-optimal for both makespan and total-weighted completion time. Oper. Res. Lett. 21, 115–122 (1997)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Statistics, The Hebrew University, Jerusalem, 91905, Israel

    Asaf Levin

  2. Department of Mathematics, University of Twente, P.O. Box 217, 7500, AE, Enschede, The Netherlands

    Gerhard J. Woeginger

  3. Department of Mathematics and Computer Science, TU Eindhoven, P.O. Box 513, 5600, MB, Eindhoven, The Netherlands

    Gerhard J. Woeginger

Authors
  1. Asaf Levin
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Gerhard J. Woeginger
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Asaf Levin.

Additional information

An earlier version of this paper appeared in the Proceedings of the 10th International IPCO Conference.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Levin, A., Woeginger, G. The constrained minimum weighted sum of job completion times problem. Math. Program. 108, 115–126 (2006). https://doi.org/10.1007/s10107-005-0691-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10107-005-0691-3

Keywords