Abstract
For any ɛ > 0 we give a (2 + ɛ)-approximation algorithm for the problem of finding a minimum tree spanning any k vertices in a graph (k-MST), improving a 3-approximation algorithm by Garg [10]. As in [10] the algorithm extends to a (2 + ɛ)-approximation algorithm for the minimum tour that visits any k vertices, provided the edge costs satisfy the triangle inequality.
Similar content being viewed by others
References
Agrawal, A., Klein, P., Ravi, R.: When trees collide: An approximation algorithm for the generalized Steiner problem on networks. SIAM J. Comput, 24 (3), 440–456 (1995)
Archer, A., Williamson, D.P.: Faster approximation algorithms for the minimum latency problem. In: Proceedings of 14th ACM-SIAM Symp. on Discrete Algorithms (SODA), 2003, pp. 88–96
Arora, S.: Polynomial-time approximation schemes for Euclidean TSP and other geometric problems. J. ACM 45 (5), 1–30, (1998) Preliminary versions in Proceedings of 37th IEEE Symp. on Foundations of Computer Science (FOCS), pp. 2–12, 1996, and in Proceedings of 38th IEEE Symp. on Foundations of Computer Science (FOCS), 1997, pp. 554–563
Arya, S., Ramesh, H.: 2.5-factor approximation algorithm for the k-MST problem. Information Processing Letters 65 (3), 117–118 (1998)
Awerbuch, B., Azar, Y., Blum, A., Vempala, S.: New approximation guarantees for minimum weight k-trees and prize-collecting salesmen. SIAM J. Comput. 28 (1), 254–262 (1998)
Blum, A., Chalasani, P., Coppersmith, D., Pulleyblank, B., Raghavan, P., Sudan, M.: The minimum latency problem. In: Proceedings of 26th ACM Symp. on Theory Of Computing (STOC), 1994, pp. 163–171
Blum, A., Ravi, R., Vempala, S.: A constant factor approximation for the k-MST problem. J. Comput. Syst. Sci. 58 (1), 101–108 (1999)
Chaudhuri, K., Godfrey, B., Rao, S., Talwar, K.: Paths, trees and minimum latency tours. In: Proceedings of 44th IEEE Symp. on Foundations of Computer Science (FOCS), 2003, pp. 36–45
Fischetti, M., Hamacher, H.W., Jörnsten, K., Maffioli, F.: Weighted k-cardinality trees: complexity and polyhedral structure. Networks 24, 11–21 (1994)
Garg, N.: A 3-approximation for the minimum tree spanning k vertices. In: Proceedings of 37th IEEE Symp. on Foundations of Computer Science (FOCS), 1996, pp. 302–309
Garg, N.: Saving an ɛ: a 2-approximation for the k-MST problem in graphs. In: Proceedings of 37th ACM Symposium on Theory of Computing (STOC), 2005 pp. 396–402
Goemans, M., Kleinberg, J.: An improved approximation ratio for the minimum latency problem. Math. Prog. 82, 111–124 (1998)
Goemans, M., Williamson, D.: A general approximation technique for constrained forest problems. SIAM J. Comput. 24 (2), 296–317 (1995)
Hockbaum, D.: Approximation algorithms for
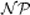 -hard problems. PWS Publishing Company, 1997
-hard problems. PWS Publishing Company, 1997Mitchell, J.S.B.: Guillotine subdivisions spproximate polygonal subdivisions: A simple polynomial-time approximation scheme for geometric TSP, k-MST, and related problems. SIAM J. Comput. 28 (4), 1298–1309 (1999)
Rajagopalan, S., Vazirani, V.V.: Logarithmic approximation of minimum weight k-trees. Unpublished manuscript, 1995
Ravi, R., Sundaram, R., Marathe, M., Rosenkrantz, D., Ravi, S.: Spanning trees short and small. SIAM J. Disc. Math. 9 (2), 178–200 (1996)
Vazirani, V.V.: Approximation algorithms. Springer-Verlag, 2001
Zelikovsky, A., Lozevanu, D.: Minimal and bounded trees. In: Tezele Cong. XVIII Acad. Romano-Americane, 1993, pp. 25–26
Author information
Authors and Affiliations
Corresponding author
Additional information
Research supported by NSF CAREER award NSF CCR-9502747, NSF grants CCR-0205594 and CCR-0098180, an Alfred Sloan Fellowship, and a Packard Fellowship.
Research supported by an NSERC Discovery grant.
Rights and permissions
About this article
Cite this article
Arora, S., Karakostas, G. A 2 + ɛ approximation algorithm for the k-MST problem. Math. Program. 107, 491–504 (2006). https://doi.org/10.1007/s10107-005-0693-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-005-0693-1





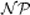 -hard problems. PWS Publishing Company, 1997
-hard problems. PWS Publishing Company, 1997