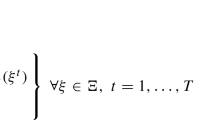Abstract
An important question in discrete optimization under uncertainty is to understand the persistency of a decision variable, i.e., the probability that it is part of an optimal solution. For instance, in project management, when the task activity times are random, the challenge is to determine a set of critical activities that will potentially lie on the longest path. In the spanning tree and shortest path network problems, when the arc lengths are random, the challenge is to pre-process the network and determine a smaller set of arcs that will most probably be a part of the optimal solution under different realizations of the arc lengths. Building on a characterization of moment cones for single variate problems, and its associated semidefinite constraint representation, we develop a limited marginal moment model to compute the persistency of a decision variable. Under this model, we show that finding the persistency is tractable for zero-one optimization problems with a polynomial sized representation of the convex hull of the feasible region. Through extensive experiments, we show that the persistency computed under the limited marginal moment model is often close to the simulated persistency value under various distributions that satisfy the prescribed marginal moments and are generated independently.
Similar content being viewed by others
References
Atamturk, A.: Strong formulations of robust mixed 0-1 integer programming. To appear in Math. Prog. (2005)
Bertsimas, D., Popescu, I.: Optimal inequalities in probability: A convex optimization approach. SIAM J. Optim. 15, No. 3, 780–804 (2005)
Bertsimas, D., Popescu, I.: On the relation between option and stock prices: An optimization approach. Oper. Res. 50, No. 2, 358–374 (2002)
Bertsimas, D., Natarajan K., Chung Piaw Teo.: Tight bounds on expected order statistics. To appear in Probability in Engineering and Informational Sciences (2005)
Bertsimas, D., Natarajan, K., Chung Piaw Teo: Tight bounds on expected order statistics. Working Paper (2005)
Bertsimas, D., Sim, M.: Robust discrete optimization and network flows. Math. Prog. 98, No. 1–3, 49–71 (2003)
Boyd, S., Vandenberghe, L.: Convex Optimization. Cambridge University Press (2003)
Kleindorfer, G. B.: Bounding distributions for stochastic acyclic networks. Oper. Res. 19, No. 6, 1586–1601 (1971)
Klein Haneveld, W. K.: Robustness against dependence in PERT: An application of duality and distributions with known marginals. Math. Prog. Study 27, 153–182 (1986)
Kojima, M., Kim, S., Waki, H.: A general framework for convex relaxation of polynomial optimization problems over cones. Journal of Operations Research Society of Japan 46, No. 2, 125–144 (2003)
Kouvelis, P., Yu, G.: Robust discrete optimization and its applications. Kluwer Academic Publishers, Norwell, MA (1997)
Lasserre, J. B.: Bounds on measures satisfying moment conditions. Ann. Appl. Prob. 12, 1114–1137 (2002)
Lawler, E. L.: Combinatorial Optimization: Networks and Matroids (1976)
Magnanti, T. L., Wolsey, L. A.: Optimal Trees. Network Models: Handbooks in Operations Research and Management Science 7, 503–615 (1995)
Malcolm, D. G., Roseboom, J. H., Clark, C. E., Fazar, W.: Application of a technique for research and development program evaluation. Oper. Res. 7, 646–669 (1959)
Meilijson, I., Nadas, A.: Convex majorization with an application to the length of critical path. J. Appl. Prob. 16, 671–677 (1979)
Nadas, A.: Probabilistic PERT. IBM Journal of Research and Development 23, 339–347 (1979)
Sturm, J. F.: SeDuMi v. 1.03, Available from http://fewcal.kub.nl/sturm/software/sedumi.html.
Van Slyke, R. M.: Monte Carlo methods and the PERT problem. Oper. Res. 11, 839–860 (1963)
Yaman, H., Karasan, O. E., Pinar, M. C.: The robust spanning tree problem with interval data. Oper. Res. Lett. 29, 31–40 (1995)
Zuluaga, L., Pena, J. F.: A conic programming approach to generalized tchebycheff inequalities. Mathematics of Operations Research 30, 369–388 (2005)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Bertsimas, D., Natarajan, K. & Teo, CP. Persistence in discrete optimization under data uncertainty. Math. Program. 108, 251–274 (2006). https://doi.org/10.1007/s10107-006-0710-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-006-0710-z