Skip to main content
Springer Nature Link
Log in

Bin packing with general cost structures

  • Full Length Paper
  • Series A
  • Published:
Mathematical Programming Submit manuscript

Abstract

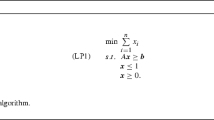
Following the work of Anily et al., we consider a variant of bin packing called bin packing with general cost structures (GCBP) and design an asymptotic fully polynomial time approximation scheme (AFPTAS) for this problem. In the classic bin packing problem, a set of one-dimensional items is to be assigned to subsets of total size at most 1, that is, to be packed into unit sized bins. However, in GCBP, the cost of a bin is not 1 as in classic bin packing, but it is a non-decreasing and concave function of the number of items packed in it, where the cost of an empty bin is zero. The construction of the AFPTAS requires novel techniques for dealing with small items, which are developed in this work. In addition, we develop a fast approximation algorithm which acts identically for all non-decreasing and concave functions, and has an asymptotic approximation ratio of 1.5 for all functions simultaneously.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Anily S., Bramel J., Simchi-Levi D.: Worst-case analysis of heuristics for the bin packing problem with general cost structures. Oper. Res. 42(2), 287–298 (1994)

    Article  MATH  Google Scholar 

  2. Baker B.S., Coffman E.G. Jr: A tight asymptotic bound for next-fit-decreasing bin-packing. SIAM J. Algebraic Discrete Methods 2(2), 147–152 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  3. Bansal N., Caprara A., Sviridenko M.: A new approximation method for set covering problems, with applications to multidimensional bin packing. SIAM J. Comput. 39(4), 1256–1278 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bansal N., Correa J.R., Kenyon C., Sviridenko M.: Bin packing in multiple dimensions: inapproximability results and approximation schemes. Math. Oper. Res. 31, 31–49 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  5. Bein W.W., Correa J.R., Han X.: A fast asymptotic approximation scheme for bin packing with rejection. Theor. Comput. Sci. 393(1–3), 14–22 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  6. Bramel J., Rhee W.T., Simchi-Levi D.: Average-case analysis of the bin packing problem with general cost structures. Nav. Res. Logistics 44(7), 673–686 (1998)

    Article  MathSciNet  Google Scholar 

  7. Caprara A., Kellerer H., Pferschy U.: Approximation schemes for ordered vector packing problems. Nav. Res. Logistics 92, 58–69 (2003)

    Article  MathSciNet  Google Scholar 

  8. Caprara A., Kellerer H., Pferschy U., Pisinger D.: Approximation algorithms for knapsack problems with cardinality constraints. Eur. J. Oper. Res. 123, 333–345 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  9. Coffman E.G., Garey M.R., Johnson D.S.: Approximation algorithms for bin packing: a survey. In: Hochbaum, D. (eds) Approximation Algorithms, PWS Publishing Company, Boston (1997)

    Google Scholar 

  10. Coffman E.G. Jr, Csirik J.: Performance guarantees for one-dimensional bin packing. In: Gonzalez, T.F. (eds) Handbook of Approximation Algorithms and Metaheuristics Chapter 32, pp. 18. Chapman and Hall/Crc, London (2007)

    Google Scholar 

  11. Csirik J., Woeginger G.J.: On-line packing and covering problems. In: Fiat, A., Woeginger, G.J. (eds) Online Algorithms: The State of the Art Chapter 7, pp. 147–177. Springer, Berlin (1998)

    Google Scholar 

  12. Dósa G., He Y.: Bin packing problems with rejection penalties and their dual problems. Inf. Comput. 204(5), 795–815 (2006)

    Article  MATH  Google Scholar 

  13. Epstein L.: Online bin packing with cardinality constraints. SIAM J. Discrete Math. 20(4), 1015–1030 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  14. Epstein L.: Bin packing with rejection revisited. Algorithmica 56(4), 505–528 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  15. Epstein, L., Levin, A.: AFPTAS results for common variants of bin packing: a new method to handle the small items. Manuscript (2007).

  16. Epstein L., Levin A.: An APTAS for generalized cost variable-sized bin packing. SIAM J. Comput. 38(1), 411–428 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  17. Fernandez de la Vega W., Lueker G.S.: Bin packing can be solved within 1 + ε in linear time. Combinatorica 1(4), 349–355 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  18. Jansen, K., van Stee, R.: On strip packing with rotations. In: Proceedings of the 37th annual ACM symposium on theory of computing (STOC2005), pp. 755–761 (2005).

  19. Johnson, D.S.: Near-optimal bin packing algorithms. PhD thesis, MIT, Cambridge, MA (1973).

  20. Johnson D.S.: Fast algorithms for bin packing. J. Comput. Syst. Sciences 8, 272–314 (1974)

    Article  MATH  Google Scholar 

  21. Johnson D.S., Demers A., Ullman J.D., Garey M.R., Graham R.L.: Worst-case performance bounds for simple one-dimensional packing algorithms. SIAM J. Comput. 3, 256–278 (1974)

    Article  MathSciNet  Google Scholar 

  22. Karmarkar, N., Karp, R.M.: An efficient approximation scheme for the one-dimensional bin-packing problem. In: Proceedings of the 23rd annual symposium on Foundations of computer science (FOCS’82), pp. 312–320 (1982).

  23. Krause K.L., Shen V.Y., Schwetman H.D.: Analysis of several task-scheduling algorithms for a model of multiprogramming computer systems. J. ACM 22(4), 522–550 (1975)

    Article  MathSciNet  MATH  Google Scholar 

  24. Lee C.C., Lee D.T.: A simple online bin packing algorithm. J. ACM 32(3), 562–572 (1985)

    Article  MATH  Google Scholar 

  25. Li C.-L., Chen Z.-L.: Bin-packing problem with concave costs of bin utilization. Nav. Res. Logistics 53(4), 298–308 (2006)

    Article  MATH  Google Scholar 

  26. Murgolo F.D.: An efficient approximation scheme for variable-sized bin packing. SIAM J. Comput. 16(1), 149–161 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  27. Seiden S.S.: On the online bin packing problem. J. ACM 49(5), 640–671 (2002)

    Article  MathSciNet  Google Scholar 

  28. Shachnai, H., Yehezkely, O.: Fast asymptotic FPTAS for packing fragmentable items with costs. In: Proceedings of the 16th international symposium on fundamentals of computation theory (FCT2007), pp. 482–493 (2007).

  29. Ullman J.D.: The Performance of a Memory Allocation Algorithm. Technical Report 100. Princeton University, Princeton NJ (1971)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Haifa, 31905, Haifa, Israel

    Leah Epstein

  2. Faculty of Industrial Engineering and Management, The Technion, Haifa, Israel

    Asaf Levin

Authors
  1. Leah Epstein
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Asaf Levin
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Asaf Levin.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Epstein, L., Levin, A. Bin packing with general cost structures. Math. Program. 132, 355–391 (2012). https://doi.org/10.1007/s10107-010-0403-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10107-010-0403-5

Mathematics Subject Classification (2000)