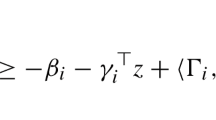Abstract
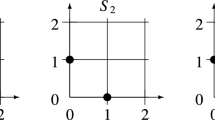
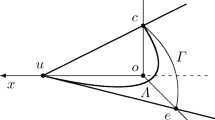
In this paper, we study properties of general closed convex sets that determine the closedness and polyhedrality of the convex hull of integer points contained in it. We first present necessary and sufficient conditions for the convex hull of integer points contained in a general convex set to be closed. This leads to useful results for special classes of convex sets such as pointed cones, strictly convex sets, and sets containing integer points in their interior. We then present a sufficient condition for the convex hull of integer points in general convex sets to be a polyhedron. This result generalizes the well-known result due to Meyer (Math Program 7:223–225, 1974). Under a simple technical assumption, we show that these sufficient conditions are also necessary for the convex hull of integer points contained in general convex sets to be a polyhedron.
Similar content being viewed by others
References
Basu A., Conforti M., Cornuéjols G., Zambelli G.: Maximal lattice-free convex sets in linear subspaces. Math. Oper. Res. 35, 704–720 (2010)
Conforti M., Cornuéjols G., Zambelli G.: Polyhedral approaches to mixed integer linear programming. In: Jünger, M., Liebling, T., Naddef, D., Nemhauser, G.L., Pulleyblank, W., Reinelt, G., Rinaldi, G., Wolsey, L.A. (eds.) 50 Years of Integer Programming 1958–2008, pp. 343–385. Springer, Berlin (2010)
Hemmecke, R.: Representations of lattice point sets: theory, algorithms, applications. Ph.D. thesis, University Magdeburg, October 2006, Habilitation thesis (2006)
Hemmecke R., Weismantel R.: Representation of sets of lattice points. SIAM J. Optim. 18, 133–137 (2007)
Hüsseinov F.: A note on the closedness of the convex hull and its applications. J. Convex Anal. 6, 387–393 (1999)
Klee V.L.: Extremal structure of convex sets. Archiv der Mathematik 8, 234–240 (1957)
Lovász, L.: Geometry of numbers and integer programming. In: Iri, M., Tanabe, K. (eds.) Mathematical Programming: Recent Developments and Applications, pp. 177–210. Kluwer, Dordrecht (1989)
Meyer R.R.: On the existance of optimal solutions of integer and mixed-integer programming problems. Math. Program. 7, 223–225 (1974)
Moussafir J.-O.: Convex hulls of integral points. J. Math. Sci. 113, 647–665 (2003)
Rockafeller G.T.: Convex Analysis. Princeton University Press, New Jersey (1970)
Schrijver A.: Theory of Linear and Integer Programming. Wiley, New York (1986)
Author information
Authors and Affiliations
Corresponding author
Additional information
This research was supported by NSF CMMI Grant 1030422.
Rights and permissions
About this article
Cite this article
Dey, S.S., Morán R., D.A. Some properties of convex hulls of integer points contained in general convex sets. Math. Program. 141, 507–526 (2013). https://doi.org/10.1007/s10107-012-0538-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-012-0538-7