Skip to main content
Springer Nature Link
Log in

Risk-averse feasible policies for large-scale multistage stochastic linear programs

  • Full Length Paper
  • Series A
  • Published:
Mathematical Programming Submit manuscript

Abstract

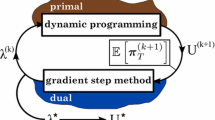
We consider risk-averse formulations of stochastic linear programs having a structure that is common in real-life applications. Specifically, the optimization problem corresponds to controlling over a certain horizon a system whose dynamics is given by a transition equation depending affinely on an interstage dependent stochastic process. We put in place a rolling-horizon time consistent policy. For each time step, a risk-averse problem with constraints that are deterministic for the current time step and uncertain for future times is solved. To each uncertain constraint corresponds both a chance and a Conditional Value-at-Risk constraint. We show that the resulting risk-averse problems are numerically tractable, being at worst conic quadratic programs. For the particular case in which uncertainty appears only on the right-hand side of the constraints, such risk-averse problems are linear programs. We show how to write dynamic programming equations for these problems and define robust recourse functions that can be approximated recursively by cutting planes. The methodology is assessed and favourably compared with Stochastic Dual Dynamic Programming on a real size water-resource planning problem.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Notes

  1. The authors specially acknowledge the good will and availability of Débora Dias Jardim Penna.

  2. We adopt the convention 1 MWMonth \(=\frac{365.25{\small {\times }}24}{12}\) MWh \(=730.5\) MWh.

  3. If \(X\) is a continuous random variable for which lower values are preferred, its Value-at-Risk of level \({\varepsilon _{\scriptstyle \mathtt{p }}}\) is given by \(\textit{VaR}_{{\varepsilon _{\scriptstyle \mathtt{p }}}}(X):=F_{X}^{-1}(1-{\varepsilon _{\scriptstyle \mathtt{p }}})\) for any \({\varepsilon _{\scriptstyle \mathtt{p }}}\in [0,1]\).

    Table 1 Central and dispersion characteristics of the total cost (R$)
    Full size table

References

  1. Artzner, P., Delbaen, F., Eber, J.-M., Heath, D.: Coherent measures of risk. Math. Finance 9, 203–228 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  2. Beaulieu, N., Abu-Dayya, A., MacLane, P.: Estimating the distribution of a sum of independent lognormal random variables. IEEE Trans. Commun. 43(12), 2869–2873 (1995)

    Article  Google Scholar 

  3. Ben-Tal, A., Goryashko, A., Guslitzer, E., Nemirovski, A.: Adjustable robust solutions of uncertain linear programs. Math. Program. 99, 351–376 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  4. Ben-Tal, A., Nemirovski, A.: Robust solutions of uncertain linear programs. Oper. Res. Lett. 25, 1–13 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  5. Ben-Tal, A., Nemirovski, A.: Selected topics in robust convex optimization. Math. Program. 112(1), 125–158 (2008). (Electronic)

    Google Scholar 

  6. Bertsimas, D., Thiele, A.: A robust optimization approach to inventory theory. Oper. Res. 54(1), 150–168 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  7. Birge, J., Louveaux, F.: Introduction to Stochastic Programming. Springer, New York (1997)

    MATH  Google Scholar 

  8. Brignol, S., Rippault, G.: Risk management applied to weekly generation scheduling. IEEE Winter Meet. Proc. 1, 465–470 (1999)

    Google Scholar 

  9. Chao, H., Poncet, A., Yuen, C.: Handling infeasibilities when applying Benders decomposition to scheduling optimization. WSEAS Trans. Power Syst. 1(7), 1209–1216 (2006)

    Google Scholar 

  10. Charnes, A., Cooper, W: Chance-constrained programming. Manag. Sci. 6, 73–79 (1959/1960)

    Google Scholar 

  11. Charnes, A., Cooper, W.: Chance constraints and normal deviates. J. Am. Stat. Assoc. 57, 134–148 (1962)

    Article  MathSciNet  MATH  Google Scholar 

  12. Charnes, A., Cooper, W.: Deterministic equivalents for optimizing and satisficing under chance constraints. Oper. Res. 11, 18–39 (1963)

    Article  MathSciNet  MATH  Google Scholar 

  13. Chen, Z.-L., Powell, W.B.: A convergent cutting-plane and partial-sampling algorithm for multistage stochastic linear programs with recourse. J. Optim. Theory Appl. 102, 497–524 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  14. Croley, T.: A manual for hydrologic time series deseasonalization and serial dependence reduction. Iowa Institute of Hydraulic Research Report, The University of Iowa, Report No. 199 (1977). http://www.iihr.uiowa.edu/products/pubvid/publications.php

  15. Dentcheva, D., Ruszczyński, A.: Optimization with stochastic dominance constraints. SIAM J. Optim. 14(2), 548–566 (2003). (Electronic)

    Article  MathSciNet  MATH  Google Scholar 

  16. Dentcheva, D., Ruszczyński, A., Shapiro, A.: Lectures on Stochastic Programming. SIAM, Philadelphia (2009)

  17. Eichhorn, A., Römisch, W.: Dynamic risk management in electricity portfolio optimization via polyhedral risk functionals. In: Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, 2008 IEEE, pp. 1–8 (2008)

  18. Eichhorn, A., Römisch, W., Wegner, I.: Polyhedral risk measures in electricity portfolio optimization. PAMM Proc. Appl. Math. Mech. 4, 7–10 (2004)

    Article  Google Scholar 

  19. Fodstad, M., Midthun, K., Romo, F., Tomasgard, A.: Optimization models for the natural gas value chain. In: Geometric Modelling, Numerical Simulation, and Optimization, pp. 521–558. SINTEF, Trondheim (2007)

  20. Guigues, V.: SDDP for some interstage dependent risk averse problems and application to hydro-thermal planning. Comput. Optim. Appl. (2011). Available at http://www.optimization-online.org/DB_HTML/2011/03/2970.html

  21. Guigues, V.: Robust production management. Optim. Eng. 10, 505–532 (2009)

    Article  MathSciNet  Google Scholar 

  22. Guigues, V., Ndiaye, P., Oustry, F., Romanet, F., Aïd, R.: Robust mid-term power generation management. Optim. 58(3), 351–371 (2009)

    Article  MATH  Google Scholar 

  23. Guigues, V., Römisch, W.: Sampling-based decomposition methods for multistage stochastic programs based on extended polyhedral risk measures. SIAM J. Optim. 22, 286–312 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  24. Guigues, V., Sagastizábal, C.: Exploiting structure of autoregressive processes in risk-averse multistage stochastic linear programs. Oper. Res. Lett. (2012). doi:10.1016/j.orl.2012.09.001

  25. Guigues, V., Sagastizábal, C.: The value of rolling horizon policies for risk-averse hydro-thermal planning. Euro. J. Oper. Res. 217, 129–140 (2012)

    Article  MATH  Google Scholar 

  26. Klein Haneveld, W.: Duality in Stochastic Linear and Dynamic Programming, Volume 274 of Lecture Notes in Economics and Mathematical Systems. Springer, Berlin (1986)

    Book  Google Scholar 

  27. Klein Haneveld, W., Vlerk, M.: Integrated chance constraints: reduced forms and algorithm. Comput. Manag. Sci. 3(4), 245–269 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  28. Krasenbrink, B., Takriti, S., Wu, L.S.-Y.: Incorporating fuel constraints and electricity spot prices into the stochastic unit commitment problem. Oper. Res. 48, 268–280 (2000)

    Article  Google Scholar 

  29. Kuhn, D., Wiesemann, W., Georghiou, A.: Primal and dual linear decision rules in stochastic and robust optimization. Math. Program. 130(1), 177–209 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  30. Maceira, M.E., Damázio, J.: The use of PAR(p) model in the stochastic dual dynamic programming optimization scheme used in the operation planning of the Brazilian hydropower system. In: VIII International Conference on Probabilistic Methods Applied to Power Systems, pp. 397–402 (2004)

  31. Maceira, M.E., Damázio, J., Costa, F., Melo, A.: Chain of models for setting the energy dispatch and spot price in the Brazilian power system. In: System Computation Conference—PSCC’02, Sevilla, Spain, pp. 1–4 (2002)

  32. Mo, B., Gjelsvik, A., Grundt, A.: Integrated risk management of hydro power scheduling and contract management. IEEE Trans. Power Syst. 16(2), 216–221 (2001)

    Article  Google Scholar 

  33. Pereira, M., Pinto, L.: Multi-stage stochastic optimization applied to energy planning. Math. Program. 52(2), 359–375 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  34. Pflug, G., Römisch, W.: Modeling, Measuring and Managing Risk. World Scientific Publishing, Hackensack (2007)

  35. Philpott, A., de Matos, V.: Dynamic sampling algorithms for multi-stage stochastic programs with risk aversion (2010). Available at http://www.optimization-online.org/DB_HTML/2010/12/2861.html

  36. Philpott, A., Guan, Z.: On the convergence of stochastic dual dynamic programming and related methods. Oper. Res. Lett. 36(4), 450–455 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  37. Prékopa, A.: Stochastic Programming, Volume 324 of Mathematics and its Applications. Kluwer, Dordrecht (1995)

    Google Scholar 

  38. Rockafellar, R.T., Uryasev, S.: Conditional value-at-risk for general loss distributions. J. Bank. Finance 26(7), 1443–1471 (2002)

    Article  Google Scholar 

  39. Ruszczyński, A., Shapiro, A. (eds.): Stochastic Programming, Volume 10 of Handbooks in Operations Research and Management Science. Elsevier, Amsterdam (2003)

  40. Ruszczyński, A., Shapiro, A.: Conditional risk mappings. Math. Oper. Res. 31(3), 544–561 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  41. Sen, S., Yu, L., Genc, T.: A stochastic programming approach to power portfolio optimization. Oper. Res. 54, 55–72 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  42. Shapiro, A.: On a time consistency concept in risk averse multi-stage stochastic programming. Oper. Res. Lett. 37, 143–147 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  43. Shapiro, A.: Analysis of stochastic dual dynamic programming method. Eur. J. Oper. Res. 209, 63–72 (2011)

    Article  MATH  Google Scholar 

  44. Wallace, S.W., Fleten, S.-E.: Stochastic Programming Models in Energy. Handbooks in Operations Research and Management Science. North Holland, Amsterdam (2003)

  45. Wu, J., Mehta, N., Zhang, J.: A flexible lognormal sum approximation method. In: Proceedings IEEE Global Telecommunications Conference GLOBECOM’05, vol. 6, pp. 3413–3417 (2005)

  46. Zanjani, M.K., Nourelfath, M., Aït-Kadi, D.: A multi-stage stochastic programming approach for production planning with uncertainty in the quality of raw materials and demand. Technical Report, CIRRELT (2009)

Download references

Acknowledgments

We would like to thank the three reviewers and the Associate Editor for beneficial comments and suggestions.

Author information

Authors and Affiliations

  1. Escola de Matemática Aplicada, Fundação Getulio Vargas, praia de Botafogo, Rio de Janeiro, Brazil

    Vincent Guigues

  2. Departamento de Engenharia Industrial, Escola Politécnica, UFRJ, Ilha do Fundão, CT, Bloco F, Rio de Janeiro, Brazil

    Vincent Guigues

  3. IMPA – Instituto de Matemática Pura e Aplicada, Estrada Dona Castorina 110, Jardim Botânico, Rio de Janeiro, RJ 22460-320, Brazil

    Vincent Guigues & Claudia Sagastizábal

Authors
  1. Vincent Guigues
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Claudia Sagastizábal
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Vincent Guigues.

Additional information

The first author’s research was supported by CNPq grant No. 382.851/07-4. The work of the second author was partially supported by grants CNPq 303840/2011-0, AFOSR FA9550-08-1-0370, NSF DMS 0707205, PRONEX-Optimization, and FAPERJ. Claudia Sagastizábal: On leave from INRIA Rocquencourt, France.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Guigues, V., Sagastizábal, C. Risk-averse feasible policies for large-scale multistage stochastic linear programs. Math. Program. 138, 167–198 (2013). https://doi.org/10.1007/s10107-012-0592-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10107-012-0592-1

Keywords

Mathematics Subject Classification