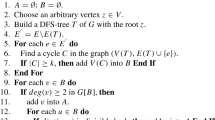Abstract
A k-matching cover of a graph \(G\) is a union of \(k\) matchings of \(G\) which covers \(V(G)\). The matching cover number of \(G\), denoted by \(mc(G)\), is the minimum number \(k\) such that \(G\) has a \(k\)-matching cover. A matching cover of \(G\) is optimal if it consists of \(mc(G)\) matchings of \(G\). In this paper, we present an algorithm for finding an optimal matching cover of a graph on \(n\) vertices in \(O(n^3)\) time (if use a faster maximum matching algorithm, the time complexity can be reduced to \(O(nm)\), where \(m=|E(G)|\)), and give an upper bound on matching cover number of graphs. In particular, for trees, a linear-time algorithm is given, and as a by-product, the matching cover number of trees is determined.



Similar content being viewed by others
References
Berge, C.: Two theorems in graph theory. Proc. Nat. Acad. Sci. USA 43, 842–844 (1957)
Bondy, J.A., Murty, U.S.R.: Graph Theory. Springer, Berlin (2008)
Cunningham, W.H.: Improved bounds for matroid partition and intersection algorithms. SIAM J. Comput. 15, 948–957 (1986)
Edmonds, J.: Paths, trees, and flowers. Can. J. Math. 17, 449–467 (1965)
Gallai, T.: Über extreme Punkt- und Kantenmengen. Ann. Univ. Sci. Bp. Eötvös Sect. Math. 2, 133–138 (1959)
Gallai, T.: Maximale Systeme unabhäangiger Kanten, Magyar Tud. Akad. Mat. Kutató Int. Közl 9, 401–413 (1964)
Goldberg, A.V., Karzanov, A.V.: Maximum skew-symmetric flows. In: Algorithms—ESA ’95 (Corfu), 155–170, Lecture Notes in Computer Science, vol. 979. Springer, Berlin (1995)
Hall, P.: On representatives of subsets. J. Lond. Math. Soc. 10, 26–30 (1935)
Korte, B., Vygen, J.: Combinatorial Optimization: Theory and Algorithms, 4th edn. Springer, Berlin (2008)
Kuhn, H.W.: The Hungarian method for the assignment problem. Naval Res. Logist. Quart. 2, 83–97 (1955)
Lawler, E.: Combinatorial Optimization: Networks and Matroids. Holt, Rinehart and Winston, New York (1976)
Lovász, L., Plummer, M.D.: Matching Theory. Elsevier Science Publishers, BV, North Holland (1986)
Micali, S., Vazirani, V.V.: An \(O(V^{1/2}E)\) algorithm for finding maximum matching in general graphs. In: Proceedings of the 21st Annual IEEE Symposium on Foundations of Computer Science, pp. 17–27 (1980)
Norman, R.Z., Rabin, M.O.: An algorithm for a minimum cover of a graph. Proc. Am. Math. Soc. 10, 315–319 (1959)
Schrijver, A.: Combinatorial Optimization: Polyhedra and Efficiency. Springer, Berlin (2003)
Author information
Authors and Affiliations
Corresponding author
Additional information
Research supported by NSFC (11101383), NSFC (11271338), and NSFC (11201432).
Rights and permissions
About this article
Cite this article
Wang, X., Song, X. & Yuan, J. On matching cover of graphs. Math. Program. 147, 499–518 (2014). https://doi.org/10.1007/s10107-013-0731-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-013-0731-3