Abstract
The extension of set functions (or capacities) in a concave fashion, namely a concavification, is an important issue in decision theory and combinatorics. It turns out that some set-functions cannot be properly extended if the domain is restricted to be bounded. This paper examines the structure of those capacities that can be extended over a bounded domain in a concave manner. We present a property termed the sandwich property that is necessary and sufficient for a capacity to be concavifiable over a bounded domain. We show that when a capacity is interpreted as the product of any sub group of workers per a unit of time, the sandwich property provides a linkage between optimality of time allocations and efficiency.
Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.Notes
\(\mathbf{1}_S\) is the indicator of \(S\): it is an \(|N|\)-dimensional vector \((\mathbf{1}_S(1),\ldots ,\mathbf{1}_S(|N|))\) such that \(\mathbf{1}_S(i)=1\) if \(i\in S\) and \(\mathbf{1}_S(i)=0\) otherwise.
We show in Sect. 5 that the results hold for non-monotonic set functions that may obtain negative values as well.
The totally balanced cover of a capacity \(v\) is a capacity \(\hat{v}\) defined by \(\hat{v}(S)=\int ^{cav} \mathbf{1}_S\ dv\), for every \(S\subseteq N\). A capacity \(v\) is totally balanced if \(v=\hat{v}\).
For a vector \(x\in \mathbb R^N\) and a coalition \(S\subseteq N\), by \(x(S)\) we mean the inner product \(\langle x, \mathbf{1}_S \rangle =\sum _{i\in S}x_i\).
References
Anscombe, F.J., Aumann, R.J.: A definition of subjective probability. Ann. Math. Stat. 34, 199–295 (1963)
Azrieli, Y., Lehrer, E.: Extendable cooperative games. J. Public Econ. Theory 9, 1069–1078 (2007)
Biswas, A.K., Parthasarathy, T., Potters, J.A.M., Voorneveld, M.: Large cores and exactness. Games Econ. Behav. 28, 112 (1999)
Bondareva, O.: The theory of the core in an n-person game (in Russian). Vestnik Leningr. Univ. 13, 141–142 (1962)
Choquet, G.: Theory of capacities. Ann. Inst. Fourier 5, 131–295 (1955)
Estévez-Fernández, A.: New characterizations for largeness of the core. Games Econ. Behav. 76, 160–180 (2012)
Lehrer, E.: A new integral for capacities. Econ. Theory 39, 157–176 (2009)
Lehrer, E., Teper, R.: Subjective Independence and Concave Expected Utility, (2014), Mimeo
Lehrer, E., Teper, R.: The concave integral over large spaces. Fuzzy Sets Syst. 16, 2130–2144 (2008)
Lovasz, L.: Submodular functions and convexity. In: Bachem, A., et al. (eds.) Mathematical Programming: The State of the Art, pp. 235–257. Springer, Berlin (1983)
Murofushi, T., Sugeno, M., Machida, M.: Non-monotonic fuzzy measures and the choquet integral. Fuzzy Sets Syst. 64, 73–86 (1994)
Schmeidler, D.: Cores of exact games. J. Math. Anal. Appl. 40, 214–225 (1972)
Schmeidler, D.: Subjective probabilities and expected utility without additivity. Econometrica 57, 571–587 (1989)
Shapley, L.S.: On balanced sets and cores. Nav. Res. Logist. Q. 14, 453–460 (1967)
Shapley, L.S.: Cores of convex games. Int. J. Game Theory 1, 11–26 (1971)
Sharkey, W.W.: Cooperative games with large cores. Int. J. Game Theory 11, 175–182 (1982)
Author information
Authors and Affiliations
Corresponding author
Additional information
Ehud Lehrer: Lehrer acknowledges the support of the Israel Science Foundation, Grant #762/045.
Appendix
Appendix
Proof of Lemma 1
Fix a capacity \(v\). The homogeneity of \(e_v\) is implied by the definition of \(\int ^{cav} \cdot dv\). Now, fix \(x\in Q\) and consider a decomposition of \(x\), \(\sum _{S\subseteq N}\alpha _S \mathbf{1}_S=x\). Letting \(i^*= \arg \max _{i\in \{1,\ldots ,n\}}\) \(x_i\), we get that \(\sum _{S\subseteq N}\alpha _S\ge \sum _{S\subseteq N, i^*\in S} \alpha _S=x_{i^*}=\max x\). Since \(e_v(x)\) is the minimum over all such decomposition, we obtain \(e_v(x)\ge \max x\). \(\square \)
Proof of Lemma 2
Let \(v\) be a capacity defined over \(N\) and \(v_S\) its sub-capacity. If \(v_S\) does not have the sandwich property, then there is an affine function \(f_S(x)=a+\sum _{i\in S}a_ix_i\) (where \(x\in [0,1]^S\)) that dominates \(v_S\), and there is no linear function dominated by \(f_S\) and that is dominating \(v_S\). Denote,
\(b\) is the maximal contribution of a coalition \(B\) in \(N{\setminus }S\) to a coalition \(A\) in \(S\). Define the following affine function over \(Q\), \(f(x)=a+\sum _{i\in S}a_ix_i+ \sum _{i\in N\setminus S}bx_i\). It is clear that \(f\) dominates \(v\). Suppose, to the contrary of the assumption that \(v\) does have the sandwich property and that there exists a linear function \(\ell (x)=\sum _{i\in N}c_ix_i\), dominated by \(f\) and is dominating \(v\). Then, \(\ell _S(x) =\sum _{i\in S}c_ix_i\) is dominated by \(f_S\) and is dominating \(v_S\). This is a contradiction.
On the other hand, if \(v\) has the sandwich property, let \(f_S\) be an affine function that dominates \(v_S\). Define \(f\) in the same way as defined above. By assumption, there is a linear function \(\ell \) that is dominating \(v\) and is dominated by \(f\). The restriction of \(\ell \) to \(S\), \(\ell _S\), is dominating \(v_S\) and is dominated by \(f_S\), implying that \(v_S\) has the sandwich property. \(\square \)
Proof of Claim 1
Suppose that the core of \(v\) is non-empty and let \(\sum \alpha _S\mathbf{1}_S\) be a decomposition of \(\mathbf{1}_N\), then by the Shapley-Bondareva theorem (Bondareva [4] and Shapley [14]), \(\sum \alpha _Sv(S)\le v(N).\) Thus, the decomposition \(\mathbf{1}_N\) of itself is optimal, implying that \(e_v(\mathbf{1}_N)\le 1\), and by Lemma 1, \(e_v(\mathbf{1}_N)= 1\).
Now suppose that \(e_v(\mathbf{1}_N)= 1\). It implies that any sharp decomposition of \(\mathbf{1}_N\), \(\sum \alpha _S\mathbf{1}_S\), satisfies \(S=N\) whenever \(\alpha _S>0\). Thus, the decomposition is in fact \(\mathbf{1}_N\) itself. \(\square \)
Proof of Claim 2
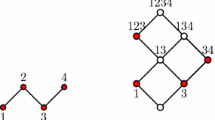
Let \(x\in Q\) and \(\sum \alpha _S\mathbf{1}_S\) be its sharp decomposition. W.l.o.g, \(\alpha _{\{12\}}\le \alpha _{\{13\}},\alpha _{\{23\}}\). Thus we can replace \(\alpha _{\{12\}}\mathbf{1}_{12}+\alpha _{\{13\}}\mathbf{1}_{13}+\alpha _{\{23\}}\mathbf{1}_{23}\) by \(2(\alpha _{\{12\}}\mathbf{1}_{123}+(\alpha _{\{13\}}-\alpha _{\{12\}})\mathbf{1}_{13}+(\alpha _{\{23\}}-\alpha _{\{12\}})\mathbf{1}_{23})\).
We conclude that one may assume that in a sharp decomposition the coefficient of \(\mathbf{1}_{12}\) is \(0.\) Furthermore, based on the total balancedness of \(v\), a similar argument would imply that no two coalitions with positive coefficients in the decomposition are disjoint. Thus, at most one singleton has a positive coefficient and the one that has a positive coefficient, if exists, is included in the other coalitions whose coefficients are positive.
We now show that there is \(i\in N\) that is a member of all coalitions whose coefficients are positive. This shows that \(e(x)= \max x\) and with the help of Theorem 1 completes the proof.
Case 1: \(\alpha _{\{1\}}>0\). Then, \(\alpha _{\{2\}}=\alpha _{\{3\}}=\alpha _{\{23\}}=0\), which means that \(1\in S\) when \(\alpha _{\{S\}}>0\). Case 2: \(\alpha _{\{2\}}>0\). Then, \(\alpha _{\{1\}}=\alpha _{\{3\}}=\alpha _{\{13\}}=0\) implying that \(2\in S\) if \(\alpha _{\{S\}}>0\). Case 3: \(\alpha _{\{3\}}>0\). Similar to the previous case. Finally, Case 4: \(\alpha _{\{i\}}=0\) for every \(i\in N\). Since \(\alpha _{\{12\}}=0\), \(3\in S\) whenever \(\alpha _{S}>0\). This completes the proof. \(\square \)
Proof of Claim 3
By Lovazc [10] (pp. 246–249), when \(v\) is convex for any \(x\in Q\), the Choquet decomposition is optimal. Thus, \(e(x)=\max x\).\(\square \)
Proof of Claim 4
Assume that any sub-capacity of \(v\) has a large core. This implies that \(v\) is totally balanced. Thus, every sub-capacity of \(v\) is totally balanced and has a large core. As such, any sub-capacity is exact (Sharkey [16]), implying that \(v\) is convex (Biswas et al. [3]). By Claim 3, \(v\) has the sandwich property.\(\square \)