The Ancestral Benders’ cutting plane algorithm with multi-term disjunctions for mixed-integer recourse decisions in stochastic programming

Abstract

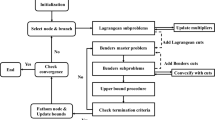
This paper focuses on solving two-stage stochastic mixed integer programs (SMIPs) with general mixed integer decision variables in both stages. We develop a decomposition algorithm in which the first-stage approximation is solved by a branch-and-bound algorithm with its nodes inheriting Benders’ cuts that are valid for their ancestor nodes. In addition, we develop two closely related convexification schemes which use multi-term disjunctive cuts to obtain approximations of the second-stage mixed-integer programs. We prove that the proposed methods are finitely convergent. One of the main advantages of our decomposition scheme is that we use a Benders-based branch-and-cut approach in which linear programming approximations are strengthened sequentially. Moreover as in many decomposition schemes, these subproblems can be solved in parallel. We also illustrate these algorithms using several variants of an SMIP example from the literature, as well as a new set of test problems, which we refer to as Stochastic Server Location and Sizing. Finally, we present our computational experience with previously known examples as well as the new collection of SMIP instances. Our experiments reveal that our algorithm is able to produce provably optimal solutions (within an hour of CPU time) even in instances for which a highly reliable commercial MIP solver is unable to provide an optimal solution within an hour of CPU time.

Appendices

Appendix 1: SSLS model formulation

To describe the model, let I be the index set for client locations and J be the index sets for possible server locations. For $i\in I$ and $j \in J$, we define the following.

Parameters

$c_j$ :

Cost of locating a server at location j.

$q_{ij}$ :

Revenue from a client at location i being served by servers at location j.

$q_{j0}$ :

Loss of revenue because of overflow at server j.

$d_{ij}$ :

Resource requirement of client i for server at location j.

r :

Upper bound on the total number of servers that can be located.

u :

Upper bound of number of server located at one location.

w :

Server capacity.

v :

Upper bound of possible number of clients.

$h^i(\omega )$ :

The number of clients at location i in scenario $\omega$

$h(\omega )$ :

The vector made of elements $h^i(\omega )$.

$p(\omega )$ :

Probability of occurrence for scenario $\omega \in \Omega$.

Decisions variables

$x_j$ :

number of servers located at site j.

$y_{ij}$ :

number of clients at location i served by servers at location j.

$y_{j0}$ :

overflow amount at server location j.

The SSLS can be formulated as follows.

$$\begin{aligned} \min \quad&\sum _{j\in J} c_j x_j - \mathsf {E}[f(x,\tilde{\omega })] \end{aligned}$$

(52a)

$$\begin{aligned} \mathbf{s.t. } \quad&\sum _{j \in J}x_j \le r, \end{aligned}$$

(52b)

$$\begin{aligned}&x_j \in \{0,1, \ldots , u\}, \quad \forall j \in J, \end{aligned}$$

(52c)

where

$$\begin{aligned} \mathsf {E}[f(x,\tilde{\omega })] = \sum _{\omega \in \Omega }p(\omega ) f(x, \omega ) \end{aligned}$$

(53)

For any x satisfying (52b, 52c) and $\omega \in \Omega$,

$$\begin{aligned} f(x,\omega ) = \min \quad&- \sum _{i \in I}\sum _{j \in J}q_{ij} y_{ij}+\sum _{j \in J}q_{j0}y_{j0} \end{aligned}$$

(54a)

$$\begin{aligned} \mathbf{s.t. } \quad&\sum _{i \in I}d_{ij}y_{ij}-y_{j0}\le w x_j, \quad \forall j \in J, \end{aligned}$$

(54b)

$$\begin{aligned}&\sum _{j \in J}y_{ij} = h^i(\omega ), \quad \forall i \in I, \end{aligned}$$

(54c)

$$\begin{aligned}&y_{ij} \in \{0,1,2,\ldots , v\}, \quad \forall i \in I, j \in J, \end{aligned}$$

(54d)

$$\begin{aligned}&y_{j0} \ge 0, \quad \forall j \in J. \end{aligned}$$

(54e)

We generated a set of SSLS instances following the method in [16]. For problem data, the server location costs $c_j$ were generated randomly from the uniform distribution in the interval [40, 80] and the client demands $d_{ij}$ were generated in the interval [0, 25]. The client-server revenue were set at one unit per unit of client demand. The overflow costs $q_{j0}$ were fixed at 1000. For scenario data, the number of clients available in each scenario $h^i(\omega )$ were generated from a binomial distribution with $p=0.5$ and v trials.

Appendix 2: Figures for examples

Fig. 2

Master problem B&B tree for $\mathbf {ABC}$ algorithm with CPT-D on Example 1.1

Fig. 3

Master problem B&B tree for $\mathbf {ABC}$ algorithm with BB-D on Example 1.1

Fig. 4

$\mathcal {G}_x (t),\mathcal {G}_z (t, \omega )$ for $\mathbf {ABC}$ algorithm with CPT-D on Example 1.1

Fig. 5

$\mathcal {G}_x (t),\mathcal {G}_z (t, \omega )$ for $\mathbf {ABC}$ algorithm with BB-D on Example 1.1

Fig. 6

Log-log plot of running time and scenarios for $\mathbf {ABC}$/BB-D for instances in Table 9