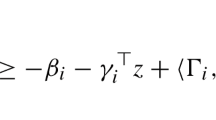Deriving convex hulls through lifting and projection

Abstract

We consider convex hull descriptions for certain sets described by inequality constraints over a hypercube and propose a lifting-and-projection technique to construct them. The general procedure obtains the convex hulls as an intersection of semi-infinite families of linear inequalities, each derived using lifting techniques that are interpreted using convexification tools. We demonstrate that differentiability and concavity of certain perturbation functions help reduce the number of inequalities needed for this characterization. Each family of inequalities yields a few linear/nonlinear constraints fully characterized in the space of the original problem variables, when the projection problems are amenable to a closed-form solution. In particular, we illustrate the complete procedure by constructing the convex hulls of the subsets of a compact hypercube defined by the constraints $x_{1}^{b_{1}} x_{2}^{b_{2}} \ge x_3$ and $x_1 x_{2}^{b_{2}} \le x_3$, where $b_1,b_2\ge 1$. As a consequence, we obtain a closed-form description of the convex hull of the bilinear equality $x_1x_2=x_3$, in the presence of variable bounds, as an intersection of a few linear and nonlinear inequalities. This explicit characterization, hitherto unknown, can improve relaxation techniques for factorable functions, which utilize this equality to relax products of functions with known relaxations.

Appendix

1.1 Proof of Lemma 5

Let $k\in \{2,3\}$ and consider the optimization problem $r_k(t,\bar{x}) =\min \{\langle \alpha , x\rangle \mid tx_2^{b_2}\le x_3, x_{k'}=\bar{x}_{k'} \text{ for } k'\ne k\}$. It follows from Lemma 1 with $q_1=b_2$, $q_2=-1$, and $h(t) = \left( \prod _{k'\ne k}\bar{x}_{k'}^{q_{k'-1}}\right) ^{-1}t^{-1}$ that $r_k(t,\bar{x})$ is concave for (i) $k=2$ because $-b_2h(t)^{b_2}$ is concave for $b_2 > 0$, and (ii) $k=3$ because $h(t)^{-1}$ is concave. Then, it follows from Remark 3 that extreme points of the epigraph of $\mathrm{conv}(\psi )(t)$ can only be at values of t where an extreme point of $[l_2,u_2]\times [l_3,u_3]$ is optimal for $\psi (t)$. By Proposition 4(i), $\alpha _2 < 0$, and $\alpha _3 > 0$, it follows that $tx_2^{b_2}\le x_3$ is tight at an optimal solution. If $(u_2,1)$ is optimal then, by Assumption (B4), $t=l_1$. If $(1,u_3)$ is optimal then, by Assumption (B6) $t=u_1$. Since these are extreme points of the region for t, the value of $\psi (t)$ at these points is needed to construct the convex envelope. Observe that (1, 1) is optimal only if $t=1$ and $\alpha _2 \ge -\alpha _3b_2$ and $(u_2,u_3)$ is optimal only if $t=u_3u_2^{-b_2}$ and $\alpha _2\le -\alpha _3b_2u_3u_2^{-1}$.

We first consider $\alpha _2 \ge -\alpha _3b_2$. Observe that, by Assumptions (B2) and (B4), $p'=\Bigl (l_1^{-b_2^{-1}},1\Bigr )$ is feasible at $t=l_1$ and, by Assumptions (B5) and (B6) $p''=(1,u_1)$ is feasible at $t=u_1$. Then, it follows that $\psi (l_1)\le \langle \alpha , p'\rangle = r_2(l_1,p')$ and $\psi (u_1) \le \langle \alpha , p''\rangle = r_3(u_1,p'')$. By Proposition 5, it follows that $(1,\psi (1))$ is an extreme point of the epigraph of $\mathrm{conv}(\psi )(t)$ only if $x_2\ge 1$ is tight at $t=u_1$ and $x_3\ge 1$ is tight at $t=l_1$ in optimal solutions to $\psi (t)$. Then, $\psi (l_1) = \langle \alpha , p'\rangle$ and $\psi (u_1) = \langle \alpha , p''\rangle$. Let $\kappa = \frac{1-l_1}{u_1-l_1}$. Then, $\langle \alpha , (1,1)\rangle < (1-\kappa )\psi (l_1) + \kappa \psi (u_1)$ if and only if $\alpha _2 > -P_1\alpha _3$. Moreover, if $x_3\ge 1$ is tight at $\psi (l_1)$, we show that $\alpha _2 > -\alpha _3b_2u_3u_2^{-1}$. If $u_3 > u_2$ this follows because $\alpha _2\ge -\alpha _3b_2 > -\alpha _3b_2u_3u_2^{-1}$. On the other hand, if $u_3\le u_2 < u_2^{b_2}$ we have shown that $(u_2,u_3)$ is optimal at $t=u_2^{-b_2}u_3 \in [l_1,1)$. However, this contradicts that $x_3\ge 1$ is tight at $\psi (l_1)$ because, if so, it would remain tight for all $t\in [l_1,1]$. It follows that $\mathrm{conv}(\psi )(t)$ is affine over $[l_1,u_1]$ for $\alpha _2 \le -P_1\alpha _3$. Otherwise, $\psi (\cdot )$ is concave over $[l_1,1]$ and $[1,u_1]$ and $\mathrm{conv}(\psi )(t) = \psi (t)$ for $t\in \{l_1,1,u_1\}$.

Now, we consider $\alpha _2 \le -\alpha _3b_2u_3u_2^{-1}$. It can be easily verified using Assumptions (B2) and (B4) that $q'=(u_2,l_1u_2^{b_2})$ is feasible at $t=l_1$ and by Assumptions (B5) and (B6) that $q''=\Bigl (u_1^{-b_2^{-1}} u_3^{b_2^{-1}},u_3\Bigr )$ is feasible at $t=u_1$. Then, it follows that $\psi (l_1)\le \langle \alpha , q'\rangle = r_3(l_1,q')$ and $\psi (u_1)\le \langle \alpha , q''\rangle = r_2(u_1,q'')$. By Proposition 5, it follows that $\left( u_2^{-b_2} u_3,\psi \bigl (u_2^{-b_2}u_3\bigr )\right)$ is an extreme point of the epigraph of $\mathrm{conv}(\psi )(t)$ only if $x_3\le u_3$ is tight at $t=u_1$ and $x_2\le u_2$ is tight at $t=l_1$. Then, $\psi (l_1) = \langle \alpha , q'\rangle$ and $\psi (u_1) = \langle \alpha , q''\rangle$. Let $\zeta = \frac{u_3u_2^{-b_2}-l_1}{u_1-l_1}$. It follows that $\langle \alpha , (u_2,u_3)\rangle < (1-\zeta )\psi (l_1) + \zeta \psi (u_1)$ if and only if $\alpha _2 < -P_2\alpha _3$. We now show that if $x_3\le u_3$ is active at $t=u_1$ then $\alpha _2 < -\alpha _3b_2$. If $u_3 > u_2$, $\alpha _2 \le -\alpha _3b_2u_2^{-1} u_3 \le -\alpha _3b_2$. On the other hand, if $u_3 \le u_2 < u_2^{b_2}$ and $\alpha _2 \ge -\alpha _3b_2$, it follows that $x_3\le u_3$ is not active at $t=1 > u_2^{-b_2} u_3$ which yields a contradiction to $x_3\le u_3$ being active at $t=u_1$. Then, it follows that $\mathrm{conv}(\psi )(t)$ is affine over $[l_1,u_1]$ for $\alpha _2 \ge -P_2\alpha _3$. Otherwise, $\psi (\cdot )$ is piecewise concave over $[l_1,u_2^{-b_2} u_3]$ and $[u_2^{-b_2} u_3,u_1]$ and $\mathrm{conv}(\psi )(t) = \psi (t)$ for $t\in \{l_1,u_2^{-b_2} u_3,u_1\}$. $\square$

1.2 Proof of Proposition 12

Proof

• Case 1: $0 < -\alpha _2 \alpha _3^{-1} \le P_1$: It follows from Lemma 5(i) that the envelope of $\psi (t)$ is piecewise affine over $[l_1,1]$ and $[1,u_1]$ (if any of these segments reduces to a point, it can be ignored in the foregoing discussion.) We can therefore develop at most two inequalities for each such $(\alpha _2,\alpha _3)$. Since $\psi (l_1)=\psi ^{d}(l_1)$, $\psi (1)=\alpha _2 + \alpha _3$ and $\psi (u_1)=\psi ^{e}(u_1)$, see Lemma 6 for the values of $\psi (\cdot )$ at $l_1$ or $u_1$, it follows from (3) that $(\alpha _1,\delta )$ are linear functions of $(\alpha _2,\alpha _3)$. As a result, it is sufficient to consider the situation where $-\alpha _2 \alpha _3^{-1}=P_1$. In this case, the convex envelope of $\psi (t)$ reduces to an affine function over $[l_1,u_1]$. We thus obtain (50).

• Case 2: $P_1< -\alpha _2 \alpha _3^{-1} < P_2$: It follows from Lemma 5(ii) that the convex envelope of $\psi (t)$ is affine over $[l_1,u_1]$. It is therefore sufficient to consider the values of $\psi (t)$ at $t=l_1$ and $t=u_1$.

• Case 2.1: $P_1< -\alpha _2 \alpha _3^{-1} < b_2 l_1^{b_{2}^{-1}}$: As in Case 1, it follows from (3) that lifting coefficients $(\alpha _1,\delta )$ are linear in $\alpha _2$ and $\alpha _3$. Since the interval of interest for $-\alpha _2 \alpha _3^{-1}$ is open, we conclude that these inequalities are not needed in the description of $\mathrm{conv}(S^{\le })$.

• Case 2.2: $b_2 l_1^{b_{2}^{-1}}\le -\alpha _2 \alpha _3^{-1} < \min \{b_2,b_2 l_1 u_2^{b_2-1}\}$: Here, $b_2>1$. Since $\psi (l_1)=\psi ^{c}(l_1)$ and $\psi (u_1)=\psi ^{e}(u_1)$, (4) reduces to (54).

• Case 2.3: $\min \{b_2,b_2 l_1 u_2^{b_2-1}\} \le -\alpha _2 \alpha _3^{-1} \le \max \{b_2 u_1,b_2 \frac{u_3}{u_2}\}$: There are two subcases.

  • Case 2.3.1: $b_2<b_2 l_1 u_2^{b_2-1}$: In order for this case to occur, we must have that $b_2>1$. It follows that $\psi ^{c}(t)$ is well-defined. Assume first that $b_2 u_1< b_2 l_1 u_2^{b_2-1}$. When $-\alpha _2 \alpha _3^{-1} \in [b_2,b_2 u_1]$, we obtain (54) similarly to Case 2.2. When $-\alpha _2 \alpha _3^{-1} \in (b_2 u_1,b_2 l_1 u_2^{b_2-1})$, then $\psi (l_1)=\psi ^{c}(l_1)$ and $\psi (u_1)=\psi ^{c}(u_1)$. Therefore, (4) reduces to (55). When $-\alpha _2 \alpha _3^{-1} \in [b_2 l_1 u_2^{b_2-1},b_2 \frac{u_3}{u_2}]$, then $\psi (l_1)=\psi ^{a}(l_1)$ and $\psi (u_1)=\psi ^{c}(u_1)$. Applying (4), we obtain (56). Assume second that $b_2 l_1 u_2^{b_2-1}\le b_2 u_1$. When $-\alpha _2 \alpha _3^{-1} \in [b_2,b_2 l_1 u_2^{b_2-1}]$, we obtain (54). When $-\alpha _2 \alpha _3^{-1} \in (b_2 l_1 u_2^{b_2-1}, \max \{b_2 \frac{u_3}{u_2},b_2 u_1\}]$, there are two cases. If $b_2 \frac{u_3}{u_2}\le b_2 u_1$, it follows from (3) that lifting coefficients $(\alpha _1,\delta )$ are linear in $\alpha _2$ and $\alpha _3$ when $-\alpha _2 \alpha _3^{-1} \in (b_2 l_1 u_2^{b_2-1},b_2 u_1]$ since $\psi (l_1)=\psi ^{a}(l_1)$ and $\psi (u_1)=\psi ^{e}(u_1)$. Since the interval of interest for $-\alpha _2 \alpha _3^{-1}$ is semi-open, we conclude that the only inequality that is required in the description of $\mathrm{conv}(S^{\le })$ occurs when $-\alpha _2 \alpha _3^{-1}=b_2 u_1$. We obtain (52). If $b_2 \frac{u_3}{u_2}> b_2 u_1$, it follows similarly that lifting coefficients $(\alpha _1,\delta )$ are linear in $\alpha _2$ and $\alpha _3$ when $-\alpha _2 \alpha _3^{-1} \in (b_2 l_1 u_2^{b_2-1},b_2 u_1)$. Since the interval of interest for $-\alpha _2 \alpha _3^{-1}$ is open, we conclude that none of these inequalities are required in the description of $\mathrm{conv}(S^{\le })$. When $-\alpha _2 \alpha _3^{-1} \in [b_2 u_1, b_2 \frac{u_3}{u_2}]$, we obtain (56) since $\psi (l_1)=\psi ^{a}(l_1)$ and $\psi (u_1)=\psi ^{c}(u_1)$.

  • Case 2.3.2: $b_2\ge b_2 l_1 u_2^{b_2-1}$: Assume first that $b_2 u_1\ge b_2 \frac{u_3}{u_2}$. When $-\alpha _2 \alpha _3^{-1} \in [b_2 l_1 u_2^{b_2-1},b_2 u_1]$, it is easily verified from (3) that lifting coefficients $(\alpha _1,\delta )$ are linear in $\alpha _2$ and $\alpha _3$ since $\psi (l_1)=\psi ^{a}(l_1)$, $\psi (u_1)=\psi ^{e}(u_1)$. It therefore suffices to consider the case where $-\alpha _2 \alpha _3^{-1}=b_2 l_1 u_2^{b_2-1}$ and $-\alpha _2 \alpha _3^{-1}=b_2 u_1$. We obtain (51) and (52) respectively. Assume second that $b_2 u_1<b_2 \frac{u_3}{u_2}$. For $-\alpha _2 \alpha _3^{-1} \in [b_2 l_1 u_2^{b_2-1},b_2 u_1)$, the derivation in the previous line shows that it is sufficient to consider the case where $-\alpha _2 \alpha _3^{-1}=b_2 l_1 u_2^{b_2-1}$, yielding (51). For $-\alpha _2 \alpha _3^{-1} \in [b_2 u_1,b_2 \frac{u_3}{u_2}]$, $\psi (l_1)=\psi ^{a}(l_1)$ and $\psi (u_1)=\psi ^{c}(u_1)$, yielding (56).

• Case 2.4: $\max \{b_2 u_1, b_2 \frac{u_3}{u_2}\} < -\alpha _2 \alpha _3^{-1} \le b_2 u_1^{b_{2}^{-1}} u_3^{1-b_{2}^{-1}}$: This case only occurs when $b_2>1$ and is similar to Case 2.2. Since $\psi (l_1)=\psi ^{a}(l_1)$ and $\psi (u_1)=\psi ^{c}(u_1)$, (4) reduces to (56).

• Case 2.5: $b_2 u_1^{b_{2}^{-1}} u_3^{1-b_{2}^{-1}}< -\alpha _2 \alpha _3^{-1} < P_2$: It follows from (3) that $(\alpha _1,\delta )$ are linear in $\alpha _2$ and $\alpha _3$ since $\psi (l_1)=\psi ^{a}(l_1)$ and $\psi (u_1)=\psi ^{b}(u_1)$. Since the interval of interest for $-\alpha _2 \alpha _3^{-1}$ is open, we conclude that these inequalities are not needed in the description of $\mathrm{conv}(S^{\le })$.

• Case 3: $P_2\le -\alpha _2 \alpha _3^{-1}$: It follows from Lemma 5(iii) that the envelope of $\psi (t)$ is piecewise affine over $[l_1,u_{2}^{-b_{2}} u_3]$ and $[u_{2}^{-b_{2}} u_3,u_1]$ (if any of these segments reduces to a point, it can be ignored in the foregoing discussion.) We can therefore develop at most two inequalities for each such $(\alpha _2,\alpha _3)$. Since $\psi (l_1)=\psi ^{a}(l_1)$, $\psi (u_{2}^{-b_{2}} u_3)=\alpha _2u_2 + \alpha _3u_3$ and $\psi (u_1)=\psi ^{b}(u_1)$, it follows from (3) that $(\alpha _1,\delta )$ is linear in $(\alpha _2,\alpha _3)$ in each case. It is therefore sufficient to consider the case where $-\alpha _2 \alpha _3^{-1}=P_2$. (Observe that the inequality obtained as $-\alpha _2 \alpha _3^{-1}\rightarrow +\infty$ was already obtained when considering the case $\alpha _3=0$). In this case, the convex envelope of $\psi (t)$ over $[l_1,u_1]$ reduces to an affine function. We obtain (53).

$\square$