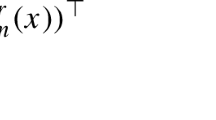Skip to main content
Springer Nature Link
Log in

Outer approximation for integer nonlinear programs via decision diagrams

  • Full Length Paper
  • Series A
  • Published:
Mathematical Programming Submit manuscript

Abstract

As an alternative to traditional integer programming (IP), decision diagrams (DDs) provide a new solution technology for discrete problems exploiting their combinatorial structure and dynamic programming representation. While the literature mainly focuses on the competitive aspects of DDs as a stand-alone solver, we investigate their complementary role by introducing IP techniques that can be derived from DDs and used in conjunction with IP to enhance the overall performance. This perspective allows for studying problems with more general structure than those typically modeled via recursive formulations. In particular, we develop linear programming and subgradient-type methods to generate valid inequalities for the convex hull of the feasible region described by DDs. For convex IPs, these cutting planes dominate the so-called linearized cuts used in the outer approximation framework. These cutting planes can also be derived for nonconvex IPs, which leads to a generalization of the outer approximation framework. Computational experiments show significant optimality gap improvement for integer nonlinear programs over the traditional cutting plane methods employed in the state-of-the-art solvers.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Andersen, H.R., Hadz̆ić, T., Hooker, J.N., Tiedemann, P.: A constraint store based on multivalued decision diagrams. In: Bessiére, C. (ed.) Principles and Practice of Constraint Programming-CP 2007, vol. 4741, pp. 118–132. Springer, New York (2007)

    Chapter  Google Scholar 

  2. Balas, E.: Disjunctive programming. Ann. Discrete Math. 5, 3–51 (1979)

    Article  MathSciNet  Google Scholar 

  3. Balas, E.: Disjunctive programming and a hierarchy of relaxations for discrete optimization problems. SIAM J. Discrete Math. 6, 466–486 (1985)

    Article  MathSciNet  Google Scholar 

  4. Behle, M.: Binary decision diagrams and integer programming. PhD thesis, Max Planck Institute for Computer Science (2007)

  5. Belotti, P., Lee, J., Liberti, L., Margot, F., Wächter, A.: Branching and bounds tightening techniques for non-convex minlp. Optim. Methods Softw. 24, 597–634 (2009)

    Article  MathSciNet  Google Scholar 

  6. Belotti, P., Kirches, C., Leyffer, S., Linderoth, J., Luedtke, J., Mahajan, A.: Mixed-integer nonlinear optimization. Acta Numberica 22, 1–131 (2013)

    Article  MathSciNet  Google Scholar 

  7. Bergman, D., Cire, A.A.: Discrete nonlinear optimization by state-space decompositions. Manag. Sci. 64, 4700–4720 (2018)

  8. Bergman, D., Cire, A.A., van Hoeve, W.J., Hooker, J.: Optimization bounds from binary decision diagrams. INFORMS J. Comput. 26, 253–268 (2013)

    Article  MathSciNet  Google Scholar 

  9. Bergman, D., Cire, A.A., van Hoeve, W.J., Hooker, J.: Decision Diagrams for Optimization. Springer, New York (2016a)

    Book  Google Scholar 

  10. Bergman, D., Cire, A.A., van Hoeve, W.J., Hooker, J.: Discrete optimization with decision diagrams. INFORMS J. Comput. 28, 47–66 (2016b)

    Article  MathSciNet  Google Scholar 

  11. Bertsekas, D.P.: Nonlinear Programming. Athena Scientific, Belmont (1999)

    MATH  Google Scholar 

  12. Bixby, R.E.: A brief history of linear and mixed integer programming computation. Documenta Mathematica, 107–121 (2012)

  13. Bonami, P., Kilinç, M., Linderoth, J.: Algorithms and software for convex mixed integer nonlinear programs. In: Lee, J., Leyffer, S. (eds.) Mixed Integer Nonlinear Programming. The IMA Volumes in Mathematics and its Applications, vol. 154. Springer, New York (2012a)

    MATH  Google Scholar 

  14. Bonami, P., Linderoth, J.T., Lodi, A.: Disjunctive cuts for mixed integer nonlinear programming problems. Technical Report (2012b)

  15. Boukouvalaa, F., Misener, R., Floudas, C.A.: Global optimization advances in mixed-integer nonlinear programming, MINLP, and constrained derivative-free optimization, CDFO. Eur. J. Oper. Res. 252, 701–727 (2016)

    Article  MathSciNet  Google Scholar 

  16. Burer, S., Letchford, A.N.: Non-convex mixed-integer nonlinear programming: a survey. Surv. Oper. Res. Manag. Sci. 17, 97–106 (2012)

    MathSciNet  Google Scholar 

  17. Ciré, A.A., van Hoeve, W.J.: Multivalued decision diagrams for sequencing problems. Oper. Res. 61, 1411–1428 (2013)

    Article  MathSciNet  Google Scholar 

  18. Conforti, M., Cornuéjols, G., Zambelli, G.: Integer Programming. Springer, New York (2014)

    MATH  Google Scholar 

  19. Dean, J.: Pricing policies for new products. Harv. Bus. Rev. 54, 141–153 (1976)

    Google Scholar 

  20. Dunning, I., Huchette, J., Lubin, M.: Jump: a modeling language for mathematical optimization. SIAM Rev. 59(2), 295–320 (2017). https://doi.org/10.1137/15M1020575

    Article  MathSciNet  MATH  Google Scholar 

  21. Duran, M.A., Grossmann, I.: An outer-approximation algorithm for a class of mixed-integer nonlinear programs. Math. Program. 36, 307–339 (1986)

    Article  MathSciNet  Google Scholar 

  22. Eppstein, D.: Quasiconvex programming. In: Goodman, J.E., Pach, J., Welzl, E. (eds.) Combinatorial and Computational Geometry, vol. 52, pp. 287–331. MSRI Publications, Cambridge (2005)

    Google Scholar 

  23. Garey, M.R., Johnson, D.S.: Computers and Intractability: A Guide to the Theory of NP-Completeness. W. H. Freeman and Company, New York (1979)

    MATH  Google Scholar 

  24. Geoffrion, A.: Generalized benders decomposition. J. Optim. Theory Appl. 10, 237–260 (1985)

    Article  MathSciNet  Google Scholar 

  25. Hadz̆ić, T., Hooker, J.N.: Discrete global optimization with binary decision diagrams. In: Workshop on Global Optimization: Integrating Convexity, Optimization, Logic Programming, and Computational Algebraic Geormetry (GICOLAG) (2006)

  26. Hemmecke, R., Köppe, M., Lee, J., Weismantel, R.: Nonlinear integer programming. In: Jünger, M., Liebling, T.M., Naddef, D., Nemhauser, G.L., Pulleyblank, W.R., Reinelt, G., Rinaldi, G., Wolsey, L.A. (eds.) 50 Years of Integer Programming 1958–2008, pp. 561–618. Springer, New York (2009)

    MATH  Google Scholar 

  27. Holdershaw, J., Gendall, P., Garland, R.: The widespread use of odd pricing in the retail sector. Mark. Bull. 8, 53–58 (1997)

    Google Scholar 

  28. Kilinc, M., Linderoth, J., Luedtke, J.: Lift-and-project cuts for convex mixed integer nonlinear programs. Math. Program. Comput. 9, 499–526 (2017)

    Article  MathSciNet  Google Scholar 

  29. Kronqvist, J., Lundell, A., Westerlund, T.: The extended supporting hyperplane algorithm for convex mixed-integer nonlinear programming. J. Glob. Optim. 64, 249–272 (2016)

    Article  MathSciNet  Google Scholar 

  30. Kronqvist, J., Bernal, D., Lundell, A., Grossmann, I.: A review and comparison of solvers for convex MINLP. Optim. Eng. 20, 397–455 (2017)

    Article  MathSciNet  Google Scholar 

  31. Lee, C.Y.: Representation of switching circuits by binary-decision programs. Bell Syst. Tech. J. 38, 985–999 (1959)

    Article  MathSciNet  Google Scholar 

  32. Lozano, L., Smith, J.C.: A binary decision diagram based algorithm for solving a class of binary two-stage stochastic programs. Mathematical Programming pp 1–24 (2018)

  33. Nagle, T., Hogan, J., Zale, J.: The Strategy and Tactics of Pricing: A Guide to Growing More Profitably. Prentice Hall, London (2011)

    Google Scholar 

  34. Quesada, I., Grossmann, I.E.: An LP/NLP based branch-and-bound algorithm for convex MINLP optimization problems. Comput. Chem. Eng. 16, 937–947 (1992)

    Article  Google Scholar 

  35. St-Aubin, R., Hoey, J., Boutilier, C.: Approximation policy construction using decision diagrams. In: Proceedings of Conference on Neural Information Processing Systems, Nantes, France, pp. 1089–1095 (2000)

  36. Tawarmalani, M., Sahinidis, N.V.: Convexification and Global Optimization in Continuous and Mixed-Integer Nonlinear Programming: Theory, Algorithms, Software, and Applications. Kluwer Academic Publishers, Dordrecht (2002)

    Book  Google Scholar 

  37. Tjandraatmadja, C., van Hoeve, W.J.: Target cuts from relaxed decision diagrams. INFORMS J. Comput. 31, 285–301 (2019)

    Article  MathSciNet  Google Scholar 

  38. Vigerske, S.: A library of mixed-integer and continuous nonlinear programming instances. https://minlplib.org (2019)

  39. Wegener, I.: Branching Programs and Binary Decision Diagrams: Theory and Applications. Society for Industrial and Applied Mathematics, Philadelphia (2000)

    Book  Google Scholar 

  40. Westerlund, T., Pettersson, F.: A cutting plane method for solving convex MINLP problems. Comput. Chem. Eng. 19, s131–s136 (1995)

    Article  Google Scholar 

Download references

Acknowledgements

We thank Nick Sahinidis and Michael Bussieck for providing GAMS license for our experiments. We also thank the anonymous referees and the Associate Editor for their helpful comments that contributed to improving the paper.

Author information

Authors and Affiliations

  1. Industrial and Manufacturing Systems Engineering, Iowa State University, Ames, IA, USA

    Danial Davarnia

  2. Tepper School of Business, Carnegie Mellon University, Pittsburgh, PA, USA

    Willem-Jan van Hoeve

Authors
  1. Danial Davarnia
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Willem-Jan van Hoeve
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Danial Davarnia.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material 1 (pdf 3739 KB)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Davarnia, D., van Hoeve, WJ. Outer approximation for integer nonlinear programs via decision diagrams. Math. Program. 187, 111–150 (2021). https://doi.org/10.1007/s10107-020-01475-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10107-020-01475-4

Keywords

Mathematics Subject Classification