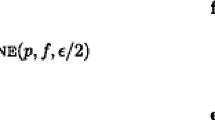Convex hull results for generalizations of the constant capacity single node flow set

Abstract

For single node flow sets with fixed costs and constant capacities on the inflow and outflow arcs, a family of constant capacity flow covers are known to provide the convex hull in different special cases and are conjectured to provide it in the general case. Here we study more general mixed integer sets for which such single node flow cover inequalities suffice to give the convex hull. In particular we consider the case of a path in which each node has one (or several) incoming and outgoing arcs with constant capacities and fixed costs. This can be seen as a lot-sizing set with production and sales decisions driven by costs and prices and by the lower and upper bounds on stocks instead of being driven by demands as in the standard lot-sizing model. The approach we take is classical: we characterize the extreme points, derive tight extended formulations and project out the additional variables. Specifically we show that Fourier–Motzkin elimination, though far from elegant, can be used to carry out the non-trivial projections. The validity of the conjecture for the single node flow set follows from our results.

Appendices

Appendix 1: Proof of Theorem 3

The proof is by induction. The result holds for $k=n$. We show that if it holds for k, then it holds for $k-1$.

For ease of presentation, we introduce $\pi _u=\min \{x_u, (c-\lambda )z_u\}$ for $u\in [1,n]$.

1.1 Elimination of $\alpha ^2_k$ and $\sigma ^2_k$

The first step is to use the equations (73) and (74) for $t=k$ to eliminate $\alpha ^2_k$ and $\sigma ^2_k$ by substitution.

Inequality (77) for $t=k$ becomes

$$\begin{aligned} s_k \le (c-\lambda )(\sigma ^1_{k-1}+\sigma ^2_{k-1})+x_k-\lambda \alpha ^1_k + \lambda \sigma ^1_k. \end{aligned}$$

(108)

Inequality (78) for $t=k$ becomes

$$\begin{aligned} x_k \le (c-\lambda )z_k+\lambda \alpha ^1_k. \end{aligned}$$

(109)

Inequality (79) for $t=k$ becomes

$$\begin{aligned} x_k-c\alpha ^1_k \le s_k-c\sigma ^1_k. \end{aligned}$$

(110)

Inequality (81) for $t=k$ becomes

$$\begin{aligned} s_k \le c\sigma ^1_k+(c-\lambda ). \end{aligned}$$

(111)

Inequality (82) for $t=k$ becomes

$$\begin{aligned} x_k \ge c\alpha ^1_k. \end{aligned}$$

(112)

Inequalities (72) for $t \in [k+1,n]$ become

$$\begin{aligned} s_t \le \lambda \left\lfloor \frac{b_t}{c} \right\rfloor +\pi _{k+1,t}-\lambda \sigma ^1_k+s_k. \end{aligned}$$

(113)

1.2 Elimination of $\alpha ^1_k$

Now we use Fourier–Motzkin to eliminate $\alpha ^1_k$. We have to combine the inequalities (108) and (112) with the inequalities (76), (83), (109) and (110).

Inequality (76) with (108) gives

$$\begin{aligned} s_k \le x_k+s_{k-1}. \end{aligned}$$

Inequality (76) with (112) gives

$$\begin{aligned} x_k \ge c(\sigma ^1_k-\sigma ^1_{k-1}). \end{aligned}$$

(114)

Inequality (83) with (112) gives

$$\begin{aligned} x_k \ge 0. \end{aligned}$$

Inequality (83) with (108) gives

$$\begin{aligned} s_k \le (c-\lambda )(\sigma ^1_{k-1}+\sigma ^2_{k-1})+x_k+ \lambda \sigma ^1_k. \end{aligned}$$

(115)

Inequality (109) with (108) gives

$$\begin{aligned} s_k \le (c-\lambda )z_k+(c-\lambda )(\sigma ^1_{k-1}+\sigma ^2_{k-1})+\lambda \sigma ^1_k. \end{aligned}$$

(116)

These inequalities (115) and (116) together give

$$\begin{aligned} s_k \le \pi _k+(c-\lambda )(\sigma ^1_{k-1}+\sigma ^2_{k-1})+\lambda \sigma ^1_k. \end{aligned}$$

(117)

Inequality (109) with (112) gives

$$\begin{aligned} x_k \le cz_k. \end{aligned}$$

Inequality (110) with (108) gives

$$\begin{aligned} s_k \le x_k +c(\sigma ^1_{k-1}+\sigma ^2_{k-1}). \end{aligned}$$

(118)

Inequality (110) with (112) gives

$$\begin{aligned} s_k \ge c \sigma ^1_k. \end{aligned}$$

(119)

Note that inequality (118) is redundant as it is dominated by (114).

1.3 Elimination of $\sigma ^1_k$

$\sigma ^1_k$ occurs in the inequalities (80), (113), (114), (119) and with the opposite sign in (82), (111), (117). We treat inequalities (80) and (113) together as (80) is the same as (113) for $t=k$.

Combining (82) with (119) gives

$$\begin{aligned} s_k \ge 0. \end{aligned}$$

Combining (111) with (113) for $t\in [k,n]$ gives

$$\begin{aligned} cs_t-(c-\lambda )s_k \le \lambda b_t +c\pi _{k+1,t}. \end{aligned}$$

For $t=k$, we obtain

$$\begin{aligned} s_k \le b_k. \end{aligned}$$

For $t\in [k+1,n]$, these inequalities are redundant. To see this, we take inequality $s_u -s_{u-1} \le x_u$ for $[u \in k+1,t]$ with weight $(c-\lambda )$ and $s_t \le b_t$ with weight $\lambda$. We obtain $cs_t-(c-\lambda )s_k \le \lambda b_t +(c-\lambda )x_{k+1,t}$. Now $(c-\lambda )x_u \le cx_u$ and as $x_u \le cz_u$, $(c-\lambda )x_u \le c(c-\lambda )z_u$. Thus $(c-\lambda )x_u \le c \pi _u$ for $u\in [k+1,t]$ and the inequality is dominated. Combining (117) with (113) for $t\in [k,n]$ gives

$$\begin{aligned} s_t \le \lambda \left\lfloor \frac{b_t}{c} \right\rfloor +\pi _{kt}+(c-\lambda )(\sigma ^1_{k-1}+\sigma ^2_{k-1}) \;\;\; t\in [k,n]. \end{aligned}$$

Note that these are inequalities (72) of $R^{k-1}{\setminus } R^k$.

Combining (82) with (113) for $t\in [k,n]$ gives

$$\begin{aligned} s_t-s_k \le \left\lfloor \frac{b_t}{c} \right\rfloor \lambda +\pi _{k+1,t}. \end{aligned}$$

The inequality is redundant for $t=k$. For $t\in [k+1, n]$, we obtain the inequalities (71) for $j=k$ of $R^{k-1}{\setminus } R^k$.

Note that we have obtained all the inequalities describing $R^{k-1}$.

It now suffices to show that the remaining inequalities are redundant for $Q^{k-1} \cap R^{k-1}$.

Combining (82) with (80) and (114) give $\left\lfloor \frac{b_k}{c} \right\rfloor \ge 0$ and $x_k +c\sigma ^1_{k-1} \ge 0$, respectively. These are both redundant.

Combining (111) with (119) gives $c-\lambda \ge 0$, which is redundant.

Combining (111) with (114) gives

$$\begin{aligned} s_k \le x_k+c\sigma ^1_{k-1}+(c-\lambda ). \end{aligned}$$

Combining (117) with (119) gives

$$\begin{aligned} (c-\lambda )s_k \le c\pi _k+c(c-\lambda )(\sigma ^1_{k-1}+\sigma ^2_{k-1}). \end{aligned}$$

Combining (117) with (114) gives

$$\begin{aligned} cs_k \le (c+\lambda )\pi _k+cs_{k-1}. \end{aligned}$$

The last three inequalities are all dominated using (114), $s_k \le x_k+s_{k-1}$ and (118), $x_k \le cz_k$ together with $\pi _k=\min \{x_k, (c-\lambda )z_k\}$ and $s_{k-1}=c\sigma ^1_{k-1}+(c-\lambda )\sigma ^2_{k-1}$.

Now the result follows by induction as $R^0 \cap Q^0$ is as claimed in the Theorem. $\square$

Appendix 2: Proof of Theorem 4

Suppose that after the elimination of variables for $t \in [k+1,n]$, we obtain $P_k\cap R_k$ plus inequalities (106) and (107) for $t\in [k+1,n]$. We will show that after eliminating $\mu ^0_k$, $\mu ^1_k$ and $\mu ^2_k$, we obtain $P_{k-1}\cap R_{k-1}$ plus inequalities (106) and (107) for $t\in [k,n]$.

1.1 Elimination of $\mu ^0_k$

The first step is the elimination of $\mu ^0_k$ by substitution. The inequalities $\mu ^0_k \le \mu ^0_{k-1}$, $\mu ^0_k \le \mu ^1_k$, $\mu ^0_k-\zeta _k \le \left\lfloor \frac{b}{c} \right\rfloor$ and $\mu ^2_k-\mu ^0_k \le 1$ give

$$\begin{aligned}&\sigma _k \le (c-\beta )\mu ^0_{k-1 } +(\beta -\alpha )\mu ^1_k+\alpha \mu ^2_k, \end{aligned}$$

(120)

$$\begin{aligned}&\sigma _k \le (c-\alpha )\mu ^1_k +\alpha \mu ^2_k, \end{aligned}$$

(121)

$$\begin{aligned}&\sigma _k-(c-\beta )\zeta _k \le (c-\beta ) \left\lfloor \frac{b}{c} \right\rfloor +(\beta -\alpha )\mu ^1_k+\alpha \mu ^2_k, \end{aligned}$$

(122)

$$\begin{aligned}&-\sigma _k+(\beta -\alpha )\mu ^1_k+(c-\beta +\alpha )\mu ^2_k \le (c-\beta ), \end{aligned}$$

(123)

respectively.

1.2 Elimination of $\mu ^1_k$

Now we eliminate $\mu ^1_k$ using Fourier–Motzkin elimination. Overall, after eliminating $\mu ^0_k$, we are left with $P_{k-1}\cap R_k$ plus (97), (98), (101), (106), (107), (120), (121), (122) and (123).

The constraints involving $\mu ^1_k$ are all these inequalities except (97) for $i=2$ and (101).

As (122) is the same as (106) for $t=k$, we treat them together.

The resulting inequalities are: (97) and (106) for $t\in [k,n]$ give

$$\begin{aligned} (\beta -\alpha )\mu ^1_{k-1} \ge \sigma _t-(c-\beta ) \left( \zeta _t+\left\lfloor \frac{b}{c} \right\rfloor \right) -\alpha \mu ^2_k \ \ t \in [{k},n]. \end{aligned}$$

(124)

(97) and (107) for $t\in [k+1,n]$ give

$$\begin{aligned} (\beta -\alpha )\mu ^1_{k-1} \ge \sigma _t-(c-\beta +\alpha )\left( \zeta _t+\left\lfloor \frac{b}{c} \right\rfloor \right) -\alpha \ \ t \in [k+1,n]. \end{aligned}$$

(125)

(97) and (120) give

$$\begin{aligned} (\beta -\alpha )\mu ^1_{k-1} \ge \sigma _k-\alpha \mu ^2_k -(c-\beta )\mu ^0_{k-1}. \end{aligned}$$

(126)

(97) and (121) give $(c-\alpha )\mu ^1_{k-1} \ge \sigma _k-\alpha \mu ^2_k$. This is redundant since adding (126) and $(c-\beta )$ times $\mu ^1_{k-1} \ge \mu ^0_{k-1}$ gives this inequality.

(98) and (106) for $t\in [k,n]$ give

$$\begin{aligned} \beta \mu ^2_k \ge \sigma _t-(c-\beta )\left( \left\lfloor \frac{b}{c} \right\rfloor +\zeta _t \right) \ \ t \in [{k},n]. \end{aligned}$$

(127)

(98) and (107) give $(\beta -\alpha )\mu ^2_{k} \ge \sigma _t-(c-\beta +\alpha )(\zeta _t+ \left\lfloor \frac{b}{c} \right\rfloor ) -\alpha \ \ t \in [k+1,n]$. This is redundant as it can be obtained by taking $b \ge \sigma _t-c\zeta _t$ with weight $\frac{\alpha }{\beta }$ and (127) for t with weight $\frac{\beta -\alpha }{\beta }$.

(98) and (120) give

$$\begin{aligned} \beta \mu ^2_{k} \ge \sigma _k -(c-\beta )\mu ^0_{k-1}. \end{aligned}$$

(128)

(98) and (121) give

$$\begin{aligned} c\mu ^2_{k} \ge \sigma _k. \end{aligned}$$

(129)

(123) and (106) for $t\in [k,n]$ give

$$\begin{aligned} \sigma _k-(c-\beta )\mu ^2_k+(c-\beta ) \left( \left\lfloor \frac{b}{c} \right\rfloor +1+\zeta _t\right) \ge \sigma _t \ \ t \in [{k},n]. \end{aligned}$$

For $t\in [k+1,n]$, the inequality is redundant since adding $\frac{c-\beta }{c-\beta +\alpha }$ times (131) (obtained from (123) and (107) below) and $\frac{\alpha }{c-\beta +\alpha }$ times $\sigma _k\ge \sigma _t$ gives this inequality. For $t=k$, we obtain

$$\begin{aligned} \mu ^2_k - \zeta _k\le 1+\left\lfloor \frac{b}{c} \right\rfloor . \end{aligned}$$

(130)

(123) and (107) give

$$\begin{aligned} \sigma _k-(c-\beta +\alpha )\mu ^2_k+(c-\beta +\alpha )\left( \left\lfloor \frac{b}{c} \right\rfloor +1+\zeta _t \right) \ge \sigma _t \ \ t \in [k+1,n]. \end{aligned}$$

(131)

(123) and (120) give $\mu ^2_k \le \mu ^0_{k-1} +1$. This is redundant since $\mu ^2_k \le \mu ^2_{k-1} \le \mu ^0_{k-1}+1$.

(123) and (121) give

$$\begin{aligned} -\sigma _k+c\mu ^2_k \le c-\alpha . \end{aligned}$$

(132)

The resulting formulation is $P_{k-1}\cap R_k$ plus inequalities

$$\begin{aligned} (125)&\sigma _t-(c-\beta +\alpha )\zeta _t-(\beta -\alpha )\mu ^1_{k-1} \le (c-\beta +\alpha )\left\lfloor \frac{b}{c} \right\rfloor +\alpha \ \ t \in [k+1,n] \end{aligned}$$

that do not involve $\mu ^2_k$ and the following families of inequalities that involve $\mu ^2_k$: (97) for $i=2$, (130), (132), (131), (129), (101), (128), (126), (127) and (124).

1.3 Elimination of $\mu ^2_k$

Here we need to combine the four inequalities (97) for $i=2$, (130), (132) and (131) with the six inequalities (129), (101), (128), (126), (127) and (124) to eliminate $\mu ^2_k$.

Combining (97) and (126) gives (90) for $t=k$:

$$\begin{aligned} \sigma _{k} -\sigma _{k-1} \le 0. \end{aligned}$$

Combining (97) and (124) gives for $t\in [k,n]$:

$$\begin{aligned} \sigma _t-(c-\beta )\zeta _t -(\beta -\alpha )\mu ^1_{k-1}-\alpha \mu ^2_{k-1} \le (c-\beta ) \left\lfloor \frac{b}{c} \right\rfloor . \end{aligned}$$

These are inequalities (106) for $t\in [k,n]$.

Combining (130)and (127) for $t=k$ gives:

$$\begin{aligned} \sigma _k-c\zeta _k \le b, \end{aligned}$$

which is (91) for $t=k$.

Combining (130) and (124) for $t=k$ gives

$$\begin{aligned} \sigma _k-(c-\beta +\alpha )\zeta _k -(\beta -\alpha )\mu ^1_{k-1} \le (c-\beta +\alpha )\left\lfloor \frac{b}{c} \right\rfloor +\alpha . \end{aligned}$$

This is (107) for $t=k$. Together with (125), we have (107) for $t\in [k,n]$.

Combining (132) and (101) gives (92) for $t=k$:

$$\begin{aligned} -\sigma _k +c\zeta _k \le -a. \end{aligned}$$

Combining (131) and (101) gives for $t\in [k+1,n]$

$$\begin{aligned} \sigma _t-\sigma _k-(c-\beta +\alpha )(\zeta _t-\zeta _k) \le (c-\beta +\alpha )\left( \left\lfloor \frac{b}{c} \right\rfloor - \left\lfloor \frac{a}{c} \right\rfloor \right) . \end{aligned}$$

These are inequalities (106) since $\left\lfloor \frac{b-a}{c} \right\rfloor = \left\lfloor \frac{b}{c} \right\rfloor - \left\lfloor \frac{a}{c} \right\rfloor$.

The remaining combinations are redundant:

Combining (97) and (129) gives

$$\begin{aligned} \sigma _k-c\mu ^2_{k-1}\le 0. \end{aligned}$$

It is redundant taking $\sigma _{k-1}-(c-\beta )\mu ^0_{k-1}-(\beta -\alpha )\mu ^1_{k-1} -\alpha \mu ^2_{k-1}=0$ with weight 1, $\mu ^0_{k-1}-\mu ^1_{k-1} \le 0$ with weight $(c-\beta )$, $\mu ^1_{k-1}-\mu ^2_{k-1} \le 0$ with weight $(c-\alpha )$ and $-\sigma _{k-1}+\sigma _k \le 0$ with weight 1.

Combining (97) and (101) gives

$$\begin{aligned} -\mu ^2_{k-1}+\zeta _k \le -\left\lfloor \frac{a}{c} \right\rfloor -1. \end{aligned}$$

It is redundant taking $-\zeta _{k-1}+\zeta _k \le 0$ with weight 1 and $\zeta _{k-1}-\mu ^2_{k-1} \le -\left\lfloor \frac{a}{c} \right\rfloor -1$ with weight 1.

Combining (97) and (128) gives

$$\begin{aligned} \sigma _k-(c-\beta )\mu ^0_{k-1}-\beta \mu ^2_{k-1} \le 0. \end{aligned}$$

It is redundant taking $\sigma _{k-1}-(c-\beta )\mu ^0_{k-1}-(\beta -\alpha )\mu ^1_{k-1} -\alpha \mu ^2_{k-1}=0$ with weight 1, $\mu ^1_{k-1}-\mu ^2_{k-1} \le 0$ with weight $(\beta -\alpha )$ and $-\sigma _{k-1}+\sigma _k \le 0$ with weight 1.

Combining (97) and (127) for $t \in [k,n]$ gives

$$\begin{aligned} \sigma _t-(c-\beta )\zeta _t-\beta \mu ^2_{k-1} \le (c-\beta )\left\lfloor \frac{b}{c} \right\rfloor . \end{aligned}$$

It is redundant taking (106) $\sigma _t-(c-\beta )\zeta _t-(\beta -\alpha )\mu ^1_{k-1}-\alpha \mu ^2_{k-1} \le (c-\beta ) \left\lfloor \frac{b}{c} \right\rfloor$ with weight 1 and $\mu ^1_{k-1}-\mu ^2_{k-1} \le 0$ with weight $(\beta - \alpha )$.

Combining (130) and (129) gives

$$\begin{aligned} \sigma _k-c\zeta _k \le c\left( 1+\left\lfloor \frac{b}{c} \right\rfloor \right) . \end{aligned}$$

This is redundant taking $\sigma _k-c\zeta _k \le b.$

Combining (130) and (101) gives

$$\begin{aligned} 0 \le \left\lfloor \frac{b}{c} \right\rfloor -\left\lfloor \frac{a}{c} \right\rfloor . \end{aligned}$$

This is redundant as $a \le b$.

Combining (130) and (128) gives

$$\begin{aligned} \sigma _k-(c-\beta )\mu ^0_{k-1}-\beta \zeta _k \le \beta \left( 1+\left\lfloor \frac{b}{c} \right\rfloor \right) . \end{aligned}$$

This is redundant taking $\sigma _{k-1}-(c-\beta )\mu ^0_{k-1}-(\beta -\alpha )\mu ^1_{k-1} -\alpha \mu ^2_{k-1}=0$ with weight $\frac{c-\beta }{c}$, $\sigma _k-c\zeta _k \le b$ with weight $\frac{\beta }{c}$, $\mu ^1_{k-1}-\mu ^2_{k-1} \le 0$ with weight $\frac{c-\beta }{c}(\beta -\alpha )$, $\mu ^2_{k-1}-\mu ^0_{k-1} \le 1$ with weight $\frac{\beta }{c}(c-\beta )$ and $-\sigma _{k-1}+\sigma _k \le 0$ with weight $\frac{c-\beta }{c}$.

Combining (130) and (126) gives

$$\begin{aligned} \sigma _k-(c-\beta )\mu ^0_{k-1}-(\beta -\alpha )\mu ^1_{k-1}-\alpha \zeta _k \le \alpha \left( 1+\left\lfloor \frac{b}{c} \right\rfloor \right) . \end{aligned}$$

This is redundant taking $-(\beta -\alpha )\mu ^1_{k-1}+\sigma _k-(c-\beta +\alpha ) \zeta _k \le (c-\beta +\alpha ) \left\lfloor \frac{b}{c} \right\rfloor +\alpha$ with weight $\frac{\alpha }{c-\beta +\alpha }$, $\sigma _{k-1}-(c-\beta )\mu ^0_{k-1}-(\beta -\alpha )\mu ^1_{k-1}-\alpha \mu ^2_{k-1}=0$ with weight $\frac{c-\beta }{c-\beta +\alpha }$, $\mu ^2_{k-1}-\mu ^0_{k-1} \le 1$ with weight $\frac{\alpha (c-\beta )}{c-\beta +\alpha }$ and $-\sigma _{k-1}+\sigma _k \le 0$ with weight $\frac{c-\beta }{c-\beta +\alpha }$.

Combining (130) and (127) for $t\in [k+1,n]$ gives

$$\begin{aligned} \sigma _t-(c-\beta )\zeta _t -\beta \zeta _k \le b. \end{aligned}$$

This is redundant taking $\sigma _k-c\zeta _k \le b$ with weight $\frac{\beta }{c}$, $\sigma _t-c\zeta _t \le b$ with weight $\frac{c-\beta }{c}$ and $-\sigma _{j-1}+\sigma _j \le 0$ with weight $\frac{\beta }{c}$ for $j \in [k+1,t]$.

Combining (130) and (124) for $t\in [k+1,n]$ gives

$$\begin{aligned} \sigma _t-(c-\beta )\zeta _t -(\beta -\alpha )\mu ^1_{k-1}-\alpha \zeta _k \le (c-\beta +\alpha )\left\lfloor \frac{b}{c} \right\rfloor +\alpha . \end{aligned}$$

This is redundant taking ((107) for k) $-(\beta -\alpha )\mu ^1_{k-1}+\sigma _k -(c-\beta +\alpha )\zeta _k \le (c-\beta +\alpha )\left\lfloor \frac{b}{c} \right\rfloor +\alpha$ with weight $\frac{\alpha }{c-\beta +\alpha }$, ((107) for t) $-(\beta -\alpha )\mu ^1_{k-1}+\sigma _t -(c-\beta +\alpha )\zeta _t \le (c-\beta +\alpha )\left\lfloor \frac{b}{c} \right\rfloor +\alpha$ with weight $1-\frac{\alpha }{c-\beta +\alpha }$ and $-\sigma _{j-1}+\sigma _j \le 0$ with weight$\frac{\alpha }{c-\beta +\alpha }$ for $j \in [k+1,t]$.

Combining (132) and (129) gives

$$\begin{aligned} c-\alpha \ge 0 \end{aligned}$$

which is redundant.

Combining (132) and (128) gives

$$\begin{aligned} (c-\beta )\sigma _k-(c-\beta )c\mu ^0_{k-1}\le (c-\alpha )\beta . \end{aligned}$$

This is redundant taking $\sigma _{k-1}- (c-\beta )\mu ^0_{k-1}-(\beta -\alpha )\mu ^1_{k-1}-\alpha \mu ^2_{k-1}=0$ with weight $(c-\beta )$, $\mu ^1_{k-1}-\mu ^2_{k-1} \le 0$ with weight $(c-\beta )(\beta -\alpha )$, $\mu ^2_{k-1}-\mu ^0_{k-1} \le 1$ with weight $(c-\beta )\beta$, $-\sigma _{k-1}+\sigma _k \le 0$ with weight $(c-\beta )$and $(c-\beta )\beta \le (c-\alpha )\beta$ with weight 1.

Combining (132) and (126) gives

$$\begin{aligned} (c-\alpha )\sigma _k-c(c-\beta )\mu ^0_{k-1}-c(\beta -\alpha )\mu ^1_{k-1} \le \alpha (c-\alpha ). \end{aligned}$$

This is redundant taking $\sigma _{k-1}- (c-\beta )\mu ^0_{k-1}-(\beta -\alpha )\mu ^1_{k-1}-\alpha \mu ^2_{k-1}=0$ with weight $(c-\alpha )$, $\mu ^0_{k-1}-\mu ^1_{k-1} \le 0$ with weight $\alpha (\beta -\alpha )$, $\mu ^2_{k-1}-\mu ^0_{k-1} \le 1$ with weight $\alpha (c-\alpha )$ and $-\sigma _{k-1}+\sigma _k \le 0$ with weight $(c-\alpha )$.

Combining (132) and (127) for $t\in [k,n]$ gives

$$\begin{aligned} c\sigma _t-c(c-\beta )\zeta _t -\beta \sigma _k \le \beta (c-\alpha )+(c-\beta )c\left\lfloor \frac{b}{c} \right\rfloor . \end{aligned}$$

This is redundant taking $\sigma _t-c\zeta _t \le b$ with weight $(c-\beta )$, $-\sigma _{j-1}+\sigma _j \le 0$ with weight $\beta$ for $j \in [k+1,t]$, $b(c-\beta )= \beta (c-\beta )+(c-\beta )c\left\lfloor \frac{b}{c} \right\rfloor$ with weight 1 and $\beta (c-\beta ) \le \beta (c-\alpha )$ with weight 1.

Combining (132) and (124) for $t\in [k,n]$ gives

$$\begin{aligned} c\sigma _t- c(c-\beta )\zeta _t -\alpha \sigma _k-c(\beta -\alpha )\mu ^1_{k-1} \le c(c-\beta )\left\lfloor \frac{b}{c} \right\rfloor +(c-\alpha )\alpha . \end{aligned}$$

This is redundant taking ((107) for t) $\sigma _t-(c-\beta +\alpha )\zeta _t - (\beta -\alpha )\mu ^1_{k-1} \le (c-\beta +\alpha )\left\lfloor \frac{b}{c} \right\rfloor +\alpha$ with weight $\frac{c(c-\beta )}{c-\beta +\alpha }$, $\sigma _{k-1}- (c-\beta )\mu ^0_{k-1}-(\beta -\alpha )\mu ^1_{k-1}-\alpha \mu ^2_{k-1}=0$ with weight $\frac{\alpha (\beta -\alpha )}{c-\beta +\alpha }$, $\mu ^0_{k-1}-\mu ^1_{k-1} \le 0$ with weight $\alpha (\beta -\alpha )$, $\mu ^2_{k-1}-\mu ^0_{k-1} \le 1$ with weight $\frac{\alpha ^2(\beta -\alpha )}{c-\beta +\alpha }$, $-\sigma _{k-1}+\sigma _k \le 0$ with weight $\frac{\alpha (\beta -\alpha )}{c-\beta +\alpha }$ and $-\sigma _{j-1}+\sigma _j \le 0$ with weight $\frac{\alpha c}{c-\beta +\alpha }$ for $j \in [k+1,t]$.

Combining (131) for $t\in [k+1,n]$ and (129) gives

$$\begin{aligned} c\sigma _t-c(c-\beta +\alpha )\zeta _t-(\beta -\alpha )\sigma _k \le c(c-\beta +\alpha )\left( \left\lfloor \frac{b}{c} \right\rfloor +1\right) . \end{aligned}$$

This is redundant taking $-\sigma _{j-1}+\sigma _j \le 0$ with weight $(\beta -\alpha )$ for $j \in [k+1,t]$, $\sigma _t-c\zeta _t \le b$ with weight $(c-\beta +\alpha )$ and $\beta \le c$ with weight $c-\beta +\alpha$.

Combining (131) for $t\in [k+1,n]$ and (128) gives

$$\begin{aligned}&\beta \sigma _t-\beta (c-\beta +\alpha )\zeta _t +(c-2\beta +\alpha )\sigma _k -(c-\beta +\alpha )(c-\beta )\mu ^0_{k-1}\\&\quad \le \beta (c-\beta +\alpha )\left( \left\lfloor \frac{b}{c} \right\rfloor +1\right) . \end{aligned}$$

Case 1. $c-2\beta +\alpha \ge 0$

This is redundant taking ((107) for t) $\sigma _t-(c-\beta +\alpha )\zeta _t-(\beta -\alpha )\mu ^1_{k-1} \le (c-\beta +\alpha ) \left\lfloor \frac{b}{c} \right\rfloor +\alpha$ with weight $\beta$, $\sigma _{k-1}-(c-\beta )\mu ^0_{k-1}-(\beta -\alpha )\mu ^1_{k-1} -\alpha \mu ^2_{k-1} =0$ with weight $c-2\beta +\alpha$, $\mu ^1_{k-1}-\mu ^2_{k-1} \le 0$ with weight $(\beta -\alpha )(c-\beta +\alpha )$, $-\mu ^0_{k-1}+\mu ^2_{k-1} \le 1$ with weight $\beta (c-\beta )$ and $-\sigma _{k-1}+\sigma _k \le 0$ with weight $c-2\beta +\alpha$.

Case 2. $c-2\beta +\alpha < 0$

This is redundant taking $\sigma _t-c \zeta _t \le b$ with weight $\frac{(c-\beta +\alpha )(2 \beta -c-\alpha )}{\beta -\alpha }$, $\sigma _t-(c-\beta +\alpha )\zeta _t-(\beta -\alpha )\mu ^1_{k-1} \le (c-\beta +\alpha ) \left\lfloor \frac{b}{c} \right\rfloor +\alpha$ with weight $\frac{(c-\beta +\alpha )(c-\beta )}{\beta -\alpha }$, $\mu ^1_{k-1}-\mu ^2_{k-1} \le 0$ with weight $(c-\beta )(c-\beta +\alpha )$, $-\mu ^0_{k-1}+\mu ^2_{k-1} \le 1$ with weight $(c-\beta )(c-\beta +\alpha )$and $-\sigma _{j-1}+\sigma _j \le 0$ for $j \in [k+1,t]$ with weight $2 \beta -c-\alpha$.

Combining (131) for $t\in [k+1,n]$ and (126) gives

$$\begin{aligned}&\alpha \sigma _t +(c-\beta )\sigma _k-(c-\beta +\alpha )\left( \alpha \zeta _t+(c-\beta )\mu ^0_{k-1}+(\beta -\alpha )\mu ^1_{k-1}\right) \\&\quad \le \alpha (c-\beta +\alpha )\left( \left\lfloor \frac{b}{c} \right\rfloor +1\right) . \end{aligned}$$

This is redundant taking ((107) for t) $-(\beta -\alpha )\mu ^1_{k-1}+\sigma _t-(c-\beta +\alpha )\zeta _t \le (c-\beta +\alpha )\left\lfloor \frac{b}{c} \right\rfloor +\alpha$ with weight $\alpha$, $\sigma _{k-1}- (c-\beta )\mu ^0_{k-1}-(\beta -\alpha )\mu ^1_{k-1}-\alpha \mu ^2_{k-1}=0$ with weight $(c-\beta )$, $\mu ^2_{k-1}-\mu ^0_{k-1} \le 1$ with weight $\alpha (c-\beta )$ and $-\sigma _{k-1}+\sigma _k \le 0$ with weight $(c-\beta )$.

Combining (131) for $t\in [k+1,n]$ and (127) for $q\in [k,n]$ gives

$$\begin{aligned} \beta [\sigma _t-(c-\beta +\alpha )\zeta _t]+(c-\beta +\alpha )[\sigma _q-(c-\beta )\zeta _q] -\beta \sigma _k \le (c-\beta +\alpha )b. \end{aligned}$$

Case 1. $t>q$

This is redundant taking $\sigma _t-c\zeta _t \le b$ with weight $(c-\beta +\alpha )\beta /c$, $\sigma _q-c\zeta _q \le b$ with weight $(c-\beta +\alpha )(c-\beta )/c$, $-\sigma _{j-1}+\sigma _j \le 0$ with weight $\beta$ for $j \in [k+1,q]$ and $-\sigma _{j-1}+\sigma _j \le 0$ with weight $\beta (\beta -\alpha )/c$ for $j \in [q+1,t]$.

Case 2. $t\le q$

This is redundant taking $\sigma _t-c\zeta _t \le b$ with weight $(c-\beta +\alpha )\beta /c$, $\sigma _q-c\zeta _q \le b$ with weight $(c-\beta +\alpha )(c-\beta )/c$, $-\sigma _{j-1}+\sigma _j \le 0$ with weight $\beta$ for $j \in [k+1,t]$ and $-\sigma _{j-1}+\sigma _j \le 0$ with weight $\beta (c-\beta +\alpha )/c$ for $j \in [t+1,q]$.

Combining (131) for $t \in [k+1,n]$ and (124) for $q \in [k,n]$ gives

$$\begin{aligned}&\alpha [\sigma _t-(c-\beta +\alpha )\zeta _t] +(c-\beta +\alpha )[\sigma _q-(c-\beta )\zeta _q]\\&\quad -\alpha \sigma _k-(c-\beta +\alpha )(\beta -\alpha )\mu ^1_{k-1} \le (c-\beta +\alpha )[(c-\beta +\alpha )\left\lfloor \frac{b}{c} \right\rfloor + \alpha ]. \end{aligned}$$

This is redundant taking ((107) for t) $-(\beta -\alpha ) \mu ^1_{k-1}+\sigma _t-(c-\beta +\alpha )\zeta _t \le (c-\beta +\alpha )\left\lfloor \frac{b}{c} \right\rfloor +\alpha$ with weight $\alpha$, ((107) for q) $-(\beta -\alpha ) \mu ^1_{k-1}+\sigma _q-(c-\beta +\alpha )\zeta _q \le (c-\beta +\alpha )\left\lfloor \frac{b}{c} \right\rfloor +\alpha$ with weight $(c-\beta )$ and $-\sigma _{j-1}+\sigma _j \le 0$ with weight $\alpha$ for $j \in [k+1,q]$.

The iteration is complete and we obtain the formulation with k replaced by $k-1$.

$\square$