Skip to main content
SpringerLink
Log in

Maximum edge-disjoint paths in planar graphs with congestion 2

  • Full Length Paper
  • Series A
  • Published:
Mathematical Programming Submit manuscript

Abstract

We study the maximum edge-disjoint path problem (medp) in planar graphs \(G=(V,E)\) with edge capacities u(e). We are given a set of terminal pairs \(s_it_i\), \(i=1,2 \ldots , k\) and wish to find a maximum routable subset of demands. That is, a subset of demands that can be connected by a family of paths that use each edge at most u(e) times. It is well-known that there is an integrality gap of \(\Omega (\sqrt{n})\) for the natural LP relaxation, even in planar graphs (Garg–Vazirani–Yannakakis). We show that if every edge has capacity at least 2, then the integrality gap drops to a constant. This result is tight also in a complexity-theoretic sense: recent results of Chuzhoy–Kim–Nimavat show that it is unlikely that there is any polytime-solvable LP formulation for medp which has a constant integrality gap for planar graphs. Along the way, we introduce the concept of rooted clustering which we believe is of independent interest.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Notes

  1. One may relax the condition that a terminal’s demand is assigned to only one cluster. A splittable rooted clustering is one where a demand of \(d_i\) may be split across multiple clusters.

  2. If G is undirected, we bi-direct edges and “trim” t to be a sink.

  3. Their set-up is slightly different (e.g., they only consider bounded degree graphs) consider planar graphs and clusters being but their ideas easily yield this general result.

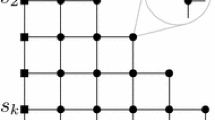
  4. This is essentially the same as one given in [7] as an example of a \(\Omega (\log n)\) gap for the congestion minimization LP for confluent flows.

  5. One could also consider splittable clusterings where a fraction of the demand is assigned across several clusters. We do not need to resort to this version.

  6. The notation \(\delta (X)\) represents the set of edges in the bipartite graph with exactly one endpoint in X.

  7. Informally, a contour is a closed simple curve in the plane; we refer the reader to texts in algebraic topology for more formality as needed.

References

  1. Andrews, M.: Approximation algorithms for the edge-disjoint paths problem via Räcke decompositions. In: 2010 IEEE 51st Annual Symposium on Foundations of Computer Science, pp. 277–286 (2010)

  2. Andrews, M., Chuzhoy, J., Guruswami, V., Khanna, S., Talwar, K., Zhang, L.: Inapproximability of edge-disjoint paths and low congestion routing on undirected graphs. Combinatorica 30(5), 485–520 (2010)

    Article  MathSciNet  Google Scholar 

  3. Chekuri, C., Khanna, S., Shepherd, F.B.: Edge-disjoint paths in planar graphs. In: 45th Annual IEEE Symposium on Foundations of Computer Science, 2004. Proceedings, pp. 71–80 (2004)

  4. Chekuri, C., Chuzhoy, J.: Maximum node-disjoint paths with congestion 2. Personal communication (2016)

  5. Chekuri, C., Khanna, S., Bruce Shepherd, F.: Edge-disjoint paths in planar graphs with constant congestion. In: STOC ’06: Proceedings of the Thirty-Eighth Annual ACM Symposium on Theory of Computing, pp. 757–766. ACM, New York, NY (2006)

  6. Chekuri, C., Naves, G., Bruce Shepherd, F.: Maximum edge-disjoint paths in k-sums of graphs. In: International Colloquium on Automata, Languages, and Programming, pp. 328–339. Springer (2013)

  7. Chen, J., Kleinberg, R.D., Lovász, L., Rajaraman, R., Sundaram, R., Vetta, A.: (Almost) tight bounds and existence theorems for single-commodity confluent flows. J. ACM 54(4), 16 (2007)

    Article  MathSciNet  Google Scholar 

  8. Chuzhoy, J.: Routing in undirected graphs with constant congestion. In: Proceedings of the 44th Symposium on Theory of Computing, pp. 855–874. ACM (2012)

  9. Chuzhoy, J., Li, S.: A polylogarithimic approximation algorithm for edge-disjoint paths with congestion 2. arXiv preprint arXiv:1208.1272 (2012)

  10. Chuzhoy, J., Kim, D.H.K., Nimavat, R.: New hardness results for routing on disjoint paths. arXiv preprint arXiv:1611.05429 (2016)

  11. Cook, W.J., Cunningham, W.H., Pulleyblank, W.R., Schrijver, A.: Combinatorial Optimization. Wiley-Interscience, Hoboken (1997)

    Book  Google Scholar 

  12. Dinitz, Y., Garg, N., Goemans, M.X.: On the single-source unsplittable flow problem. Combinatorica 19(1), 17, 01–41 (1999)

    Article  MathSciNet  Google Scholar 

  13. Donovan, P., Shepherd, B., Vetta, A., Wilfong, G.: Degree-constrained network flows. In: Proceedings of the Thirty-Ninth Annual ACM Symposium on Theory of computing, pp. 681–688. ACM (2007)

  14. Frank, A.: Packing paths, cuts, and circuits—a survey. In: Korte, B., Lovász, L., Prömel, H.J., Schrijver, A. (eds.) Paths, Flows and VLSI-Layout, pp. 49–100. Springer, Berlin (1990)

    Google Scholar 

  15. Frank, A.: Connections in Combinatorial Optimization. Oxford University Press, Oxford (2011)

    MATH  Google Scholar 

  16. Garg, N., Vazirani, V.V., Yannakakis, M.: Primal-dual approximation algorithms for integral flow and multicut in trees. Algorithmica 18(1), 3–20 (1997)

    Article  MathSciNet  Google Scholar 

  17. Guruswami, V., Khanna, S., Rajaraman, R., Shepherd, B., Yannakakis, M.: Near-optimal hardness results and approximation algorithms for edge-disjoint paths and related problems. J. Comput. Syst. Sci. 67(3), 473–496 (2003)

    Article  MathSciNet  Google Scholar 

  18. Kawarabayashi, K., Kobayashi, Y.: All-or-nothing multicommodity flow problem with bounded fractionality in planar graphs. SIAM J. Comput. 47(4), 1483–1504 (2018)

    Article  MathSciNet  Google Scholar 

  19. Kleinberg, J., Tardos, É.: Approximations for the disjoint paths problem in high-diameter planar networks. In: Proceedings of the Twenty-Seventh Annual ACM Symposium on Theory of Computing, pp. 26–35. ACM (1995)

  20. Kleinberg, J.M.: An approximation algorithm for the disjoint paths problem in even-degree planar graphs. In: FOCS ’05: Proceedings of the 45th Annual IEEE Symposium on Foundations of Computer Science, pp. 627–636 (2005)

  21. Okamura, H., Seymour, P.D.: Multicommodity flows in planar graphs. J. Combin. Theory Ser. B 31(1), 75–81 (1981)

    Article  MathSciNet  Google Scholar 

  22. Raghavan, P., Thompson, C.D.: Randomized rounding: a technique for provably good algorithms and algorithmic proofs. Combinatorica 7, 365–374 (1987)

    Article  MathSciNet  Google Scholar 

  23. Seguin-Charbonneau, L., Shepherd, F.B.: Maximum edge-disjoint paths in planar graphs with congestion 2. In: 2011 IEEE 52nd Annual Symposium on Foundations of Computer Science (FOCS), pp. 200–209. IEEE (2011)

Download references

Acknowledgements

The authors are grateful for excellent feedback from three anonymous referees. The second author thanks Chandra Chekuri for many stimulating conversations on this and related topics. This work has been primarily supported by an NSERC Discovery Grant.

Author information

Authors and Affiliations

  1. Cégep Édouard Montpetit, Longueuil, QC, Canada

    Loïc Séguin-Charbonneau

  2. Department of Computer Science, University of British Columbia, Vancouver, BC, Canada

    F. Bruce Shepherd

Authors
  1. Loïc Séguin-Charbonneau
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. F. Bruce Shepherd
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to F. Bruce Shepherd.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Séguin-Charbonneau, L., Shepherd, F.B. Maximum edge-disjoint paths in planar graphs with congestion 2. Math. Program. 188, 295–317 (2021). https://doi.org/10.1007/s10107-020-01513-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10107-020-01513-1

Keywords

Mathematics Subject Classification

Search

Navigation