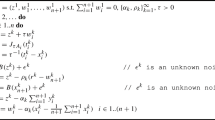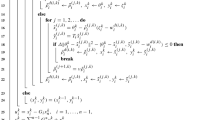Skip to main content
Springer Nature Link
Log in

Projective splitting with forward steps

  • Full Length Paper
  • Series A
  • Published:
Mathematical Programming Submit manuscript

Abstract

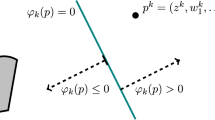
This work is concerned with the classical problem of finding a zero of a sum of maximal monotone operators. For the projective splitting framework recently proposed by Combettes and Eckstein, we show how to replace the fundamental subproblem calculation using a backward step with one based on two forward steps. The resulting algorithms have the same kind of coordination procedure and can be implemented in the same block-iterative and highly flexible manner, but may perform backward steps on some operators and forward steps on others. Prior algorithms in the projective splitting family have used only backward steps. Forward steps can be used for any Lipschitz-continuous operators provided the stepsize is bounded by the inverse of the Lipschitz constant. If the Lipschitz constant is unknown, a simple backtracking linesearch procedure may be used. For affine operators, the stepsize can be chosen adaptively without knowledge of the Lipschitz constant and without any additional forward steps. We close the paper by empirically studying the performance of several kinds of splitting algorithms on a large-scale rare feature selection problem.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Alotaibi, A., Combettes, P.L., Shahzad, N.: Solving coupled composite monotone inclusions by successive Fejér approximations of their Kuhn-Tucker set. SIAM J. Optim. 24(4), 2076–2095 (2014)

    Article  MathSciNet  Google Scholar 

  2. Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces, 2nd edn. Springer, Berlin (2017)

    Book  Google Scholar 

  3. Beck, A., Teboulle, M.: Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans. Image Process. 18(11), 2419–2434 (2009)

    Article  MathSciNet  Google Scholar 

  4. Boyd, S., Parikh, N., Chu, E., Peleato, B., Eckstein, J.: Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 3(1), 1–122 (2011)

    Article  Google Scholar 

  5. Briceño-Arias, L.M., Combettes, P.L.: A monotone+ skew splitting model for composite monotone inclusions in duality. SIAM J. Optim. 21(4), 1230–1250 (2011)

    Article  MathSciNet  Google Scholar 

  6. Chambolle, A., Pock, T.: A first-order primal-dual algorithm for convex problems with applications to imaging. J. Math. Imaging Vis. 40(1), 120–145 (2011)

    Article  MathSciNet  Google Scholar 

  7. Combettes, P.L.: Fejér monotonicity in convex optimization. In: Encyclopedia of optimization, vol. 2, pp. 106–114. Springer (2001)

  8. Combettes, P.L., Eckstein, J.: Asynchronous block-iterative primal-dual decomposition methods for monotone inclusions. Math. Program. 168(1–2), 645–672 (2018)

    Article  MathSciNet  Google Scholar 

  9. Combettes, P.L., Pesquet, J.C.: Proximal splitting methods in signal processing. In: Fixed-Point Algorithms for Inverse Problems in Science and Engineering, pp. 185–212. Springer (2011)

  10. Combettes, P.L., Pesquet, J.C.: Primal-dual splitting algorithm for solving inclusions with mixtures of composite, Lipschitzian, and parallel-sum type monotone operators. Set-Valued Var. Anal. 20(2), 307–330 (2012)

    Article  MathSciNet  Google Scholar 

  11. Combettes, P.L., Vũ, B.C.: Variable metric forward-backward splitting with applications to monotone inclusions in duality. Optimization 63(9), 1289–1318 (2014)

    Article  MathSciNet  Google Scholar 

  12. Combettes, P.L., Wajs, V.R.: Signal recovery by proximal forward–backward splitting. Multiscale Model. Simul. 4(4), 1168–1200 (2005)

    Article  MathSciNet  Google Scholar 

  13. Condat, L.: A primal-dual splitting method for convex optimization involving Lipschitzian, proximable and linear composite terms. J. Optim. Theory Appl. 158(2), 460–479 (2013)

    Article  MathSciNet  Google Scholar 

  14. Davis, D., Yin, W.: A three-operator splitting scheme and its optimization applications. Set-Valued Var. Anal. 25(4), 829–858 (2017)

    Article  MathSciNet  Google Scholar 

  15. Eckstein, J.: A simplified form of block-iterative operator splitting and an asynchronous algorithm resembling the multi-block alternating direction method of multipliers. J. Optim. Theory Appl. 173(1), 155–182 (2017)

    Article  MathSciNet  Google Scholar 

  16. Eckstein, J., Svaiter, B.F.: A family of projective splitting methods for the sum of two maximal monotone operators. Math. Program. 111(1), 173–199 (2008)

    MathSciNet  MATH  Google Scholar 

  17. Eckstein, J., Svaiter, B.F.: General projective splitting methods for sums of maximal monotone operators. SIAM J. Control Optim. 48(2), 787–811 (2009)

    Article  MathSciNet  Google Scholar 

  18. Eckstein, J., Yao, W.: Approximate ADMM algorithms derived from Lagrangian splitting. Comput. Optim. Appl. 68(2), 363–405 (2017)

    Article  MathSciNet  Google Scholar 

  19. Eckstein, J., Yao, W.: Relative-error approximate versions of Douglas-Rachford splitting and special cases of the ADMM. Math. Program. 170(2), 417–444 (2018)

    Article  MathSciNet  Google Scholar 

  20. Iusem, A., Svaiter, B.: A variant of Korpelevich’s method for variational inequalities with a new search strategy. Optimization 42(4), 309–321 (1997)

    Article  MathSciNet  Google Scholar 

  21. Johnstone, P.R., Eckstein, J.: Convergence rates for projective splitting. SIAM J. Optim. 29(3), 1931–1957 (2019)

    Article  MathSciNet  Google Scholar 

  22. Komodakis, N., Pesquet, J.C.: Playing with duality: an overview of recent primal-dual approaches for solving large-scale optimization problems. IEEE Signal Process. Mag. 32(6), 31–54 (2015)

    Article  Google Scholar 

  23. Korpelevich, G.: The extragradient method for finding saddle points and other problems. Matecon 12, 747–756 (1976)

    MathSciNet  MATH  Google Scholar 

  24. Krasnosel’skii, M.A.: Two remarks on the method of successive approximations. Uspekhi Matematicheskikh Nauk 10(1), 123–127 (1955)

    MathSciNet  Google Scholar 

  25. Lions, P.L., Mercier, B.: Splitting algorithms for the sum of two nonlinear operators. SIAM J. Numer. Anal. 16(6), 964–979 (1979)

    Article  MathSciNet  Google Scholar 

  26. Malitsky, Y., Pock, T.: A first-order primal-dual algorithm with linesearch. SIAM J. Optim. 28(1), 411–432 (2018)

    Article  MathSciNet  Google Scholar 

  27. Malitsky, Y., Tam, M.K.: A forward-backward splitting method for monotone inclusions without cocoercivity. arXiv preprint arXiv:1808.04162 (2018)

  28. Mann, W.R.: Mean value methods in iteration. Proc. Am. Math. Soc. 4(3), 506–510 (1953)

    Article  MathSciNet  Google Scholar 

  29. Mercier, B., Vijayasundaram, G.: Lectures on Topics in Finite Element Solution of Elliptic Problems. Tata Institute of Fundamental Research, Bombay (1979)

    Book  Google Scholar 

  30. Nocedal, J.: Updating quasi-Newton matrices with limited storage. Math. Comp. 35(151), 773–782 (1980)

    Article  MathSciNet  Google Scholar 

  31. Pedregosa, F., Gidel, G.: Adaptive three operator splitting. Tech. Rep. arXiv:1804.02339, arXiv (2018)

  32. Solodov, M.V., Svaiter, B.F.: A hybrid projection-proximal point algorithm. J. Convex Anal. 6(1), 59–70 (1999)

    MathSciNet  MATH  Google Scholar 

  33. Solodov, M.V., Svaiter, B.F.: A new projection method for variational inequality problems. SIAM J. Control Optim. 37(3), 765–776 (1999)

    Article  MathSciNet  Google Scholar 

  34. Tran-Dinh, Q., Vũ, B.C.: A new splitting method for solving composite monotone inclusions involving parallel-sum operators. Preprint arXiv:1505.07946, arXiv (2015)

  35. Tseng, P.: A modified forward-backward splitting method for maximal monotone mappings. SIAM J. Control Optim. 38(2), 431–446 (2000)

    Article  MathSciNet  Google Scholar 

  36. Vũ, B.C.: A splitting algorithm for dual monotone inclusions involving cocoercive operators. Adv. Comput. Math. 38(3), 667–681 (2013)

    Article  MathSciNet  Google Scholar 

  37. Vũ, B.C.: A variable metric extension of the forward–backward–forward algorithm for monotone operators. Numer. Funct. Anal. Optim. 34(9), 1050–1065 (2013)

    Article  MathSciNet  Google Scholar 

  38. Yan, X., Bien, J.: Rare Feature Selection in High Dimensions. arXiv preprint arXiv:1803.06675 (2018)

Download references

Acknowledgements

This material is based upon work supported by the National Science Foundation under Grant No. 1617617. We thank Xiaohan Yan and Jacob Bien for kindly sharing their data for the TripAdvisor reviews problem in Sect. 6.

Author information

Authors and Affiliations

  1. Department of Management Sciences and Information Systems, Rutgers Business School, Rutgers University, Newark, New Brunswick, USA

    Patrick R. Johnstone & Jonathan Eckstein

Authors
  1. Patrick R. Johnstone
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jonathan Eckstein
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Patrick R. Johnstone.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Johnstone, P.R., Eckstein, J. Projective splitting with forward steps. Math. Program. 191, 631–670 (2022). https://doi.org/10.1007/s10107-020-01565-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10107-020-01565-3

Mathematics Subject Classification