Decomposition of loosely coupled integer programs: a multiobjective perspective

Abstract

We consider integer programming (IP) problems consisting of (possibly a large number of) subsystems and a small number of coupling constraints that link variables from different subsystems. Such problems are called loosely coupled or nearly decomposable. In this paper, we exploit the idea of resource-directive decomposition to reformulate the problem so that it can be decomposed into a resource-directive master problem and a set of multiobjective programming subproblems. Recent methods developed for solving multiobjective problems enable us to formulate a relaxation of the master problem that is an IP whose solution yields a dual bound on the value of the original IP. This perspective provides a new, general framework for IP decomposition, in which many alternative algorithm designs are possible. Here, we develop one such algorithm, and demonstrate its viability and potential benefits with the aid of computational experiments knapsack-based instances with up to five coupling constraints and 7500 variables, comparing it with both a standard IP solver and a generic branch-and-price solver.

Appendices

Proofs

1.1 Proof of Lemma 1

Let $z\in {\mathbb {R}}^J$ be an NDP of (13), and, for contradiction, assume that $z$ is not an NDP of (4). As $z$ is clearly feasible for (4) and assumed not to be an NDP, there must exist $x' \in {\mathcal {X}}$ with $z' = (g_1(x'),\ldots ,g_J(x')) \le z$ and $z' \ne z$. Then, combining this with (13c), we obtain $z'_j = g_j(x') \le z_j \le \delta _j$ for all $j \in {\mathcal {J}}'$. This implies that $z'$ is also feasible for (13), which contradicts the fact that $z$ is an NDP of (13). $\square$

1.2 Proof of Proposition 1

Let $\{u^i\}_{i \in \mathcal {M}}$ be an arbitrary optimal solution of RDMP, and, for each $i \in \mathcal {M}$, let ${\hat{x}}^i$ be an optimal solution of the $i{\text {th}}$ subproblem RDSP($i,u$). Without loss of generality, we may take ${\hat{x}}^i$ to be an optimal solution such that $A^i{\hat{x}}^i$ is not dominated by $A^ix^i$ for any other optimal solution $x^i$, for example, take ${\hat{x}}^i$ to be an optimal solution of

$$\begin{aligned} \mathop {{{\,\mathrm{lex\,min \ }\,}}}\limits _{x\in {\mathcal {X}}^i: A^ix\le u^i} \left( (c^i)^\top x, A^i_1 x, \ldots , A^i_mx\right) . \end{aligned}$$

Let ${\hat{u}}^i:= A^i{\hat{x}}^i$ for all $i \in \mathcal {M}$. Then, $f_i({\hat{u}}^i) = (c^i)^\top {\hat{x}}^i= f_i(u^i)$, and $({\hat{u}}^i,f_i({\hat{u}}^i))$ is the criterion space image of ${\hat{x}}^i$, thus a feasible solution to MOP$(i)$. Also, by construction of ${\hat{x}}^i$ and Lemma 1, it must be that $({\hat{u}}^i,f_i({\hat{u}}^i))$ is an NDP for MOP$(i)$. Lastly, we observe that $\{{\hat{u}}^i\}_{i \in \mathcal {M}}$ is feasible for RDMP since

$$\begin{aligned} \sum _{i \in \mathcal {M}}{\hat{u}}^i= \sum _{i \in \mathcal {M}}A^i{\hat{x}}^i\le \sum _{i \in \mathcal {M}}u^i\le b, \end{aligned}$$

and has the same objective value as that of $\{u^i\}_{i \in \mathcal {M}}$ as

$$\begin{aligned} \sum _{i \in \mathcal {M}}f_i({\hat{u}}^i) = \sum _{i \in \mathcal {M}}(c^i)^\top {\hat{x}}^i= \sum _{i \in \mathcal {M}}f_i(u^i), \end{aligned}$$

which completes the proof. $\square$

1.3 Relationship with value function reformulation

To establish the relationship between our multiobjective reformulation and the value function reformulation discussed in [37], we first adapt the definition of a level-set minimal vector given as Definition 1 in [37] to the context of the RDSP(i, u): the direction of the defining inequality is reversed, since [37] have a maximization problem, whereas RDSP(i, u) is a minimization problem.

Definition 1

Without loss of generality, assume that for given $i\in {{{\mathcal {M}}}}$ all entries of $A^i$ are integer. Then ${{\hat{u}}}\in {\mathbb {Z}}^{n_i}$ is level-set minimal for RDSP(i, u) if $f_i({{\hat{u}}} - {\mathbf {e}}_h) > f_i({{\hat{u}}})$ for all $h=1,\dots , n_i$, where ${\mathbf {e}}_h$ is the hth unit vector.

Proposition 4

The pair $(u^i,f_i(u^i)) \in {{{\mathcal {N}}}}^i$ if and only if $u^i$ is level-set minimal for RDSP(i, u).

Proof

Suppose first that $u^i$ is not level-set minimal for RDSP(i, u). Then for some h it must be that $f_i(u^i-{\mathbf {e}}_h) \le f_i(u^i)$. So there must exist an optimal solution, y say, of RDSP$(i,u^i-{\mathbf {e}}_h)$, with $f_i(u^i-{\mathbf {e}}_h) = (c^i)^{\hat{T}} y$. By feasibility of y, $A^i y \le u^i-{\mathbf {e}}_h \le u^i$ with $u^i-{\mathbf {e}}_h \ne u^i$ and hence $A^i y \ne u^i$. Thus $(A^iy,(c^i)^T y)$ dominates $(u^i,f_i(u^i))$, and so $(u^i,f_i(u^i))\not \in {{{\mathcal {N}}}}^i$.

Now suppose that $(u^i,f_i(u^i))\not \in {{{\mathcal {N}}}}^i$, where $u^i\in {\mathbb {Z}}^{n_i}$. Then there exists ${{\hat{u}}}$ with $({{\hat{u}}},f_i({{\hat{u}}}))\in {{{\mathcal {N}}}}^i$ and $({{\hat{u}}},f_i({{\hat{u}}}))\le (u^i,f_i(u^i))$. Hence ${{\hat{u}}}\ne u^i$. Since $A^i$ is integer (and ${{{\mathcal {X}}}}^i\subseteq {\mathbb {Z}}^{n_i}_+$), ${{\hat{u}}}\in {\mathbb {Z}}^{n_i}$ so ${{\hat{u}}}\le u^i-{\mathbf {e}}_h$ for some $h=1,\dots ,n_i$. Since the value function $f_i$ is monotonically non-increasing, it must be that $f_i({{\hat{u}}}) \ge f_i(u^i-{\mathbf {e}}_h)$. As $f_i(u^i) \ge f_i({{\hat{u}}})$, we have that $f_i(u^i) \ge f_i(u^i-{\mathbf {e}}_h)$ and so $u^i$ is not level-set minimal. $\square$

1.4 Proof of Proposition 2

Given an optimal solution ${\tilde{\lambda }}$ of (7), let $k_i$ be the index such that ${\tilde{\lambda }}^i_{k_i} = 1$ for $i \in \mathcal {M}$. Now, we will construct a feasible solution $({\hat{\lambda }},{\hat{\mu }},{\hat{u}},{\hat{w}})$ to (17). For any $i \in \mathcal {M}$, if $k_i \le |{{\mathcal {P}}}^i|$, let ${\hat{\lambda }}^i_{k_i} = 1$, otherwise let ${\hat{\mu }}^i_{r_i} = 1$, where $r_i \in \{ 1,\ldots , q_i\}$ is an arbitrary index of a region that includes the nondominated point $z^{i,k_i}$. (Such a region exists, by (14).) In the latter case, we also let ${\hat{u}}^{i,r_i} = z^{i,k_i}_{[m]}$ and ${\hat{w}}^i_{r_i} = z^{i,k_i}_{m+1}$. We set all other variable values to zero. Then, (17b)–(17g) hold and the objective function (17a) takes value $\nu ^{IP}$ at $({\hat{\lambda }},{\hat{\mu }},{\hat{u}},{\hat{w}})$. $\square$

1.5 Proof of Proposition 3

Given the conditions of the proposition, we will construct a feasible solution to the LP dual of a relaxation of the LP relaxation of (LB-M), with value equal to $\nu ^{IP}_{LP}$. Since ${{\hat{\gamma }}}$ and $\{{\hat{\alpha }_i\}}_{i \in \mathcal {M}}$ are the optimal dual variables for the LP relaxation of (IP-M), it must be that

$$\begin{aligned} z_{m+1} - {{\hat{\gamma }}}^{\hat{\mathsf {T}}} z_{[m]} - {\hat{\alpha }_i} \ge 0,\ \ \forall z\in {\mathcal {Z}}^i,\ \forall i \in \mathcal {M}. \end{aligned}$$

(24)

Thus the reduced cost of each pricing problem in the final column generation iteration is

$$\begin{aligned} {\tilde{r}}_i:= \min \left\{ z_{m+1} - {{\hat{\gamma }}}^{\hat{\mathsf {T}}} z_{[m]} - {\hat{\alpha }_i}\; :\; z\in {\mathcal {Z}}^i\right\} \ge 0,\qquad \forall i \in \mathcal {M}. \end{aligned}$$

(25)

Furthermore, the LP relaxation of (IP-M) has objective value given by the optimal LP duals according to:

$$\begin{aligned} \nu ^{IP}_{LP} = b^{\hat{\mathsf {T}}} {{\hat{\gamma }}} + {\varvec{1}}^{\hat{\mathsf {T}}} {\hat{\alpha }_i}. \end{aligned}$$

(26)

Now consider the following relaxation for the LP relaxation of (LB-M) with the addition of the pricing cuts from the final column generation iteration:

$$\begin{aligned} \nu ^{LB}_{R} := \min \&\sum _{i \in \mathcal {M}}\left( \sum _{k=1}^{|{{\mathcal {P}}}^i|} {\lambda }^i_kz^{i,k}_{m+1} + \sum _{r=1}^{q_i} w^i_r \right) \end{aligned}$$

(27a)

$$\begin{aligned} \text {s.t.} \&\sum _{i \in \mathcal {M}}\left( \sum _{k=1}^{|{{\mathcal {P}}}^i|} {\lambda }^i_kz^{i,k}_{[m]} + \sum _{r=1}^{q_i} u^i_r\right) \le b\end{aligned}$$

(27b)

$$\begin{aligned}&\sum _{k=1}^{|{{\mathcal {P}}}^i|} {\lambda }^i_k+ \sum _{r=1}^{q_i} \mu ^i_r=1, \qquad \qquad&i \in \mathcal {M}\end{aligned}$$

(27c)

$$\begin{aligned}&w^i_r - {{\hat{\gamma }}}^\top u^i_r \ge ({\tilde{r}}_i+ {\hat{\alpha }_i}) \mu ^i_r,\qquad&i \in \mathcal {M}, \ r=1,\ldots ,q_i\end{aligned}$$

(27d)

$$\begin{aligned}&\lambda \ge {\varvec{0}},\ \mu \ge {\varvec{0}},\ w\ \text {free},\ u\ \text {free}.&\end{aligned}$$

(27e)

Using dual variables $\gamma \le {\varvec{0}}$ to denote the LP dual multipliers for constraint (27b), $\alpha$ (unrestricted in sign) to denote the vector of LP dual multipliers for the constraint (27c), and $\eta ^i_r\ge 0$ to denote the LP dual multipliers for each pricing cut in (27d) indexed by $i \in \mathcal {M}$, $r=1,\dots ,q_i$, we formulate the LP dual to the above LP:

$$\begin{aligned} \max \&b^T \gamma + {\varvec{1}}^T \alpha _i\end{aligned}$$

(28a)

$$\begin{aligned} \text {s.t.} \&\gamma ^{\mathsf {T}}z^{i,k}_{[m]} + \alpha _i\le z^{i,k}_{m+1},\qquad&i \in \mathcal {M},\ k=1,\dots ,|{{\mathcal {P}}}^i| \end{aligned}$$

(28b)

$$\begin{aligned}&\eta \le {\varvec{1}}\end{aligned}$$

(28c)

$$\begin{aligned}&\gamma - {\hat{\alpha }_i} \le {\varvec{0}}\end{aligned}$$

(28d)

$$\begin{aligned}&\alpha _i- ({\tilde{r}}_i+ {{\hat{\alpha }}_i})\eta ^i_r \le 0&i \in \mathcal {M},\ r=1,\ldots ,q_i\end{aligned}$$

(28e)

$$\begin{aligned}&\gamma \le {\varvec{0}},\ \alpha \ \text {free},\ \eta \ge {\varvec{0}}. \end{aligned}$$

(28f)

Setting $\gamma :={\hat{\gamma }}$, $\alpha :={\hat{\alpha }}$, $\eta :={\varvec{1}}$ yields a feasible solution to the above LP: (28b) follows from (24) and since $z^{i,k}\in {\mathcal {Z}}^i$ for all i, k; (28c) and (28d) follow immediately from the definitions of $\eta$ and $\gamma$; and (28e) follows from the definitions and from (25). By (26) and since $\gamma :={\hat{\gamma }}$, $\alpha :={\hat{\alpha }}$, $\eta :={\varvec{1}}$ yields a feasible solution to the above LP, which is dual to the relaxation of the LP relaxation of (LB-M), its objective value, which is ${\hat{\gamma }}^{\hat{\mathsf {T}}} b + {\hat{\alpha }}^{\hat{\mathsf {T}}} {\varvec{1}}$, satisfies

$$\begin{aligned} \nu ^{IP}_{LP} = {\hat{\gamma }}^{\hat{\mathsf {T}}} b + {\hat{\alpha }}^{\hat{\mathsf {T}}} {\varvec{1}}\le \nu ^{LB}_{R} \le \nu ^{LB}_{LP} \end{aligned}$$

and the result follows. $\square$

Initial region creation example

As an example of Algorithm 2, consider a case with three objectives where two NDPs, namely (4, 4, 4) and (1, 8, 1), are discovered for MOP$(i)$, which has supernal point (50, 50, 50). The regions created during Algorithm 2 (where $\epsilon = 1$) are shown in Fig. 6 in a tree. A region is represented by a triplet in brackets, where each component represents an upper bound on the corresponding objective, e.g., $\langle \delta _1,\delta _2,\delta _3\rangle$ defines the polyhedral region $\{ z\in {\mathbb {R}}^3 : z_j \le \delta _j, j=1,2,3 \ \}$. Level $\ell$ of the tree corresponds to the $\ell {\text {th}}$ iteration of the algorithm and therefore to the list of regions in that iteration. The boxed regions are the ones returned at the end of the fifth step of the algorithm. The shaded boxes represent redundant regions, which are contained in other regions, and can safely be removed in the last step of the algorithm.

Fig. 6

Algorithm 2 applied to MOP$(i)$ with supernal point (50, 50, 50), provided $\epsilon = 1$ and ${{\mathcal {P}}}^i= \{(4,4,4),(1,8,1) \}$

We note that the decomposition technique used in Algorithm 2 is the same as the so-called full m-split in [14] when all the initial lower and upper bounds are taken as negative infinity and the supernal point, respectively. In [14], the authors only generate hypercubes as the regions, which are called boxes. They point out that the decomposition algorithm based on full m-split typically creates nested, and hence, redundant, boxes. The authors analyze conditions under which redundant boxes occur, and suggest to detect and remove them from the decomposition immediately in every iteration. In the case illustrated in Fig. 6, as $(3,50,0) \le (50,50,0)$, the region represented by $\langle 3,50,0\rangle$ is redundant, as is the region represented by $\langle 0,50,3\rangle$, since $(0,50,3) \le (0,50,50)$. Note that the tree node corresponding to the region represented by $\langle 50,3,50\rangle$ has no descendants, since $(1,8,1)\not \le (50,3,50)$.

We also note that, in the case of a single coupling constraint, (i.e., $m=1$), redundancy does not occur, as any NDP belongs to exactly one of the regions on the list at any point in Algorithm 2.

Examples for branch-and-price comparison

1.1 Column generation

Example 1

Consider the following integer program with two identical blocks and a single linking constraint:

$$\begin{aligned}&\min \left\{ x^1_1+x^2_1 : x^1 \in {\mathcal {X}}^1, x^2 \in {\mathcal {X}}^2, x^1_2 + x^2_2 \le 3 \right\} , \ \text {where} \\&{\mathcal {X}}^1={\mathcal {X}}^2={\mathcal {X}}:= \left\{ x\in {\mathbb {Z}}^2 : 2x_1 + 3 x_2 \ge 6, 0 \le x_1, x_2 \le 3 \right\} . \end{aligned}$$

As shown in Fig. 7, for any block $i \in \{ 1,2 \}$, the set of NDPs for MOP$(i)$ is ${{\mathcal {N}}}^i= \{ (0,3), (1,2), (2,0) \}$, while the set of extreme points of the convex hull of its feasible set is ${{\mathcal {E}}}^i= \{ (0,2), (3,0), (0,3), (3,3) \}$. The IP has optimal value 2, with two, symmetric, optimal solutions: $x^1=(2,1)$, $x^2=(0,2)$ and $x^1=(0,2)$, $x^2=(2,1)$. Importantly, $(2,1)\in {\mathcal {X}}$ maps to the NDP (1, 2), and is required in an optimal solution, but (2, 1) is interior to $\text {conv}({\mathcal {X}})$.

Fig. 7

Feasible set of MOP$(i)$ subproblems, in decision space (${\mathcal {X}}^i$) and its convex hull ($\text {conv}({\mathcal {X}}^i)$) on the left, and in criterion space (${\mathcal {Z}}^i$) on the right

The MOP-based reformulation of this IP, (7), is

$$\begin{aligned} \min \left\{ \sum _{i=1,2} \left( 2{\lambda }^i_2 + 3{\lambda }^i_3\right) \; :\; \sum _{i=1,2} \left( 2{\lambda }^i_1 + {\lambda }^i_2\right) \le 3,\ {\lambda }^i_1 + {\lambda }^i_2 + {\lambda }^i_3=1,\ {\lambda }^i\in \{0,1\}^3,\ i=1,2 \right\} , \end{aligned}$$

which has two alternative optimal solutions: $\lambda ^1=(0,1,0)$, $\lambda ^2=(1,0,0)$ and $\lambda ^1=(1,0,0)$, $\lambda ^2=(0,1,0)$, corresponding to the two optimal solutions to the original IP, respectively.

By contrast, the Dantzig–Wolfe reformulation based on the convexification approach has LP master problem

$$\begin{aligned} \min&\left\{ \sum _{i=1,2} \Big (3{\lambda }^i_2 + 3{\lambda }^i_4\Big )\; :\; \sum _{i=1,2} \Big (2{\lambda }^i_1 + 3{\lambda }^i_3 + 3{\lambda }^i_4\Big ) \le 3, \right. \\&\left. \ {\lambda }^i_1 + {\lambda }^i_2 + {\lambda }^i_3+{\lambda }^i_4=1,\ {\lambda }^i\ge {\varvec{0}},\ i=1,2 \right\} . \end{aligned}$$

Treating this as an IP, by requiring ${\lambda }^i\in \{0,1\}^4$ for $i=1,2$, does not give a valid reformulation of the original IP. It has optimal value 3, given by, for example, $\lambda ^1=(1,0,0,0)$ and $\lambda ^2=(0,1,0,0)$. Instead, solving the LP master problem gives optimal value 1.5, with (one possible) solution $\lambda ^1=(1,0,0,0)$ and $\lambda ^2=(0.5,0.5,0,0)$, corresponding to $x^1=(0,2)$, $x^2=(1.5,1)$. Branching on $x^2_1$ gives two new IPs: on one branch, $x^2_1\le 1$ is applied, while on the other, $x^2_1 \ge 2$ is applied. On this latter branch, ${\mathcal {E}}^2 = \{(2,1),(3,0),(2,3),(3,3)\}$, and the solution $x^2=(2,1)$ is now “exposed”: the optimal solution to the Dantzig-Wolfe LP master problem at this node of the branch-and-price tree is that corresponding to $x^1=(0,2)$, $x^2=(2,1)$, an optimal solution to the original IP. However the former branch, with ${\mathcal {E}}^2 = \{(0,2),(1,2),(0,3),(1,3)\}$, returns LP master solution corresponding to $x^1=(1.5,1)$, $x^2=(0,2)$, the LP solution symmetric to that at the root node. Thus this branch needs to be explored further before optimality can be proved.

Example 2

Consider the following integer program with $M$ identical blocks, each corresponding to an assignment problem, and a single linking constraint:

$$\begin{aligned}&\min \Big \{ \sum _{i \in \mathcal {M}} x^i_{11} : \ x^i\in {\mathcal {X}}_{AP}, \, i \in \mathcal {M}\ \text {and} \ \sum _{i \in \mathcal {M}} x^i_{22} \le M\Big \}, \ \text {where} \\&\quad {\mathcal {X}}_{AP} = \Big \{ x\in \{ 0,1 \}^{n \times n} : \sum _{h=1}^n x_{h \ell } = 1, \ell =1,\ldots ,n, \ \sum _{\ell =1}^n x_{h \ell } = 1, h=1,\ldots ,n \Big \}. \end{aligned}$$

Note that the linking constraint is indeed redundant as $x$ variables are all binary. For $i \in \mathcal {M}$, we have

$$\begin{aligned} \text {MOP(i)} : \min \{ x_{22}, x_{11} \} \ \text {s.t.} \ x\in {\mathcal {X}}_{AP} \ \Rightarrow \ {{\mathcal {N}}}^i= \{ (0,0) \}, \end{aligned}$$

thus (IP-M) consists of only $M$ columns. On the other hand, the extreme points of the assignment polytope (also known as the Birkhoff polytope) correspond to 0-1 matrices of size $n \times n$ with exactly one 1 on every row and every column. Under the objective of MOP$(i)$ subproblem, these n! extreme points yield $2^2$ different images (all binary permutations of size two), which means that the Dantzig–Wolfe reformulation of the problem has $4M$ columns in total. Therefore, the difference between the number of columns in two formulations becomes larger as the number of blocks increases. Lastly, we note that the difference can be made even larger by adding more linking constraints.

$\Box$

Example 3

Consider the following integer program with two identical blocks and a single linking constraint:

$$\begin{aligned}&\min \Big \{ x^1_2+x^2_2 : x^1 \in {\mathcal {X}}, x^2 \in {\mathcal {X}}, x^1_1 + x^2_1 \le 3 \Big \}, \ \text {where} \\&\quad {\mathcal {X}}= \Big \{ x\in {\mathbb {Z}}^2 : x_1 + 2 x_2 \ge 7, \ 0 \le x_1, x_2 \le 4 \Big \}. \end{aligned}$$

For any block $i \in \{ 1,2 \}$, we have ${{\mathcal {N}}}^i= \{ (0,4), (1,3), (3,2) \}$. Suppose that we initialize the LP relaxation (in Step 1) with dummy columns corresponding to ideal point $z^I= (0,2)$ with sufficiently big objective coefficients, e.g., 100. Then, at the very first iteration of the standard column generation, as the optimal dual multiplier of the linking constraint happens to be zero, both (3, 2) and (4, 2) are the columns with the most negative reduced cost. Therefore, we might be adding the column (4, 2) which is weakly nondominated. $\square$

1.2 Branching

Example 4

We consider a problem, with a single linking constraint, of the form

$$\begin{aligned} \min \left\{ \sum _{i=1}^2 (c^i)^\top x^i: \ x^i\in {\mathcal {X}}_{AP}, \, i=1,2 \ \text {and} \ \sum _{i=1}^2 A^i x^i\le b \right\} , \end{aligned}$$

where

$$\begin{aligned} {\mathcal {X}}_{AP} = \left\{ x\in \{ 0,1 \}^{n \times n} : \sum _{h=1}^n x_{h \ell } = 1, \ell =1,\ldots ,n, \ \sum _{\ell =1}^n x_{h \ell } = 1, h=1,\ldots ,n \right\} . \end{aligned}$$

We generate an instance with $n=10$ by letting the entries of $c^i$ and $A^i$ for $i=1,2$ to be integers drawn uniformly from $\{ 0,\ldots ,40 \}$. We set $b=200$. The data for the resulting instance is given below, with matrix data given with rows concatenated. So, for example, $c^1_{3,7}=6$ is given by the 27th entry in the $c^1$ vector.

$A^1 =$ [3, 3, 4, 19, 1, 21, 10, 36, 17, 32, 34, 36, 3, 19, 8, 34, 30, 0, 5, 23, 19, 5, 32, 40, 2, 13, 4, 20, 31, 12, 15, 36, 17, 19, 14, 19, 40, 24, 14, 19, 17, 9, 14, 23, 28, 25, 16, 17, 27, 23, 1, 5, 28, 33, 5, 33, 8, 11, 12, 0, 23, 27, 36, 0, 5, 9, 21, 7, 35, 37, 26, 13, 6, 1, 36, 34, 26, 14, 11, 12, 37, 14, 20, 27, 9, 25, 19, 17, 38, 33, 17, 20, 20, 12, 22, 27, 23, 4, 36, 17]

$c^1 =$ [33, 20, 25, 23, 8, 13, 32, 4, 14, 13, 8, 11, 11, 22, 33, 5, 23, 18, 19, 24, 21, 40, 0, 28, 4, 23, 6, 4, 2, 4, 20, 37, 26, 4, 20, 34, 19, 13, 38, 33, 26, 5, 3, 37, 30, 38, 3, 12, 15, 22, 38, 37, 23, 39, 26, 28, 23, 32, 34, 25, 36, 13, 22, 21, 17, 3, 16, 38, 16, 13, 30, 3, 21, 35, 1, 10, 32, 4, 24, 8, 29, 23, 6, 11, 23, 33, 39, 5, 24, 34, 31, 22, 6, 14, 4, 25, 17, 21, 22, 33]

$A^2 =$ [27, 12, 32, 32, 21, 8, 23, 29, 22, 7, 12, 3, 40, 39, 19, 28, 33, 18, 17, 36, 18, 4, 21, 5, 29, 29, 9, 20, 0, 31, 10, 27, 2, 3, 18, 25, 14, 3, 13, 36, 12, 28, 0, 14, 26, 19, 3, 18, 40, 22, 15, 17, 27, 39, 23, 17, 27, 34, 38, 27, 26, 9, 13, 31, 14, 33, 15, 30, 38, 31, 25, 12, 18, 28, 26, 5, 8, 31, 25, 7, 13, 2, 27, 40, 0, 9, 18, 29, 4, 17, 15, 31, 28, 30, 23, 2, 24, 38, 34, 22]

$c^2 =$ [30, 8, 17, 2, 11, 2, 30, 27, 30, 11, 9, 23, 6, 37, 9, 0, 15, 28, 39, 12, 30, 18, 10, 24, 7, 39, 21, 40, 29, 31, 16, 21, 0, 35, 23, 11, 37, 12, 40, 28, 25, 8, 10, 31, 7, 21, 31, 22, 9, 31, 36, 0, 10, 8, 24, 19, 6, 4, 20, 38, 38, 37, 18, 38, 33, 0, 9, 32, 14, 10, 19, 0, 21, 32, 31, 28, 12, 23, 11, 21, 15, 7, 22, 27, 15, 5, 5, 23, 12, 25, 20, 11, 23, 38, 8, 16, 40, 19, 7, 15]

$b = 200$

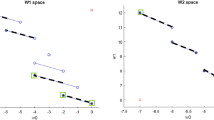
For this instance, the NDFs of MOP subproblems are given in Fig. 8. The circle points in the figure correspond to the columns generated at Step 1 of Algorithm 1, i.e., when the LP relaxation of (IP-M) is solved. We note that these columns are also the images of the columns generated when the LP relaxation of the Dantzig–Wolfe reformulation is solved via column generation, since the initial steps of the classical branch-and-price and our MOP-based branch-and-price coincide. Lastly, the circle points with a cross in the figure represent the NDPs whose corresponding columns have a positive weight in the optimal LP solution.

Fig. 8

NDF of MOP$(i)$ subproblems which are biobjective assignment problems (${\mathcal {N}}^1$ on the left, ${\mathcal {N}}^2$ on the right)

Only the LP relaxation for block $i=2$ is fractional: there is positive weight on the NDPs (94, 107) and (119, 92), while for block $i=1$, the NDP (90, 106) is selected.

For this instance, the (not quite complete) branch-and-bound tree obtained by using the traditional column generation branching and the branch-and-bound tree obtained using the new NDP-based branching rule are provided below. In both cases, we use the best bound search strategy, since this is guaranteed to give the smallest tree.

Traditional column generation branching would branch on a fractional $x^i_{h \ell }$ variable. On one branch, all columns corresponding to solutions with $x^i_{h \ell }=1$ are removed and $x^i_{h \ell }$ is fixed to 0 fixed in the column generation subproblem for i, which does not change its assignment problem structure. On the other branch, all columns corresponding to solutions with $x^i_{h \ell }=0$ are removed and $x^i_{h \ell }$ is fixed to 1 fixed in the column generation subproblem, which again preserves its assignment problem structure. There could very well be many possible $i, h, \ell$ indices, and there seems to be little to guide which to choose. Also, changing just one variable in the assignment subproblems may not have a big effect, if there are many alternative assignment solutions with fairly similar resource consumption and cost values, which can occur if the problem exhibits symmetry or near-symmetry. Solving this instance using the standard approach of selecting the branching variable $x^i_{h \ell }$ to be that which is most fractional in the LP solution, breaking ties by choosing the variable with the smallest index in terms of the lexicographical order of $i,h,\ell$, we obtain the incomplete branch-and-bound tree given in Fig. 9. Note the tree has 103 nodes, with an optimal solution first found at depth 11, but has one node that still needs to be explored. During the whole search, at least 201 different columns from the ${\mathcal {Z}}^i$ sets are generated.

Fig. 9

The branch-and-bound tree obtained by using the traditional column generation branching rule and the best-first search strategy. Left (right) branch corresponds to fixing a decision variable to zero (one)

Several branches in this tree have subproblem feasible regions that contain no NDPs. For instance, such a case occurs at a node at depth three, after fixing $x^2_{1,6}=0,x^2_{6,2}=1,x^2_{2,1}=0$, in that order. These branching constraint restrict the feasible set of MOP(2) to a region containing no NDPs. However, this branch has master LP objective value 216.8, and so is pruned once the optimal solution is discovered, having value 209. Another example is seen at depth seven, at the node obtained after fixing $x^2_{1,6} = 1, x^1_{3,7} = 0, x^1_{1,2} = 0, x^1_{1,1} = 0, x^1_{1,3} = 0, x^1_{1,5} = 0, x^1_{4,1} = 1$ in that order. Here, the feasible set of MOP(1) contains no NDPs. This node has LP objective value 207.9, and so needs to be explored before optimality is confirmed.

By contrast, consider NDP-based branching. Let ${\lambda }^i_k$ be fractional in the optimal LP solution. Then, there must exist $k' \ne k$ with $\lambda ^i_{k'}$ also fractional and at least one index j for which $z^{i,k}_j\ne z^{i,k'}_j$. Here we preference the choice of $j=m+1=2$, which denotes the objective component, since it is most likely to increase the lower bound quickly. In this case, the NDP-based branch rule produces two branches (as $m=1$) via the disjunction

$$\begin{aligned} { A^i x^i\le z^{i,k}_1 - \epsilon \ \ \ \bigvee \ \ \ (c^i)^\top x^i\le z^{i,k}_2} \end{aligned}$$

where $\epsilon =1$ can be used for pure IPs and k is the index of the fractionally selected NDP for MOP$(i)$ having smallest objective value. For example, at the root node of the instance, $i=2$ is chosen, as both (94, 107) and (119, 92) are selected fractionally in the LP relaxation. Since the latter has smaller objective value, it is used to create the branching disjunction, which is thus

$$\begin{aligned} { A^2 x^2 \le 118 \ \ \ \bigvee \ \ \ (c^2)^\top x^2 \le 92}. \end{aligned}$$

This branching rule is implemented by adding one of the branching constraints to MOP$(i)$, removing the columns violating this constraint from the master LP, and re-solving the master LP to optimality, where more NDPs are possibly generated.

The full branch-and-bound tree obtained for this instance, given in Fig. 10, has only 11 nodes in total, four of which are pruned by infeasibility. In total, 17 different columns from the ${\mathcal {N}}^i$ sets are generated. The optimal solution is found at depth four. In Fig. 10, boxes with solid borders represent integral LP solutions, whereas boxes with dashed borders represent fractional LP solutions, where the corresponding NDPs for $i=1$ and $i=2$ are given in the left and right columns, respectively, and the optimal value is denoted by “obj”. The optimal solution appears in the shaded box, at depth four. Constraints added to the MOP subproblems are given on the arrows, where $z^i_1 := A^i x$ and $z^i_2 := (c^i)^\top x$ are used for convenience.

Fig. 10

The branch-and-bound tree obtained by using the new NDP-based branching rule and the best-first (also known as best bound) tree search strategy

Computational results

1.1 Redundancy check

We examine the effect of detecting and removing redundant regions. Specifically, for KC and MMKP instances, we turn off the redundancy check in the algorithm setting found to be best overall: no pricing cuts, $\beta ={\varvec{1}}$ throughout and the Conservative region refinement strategy. In Table 3, the total CPU time (in s) and the number (LB-M) iterations to solve an instance are given in the columns labeled as “Time” and “It”, respectively. The (geometric for KC, arithmetic for MMKP) average, over $M$ blocks, of the initial number of regions, i.e., the number of regions obtained at the end of Step 2 of Algorithm 1, and of the total number of regions generated throughout the algorithm are provided in the columns labeled as “Init” and “Tot”, respectively. Lastly, the (geometric for KC, arithmetic for MMKP) average number of redundant regions detected and removed at Step 2 and Step 3 are given in the last two columns labeled as “St2” and “St3”, respectively.

Table 3 Redundancy check results for KC instances, and small MMKP instances with $|{\mathcal {K}}| = 3$ (Setting: No pricing cuts, $\beta = {\varvec{1}}$, conservative region refinement)

For KC, we observe that when redundant regions are removed, (LB-M) is initialized with almost half as many regions, the total number of generated regions is reduced by an order of magnitude, and accordingly the algorithm converges in a significantly smaller number of iterations, and so is much faster. Moreover, the average time spent on detecting redundant regions is only 0.002 s per instance. Lastly, we note that the number of initial regions in the case with redundancy check plus the number of redundant regions removed at Step 2 is not necessarily equal to the number of initial regions in the case without redundancy check, as redundant regions are removed at the end of each refinement step.

For the easiest MMKP instances, although the solution times are still small in the absence of the redundancy check, they are roughly doubled. The redundancy check times are again negligible, constituting almost always less than 1%, and at most 1.25%, of the solution times for those small instances. More importantly, without detecting and removing redundant regions, none of the large MMKP instances, INST13–INST20, can be solved in the time limit of an hour.

We also illustrate the impact of the redundancy check in a different algorithmic setting in Table 4 for the KC instances. In this version of the algorithm, where we apply both the pricing cuts and the aggressive region refinement, we observe that when redundant regions are removed, (LB-M) is initialized with almost half as many regions, the total number of generated regions is reduced by an order of magnitude, and accordingly the algorithm converges in a significantly smaller number of iterations, and so is much faster. Moreover, the average time spent on detecting redundant regions is only 0.0003 s per instance.

Table 4 Additional redundancy check results for KC instances (Setting: Pricing cuts, $\beta$ guided by (LB-M) while switching to the vector of ones as needed, aggressive region refinement)

In summary, we observe that redundancy check times are negligible, and that when redundant regions are removed, (LB-M) is initialized with a significantly smaller number of regions, the total number of generated regions is reduced by an order of magnitude, and accordingly the algorithm converges much faster. Without the redundancy check, none of the large MMKP instances can be solved in the time limit. Lastly, the impact of redundancy check is magnified if a more aggressive region refinement strategy is used. We conclude that removing redundant regions plays a crucial role in attaining efficiency.

1.2 Algorithmic choices

Solution times are reported in s (or “TL” standing for time limit). Best times are indicated in bold font.

Table 5 Time comparison of alternative settings for KC instances, and small MMKP instances with $|{\mathcal {K}}| = 3$

Results for small MMKP instances with more linking constraints, without the use of pricing cuts, are provided in Table 6, where the best CPU times are displayed in bold. While the $\beta$ selection strategy comparison remains the same as in Table 5, the region refinement domination result is reversed: the Conservative strategy reduces solution times by 32% on the average. More specifically, we find that in MMKP instances, the duals obtained from (LB-M) always include a zero element, and the alternatives for $\beta$ that we consider in this case almost always lead to the discovery of the same NDPs, and thus do not change the course of the algorithm. On the other hand, the Conservative refinement strategy doubles the number of iterations but yields time savings (Table 6).

Table 6 Time comparison of alternative settings for small MMKP instances with $|{\mathcal {K}}| = 5$ (Setting: No pricing cuts)

Table 7 $\beta$ vector selection results for KC instances (Setting: Pricing cuts, aggressive region refinement)

1.3 $\varvec{\beta }$ vector selection

In Table 7, we provide additional, more detailed, results for the KC instances, to provide insights into the trade-offs in play for alternative choices of $\beta$ in the setting with pricing cuts and the Aggressive region refinement strategy. In addition to the solution times (“Time” columns) and the number of (LB-M) iterations (“It” columns), we provide the average number of times Line 16 is executed in Algorithm 3 (St16 columns) and the number of iterations performed in Algorithm 3 (“It2” columns) per (LB-M) iteration. Also, for the fallback option when $\beta$ is supplied by the (LB-M)duals, we give the number of times we switch to $\beta = {\varvec{1}}$ in the last column of the table.

From these results, we see that the algorithm gets into Line 16 less frequently, which in turn yields reductions in the number of (LB-M) iterations, in most instances, and in the number of iterations performed in Algorithm 3. However, these do not always translate into reductions in overall solution times, which are still lower for the hardest instances when using the constant $\beta ={\varvec{1}}$ option.

1.4 Aggressive versus conservative refinement

In Table 8, we provide total solution time (Time), the number (LB-M) iterations (It); and the (geometric) average, over all blocks, of the number of regions obtained at the end of Step 2 (Init), and of the total number of regions generated throughout the algorithm (Tot).

Table 8 Refinement results for small MMKP instances with $|{\mathcal {K}}|=5$ (Setting: No pricing cuts, $\beta = {\varvec{1}}$)