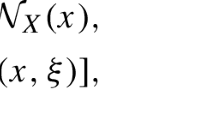Distributionally robust stochastic variational inequalities

Abstract

We propose a formulation of the distributionally robust variational inequality (DRVI) to deal with uncertainties of distributions of the involved random variables in variational inequalities. Examples of the DRVI are provided, including the optimality conditions for distributionally robust optimization and distributionally robust games (DRG). The existence of solutions and monotonicity of the DRVI are discussed. Moreover, we propose a sample average approximation (SAA) approach to the DRVI and study its convergence properties. Numerical examples of DRG are presented to illustrate solutions of the DRVI and convergence properties of the SAA approach.

7 Appendix

In this Appendix, we give some proofs and necessary results used in this paper.

Example 8

Consider the Average Value-at-Risk,

$$\begin{aligned} \mathsf{AV@R}_{1-\alpha }(Z)&:= \frac{1}{1-\alpha }\int _{\alpha }^1 H_Z^{-1}(t) dt\nonumber \\&= \inf _{\tau \in {\mathbb {R}}}\left\{ \tau +(1-\alpha )^{-1}{\mathbb {E}}_{\mathbb {P}}[Z-\tau ]_+\right\} , \;\alpha \in (0,1). \end{aligned}$$

(A1)

Here ${{\mathcal {Z}}}=L_1(\Xi ,{{\mathcal {B}}},{\mathbb {P}})$ and a minimizer in the right hand side of (A1) is ${\bar{\tau }}=H_Z^{-1}(\alpha )$. The empirical estimate of $\mathsf{AV@R}_{1-\alpha }(\phi ^x)$ is then

$$\begin{aligned} {\widehat{\mathsf{AV@R}}}_{(1-\alpha ) N}(\phi ^x) = \inf _{\tau \in {\mathbb {R}}}\left\{ \tau +\frac{1}{(1-\alpha ) N}\sum _{j=1}^N\left[ \phi ^x(\xi ^j)-\tau \right] _+\right\} . \end{aligned}$$

(A2)

We have that $\partial \mathsf{AV@R}_{1-\alpha }(Z)$ is a singleton iff ${\mathbb {P}}\{Z=\kappa \}=0$, where $\kappa _\alpha :=H_Z^{-1}(\alpha )$. Suppose that $\partial \mathsf{AV@R}_{1-\alpha }(Z)=\{{\bar{\zeta }}\}$ is a singleton. Then

$$\begin{aligned} {\bar{\zeta }}(s)=\left\{ \begin{array}{cll} (1-\alpha )^{-1}&{}if &{} Z(s)>\kappa ,\;s\in \Xi ,\\ 0 &{}if &{} Z(s)<\kappa ,\;s\in \Xi , \end{array}\right. \end{aligned}$$

(A3)

(cf. [27, eq. (6.80), p. 292]). For $x\in X$ and $Z:=\phi ^x$ let $\{{\bar{\zeta }}^x\}$ be the corresponding subdifferential. The subdifferential ${\hat{\zeta }}^x=(\zeta ^x_1,\ldots ,\zeta ^x_N)$ of the corresponding empirical estimate is obtained by replacing $\kappa _\alpha$ with their empirical estimates. That is $\zeta ^x_j=(1-\alpha )^{-1}$ if $\phi ^x(\xi ^j)> \kappa _{\alpha , N}$ and $\zeta ^x_j=0$ if $\phi ^x(\xi ^j)<\kappa _{\alpha ,N}$, where $\kappa _{\alpha ,N}$ is the empirical estimate of $\kappa _\alpha$. Note that because of the assumption ${\mathbb {P}}\{Z=\kappa \}=0$, the empirical estimate $\kappa _{\alpha ,N}$ converges w.p.1 to $\kappa _\alpha$.

Consider the probability distribution $P^x_{N}$ on $\{\xi ^1,\ldots ,\xi ^N\}$ associated with density ${\hat{\zeta }}^x$, i.e., with $\xi ^j$ being assigned probability $1/((1-\alpha ) N)$ if $\phi ^x(\xi ^j)>\kappa _{\alpha ,N}^x$, and 0 otherwise. We view $P^x_{N}$ as the empirical counterpart of $P^x$, where $P^x$ is the probability measure absolutely continuous with respect to ${\mathbb {P}}$ and having density ${\bar{\zeta }}^x$, i.e.,

$$\begin{aligned} dP^x={\bar{\zeta }}^x d{\mathbb {P}}. \end{aligned}$$

(A4)

Consider a continuous bounded function $g:\Xi \rightarrow {\mathbb {R}}$. Since $g(\cdot )$ is bounded and continuous, $\kappa _{\alpha ,N}^x\rightarrow \kappa _\alpha ^x$ w.p.1 and ${\mathbb {P}}\{\phi ^x(\xi )=\kappa _\alpha ^x\}=0$, we have that

$$\begin{aligned} \int _\Xi g(s) dP^x_{N}(s)=\frac{1}{(1-\alpha ) N}\sum _{\phi ^x(\xi ^j)>\kappa _{\alpha ,N}^x} g(\xi ^j) \end{aligned}$$

converges w.p.1 to

$$\begin{aligned} \int _\Xi g(s){\bar{\zeta }}^x(s)d{\mathbb {P}}(s)=\frac{1}{1-\alpha }\int _{\phi ^x(\xi )>\kappa _{\alpha }^x} g(s)d{\mathbb {P}}(s). \end{aligned}$$

That is $P^x_{N}$ converges weakly¹¹ to $P^x$. Moreover, by Proposition 6 in the Appendix, we have if $\{x_N\}$ is a sequence in X converging to x, then $\int _\Xi g(s) dP^{x_N}_{N}(s)$ converges to $\int _{\phi ^x(\xi )>\kappa } g(s)d{\mathbb {P}}(s)$ w.p.1, and hence $P^{x_N}_{ N}$ converges weakly to $P^x$.

Proposition 6

Suppose (i) $\phi (\cdot ,\xi )$ is Lipschitz continuous in $x\in X$ with a uniform Lipschitz modules $k_\phi$, (ii) the CDF of $\phi ^{{\bar{x}}}$ is strictly monotone, and (iii) $\{x_N\}$ is a sequence in X converging to ${\bar{x}}$, (iv) $|\kappa ^{x'}_\alpha |$ is bounded by a constant number for all $x'\in {{\mathcal {B}}}(x)\cap X$. Then for any bounded and continuous function g, $\int _\Xi g(s) dP^{x_N}_{N}(s)$ converges to $\int _{\phi ^{{\bar{x}}}(\xi )>\kappa _{\alpha }^{{\bar{x}}}} g(s)d{\mathbb {P}}(s)$.

Proof

For any continuous and bounded function g(s),

$$\begin{aligned} \begin{array}{lll} &{}&{}\left| \displaystyle {\frac{1}{\alpha N}\sum _{\phi ^{x_N}(\xi ^j)>\kappa ^{x_N}_{\alpha ,N}} g(\xi ^j) - \frac{1}{\alpha }\int _{\phi ^{{\bar{x}}}(\xi )>\kappa _{\alpha }^{{\bar{x}}}} g(s)d{\mathbb {P}}(s)} \right| \\ &{}&{}\quad \le \left| \displaystyle {\frac{1}{\alpha N}\sum _{\phi ^{x_N}(\xi ^j)>\kappa ^{x_N}_{\alpha ,N}} g(\xi ^j) - \frac{1}{\alpha N}\sum _{\phi ^{{{\bar{x}}}}(\xi ^j)>\kappa ^{{\bar{x}}}_{\alpha }} g(\xi ^j)} \right| \\ &{}&{}\quad + \left| \displaystyle {\frac{1}{\alpha N}\sum _{\phi ^{{{\bar{x}}}}(\xi ^j)>\kappa ^{{\bar{x}}}_{\alpha }} g(\xi ^j) - \frac{1}{\alpha }\int _{\phi ^{{{\bar{x}}}}(\xi )>\kappa _{\alpha }^{{\bar{x}}}} g(s)d{\mathbb {P}}(s)} \right| . \end{array} \end{aligned}$$

(A5)

We first prove that $\kappa _{\alpha ,N}^{x_N}$ converges to $\kappa _{\alpha }^{{\bar{x}}}$ w.p.1. To see this, by condition (ii), we have ${\mathbb {P}}\{\phi ^{{\bar{x}}}(\xi )=\kappa _{\alpha }^{{\bar{x}}}\}=0$, then

$$\begin{aligned} \kappa _{\alpha }^{{\bar{x}}} = \arg \min _\tau \; \tau + \frac{1}{1-\alpha }{\mathbb {E}}_{{\mathbb {P}}}\Big [\Big (\phi ^{{\bar{x}}} -\tau \Big )_+\Big ] \end{aligned}$$

and

$$\begin{aligned} \kappa _{\alpha ,N}^{x_N} \in \arg \min _\tau \; \tau + \frac{1}{(1-\alpha )N}\sum _{j=1}^N(\phi ^{x_N}(\xi ^j) -\tau )_+. \end{aligned}$$

It is easy to observe that $(\phi ^{{\bar{x}}}(\xi ) -\tau )_+$ is continuous w.r.t. x and dominated by an integrable function, then by uniform law of large numbers [27, Theorem 7.48]

$$\begin{aligned} \left| {\mathbb {E}}_{{\mathbb {P}}}[(\phi ^{{\bar{x}}} -\tau )_+] - \frac{1}{N}\sum _{j=1}^N(\phi ^{x_N}(\xi ^j) -\tau )_+\right| \rightarrow 0 \end{aligned}$$

as $N\rightarrow \infty$ w.p.1. Then by conditions (i)–(iv) and [5, Proposition 4.4], we have that $\kappa _{\alpha ,N}^{x_N}$ converges to $\kappa _{\alpha }^{{\bar{x}}}$ w.p.1.

Then we prove the convergence of first part in the right side of (A5). Let

$$\begin{aligned}&A^1_N=\{\xi \in \Xi : \phi ^{x_N}(\xi )>\kappa _{\alpha , N}^{x_N}, \phi ^{{\bar{x}}}(\xi )\le \kappa _\alpha ^{{\bar{x}}}\},\\&A^2_N=\{\xi \in \Xi : \phi ^{x_N}(\xi )\le \kappa _{\alpha , N}^{x_N}, \phi ^{{\bar{x}}}(\xi )> \kappa _\alpha ^{{\bar{x}}}\},\\&A^3_N=\{\xi \in \Xi : \phi ^{{\bar{x}}}(\xi )\ge \kappa _{\alpha , N}^{x_N}-k_\phi \Vert {\bar{x}}-x_N\Vert , \phi ^{{\bar{x}}}(\xi )\le \kappa _\alpha ^{{\bar{x}}}\} \end{aligned}$$

and

$$\begin{aligned} A^4_N=\{\xi \in \Xi : \phi ^{{\bar{x}}}(\xi )\le \kappa _{\alpha , N}^{x_N}+k_\phi \Vert {{\bar{x}}}-x_N\Vert , \phi ^{{\bar{x}}}(\xi )\ge \kappa _\alpha ^{{\bar{x}}}\}. \end{aligned}$$

Then

$$\begin{aligned} \begin{array}{lll} \left| \displaystyle {\frac{1}{\alpha N}\sum _{\phi ^{x_N}(\xi ^j)>\kappa ^{x_N}_{\alpha ,N}} g(\xi ^j) - \frac{1}{\alpha N}\sum _{\phi ^{{{\bar{x}}}}(\xi ^j)>\kappa ^{{\bar{x}}}_{\alpha }} g(\xi ^j)} \right| &{}\le &{} \frac{1}{\alpha }{\mathbb {P}}_N(A^1_N\cup A^2_N)|\max _sg(s)|\\ &{}\le &{} \frac{1}{\alpha }{\mathbb {P}}_N(A^3_N\cup A^4_N) |\max _sg(s)|, \end{array} \end{aligned}$$

where ${\mathbb {P}}_N$ is an empirical estimation of ${\mathbb {P}}$. Note that $\kappa ^{x_N}_{\alpha ,N}\rightarrow \kappa ^{{\bar{x}}}_\alpha$ and $x_N\rightarrow {\bar{x}}$, $A^1_N\subset A^3_N$ and $A^2_N\subset A^4_N$, and $A^3_N$ and $A^4_N$ converge to singleton sets. Then by condition (i) and (ii), ${\mathbb {P}}_N(A^1_N\cup A^2_N)\le {\mathbb {P}}_N(A^3_N\cup A^4_N) \rightarrow 0$ as $N\rightarrow \infty$ w.p.1, which implies

$$\begin{aligned} \begin{array}{lll} \left| \displaystyle {\frac{1}{\alpha N}\sum _{\phi ^{x_N}(\xi ^j)>\kappa ^{x_N}_{\alpha ,N}} g(\xi ^j) - \frac{1}{\alpha N}\sum _{\phi ^{x_N}(\xi ^j)>\kappa ^{{\bar{x}}}_{\alpha }} g(\xi ^j)} \right| \rightarrow 0 \end{array} \end{aligned}$$

(A6)

as $N\rightarrow \infty$ w.p.1.

Then we consider the second part in the right side of (A5). Since g is continuous and bounded, by classical law of large numbers, as $N\rightarrow \infty$ w.p.1,

$$\begin{aligned} \left| \displaystyle {\frac{1}{\alpha N}\sum _{\phi ^{{\bar{x}}}(\xi ^j)>\kappa ^{{\bar{x}}}_{\alpha }} g(\xi ^j) - \frac{1}{\alpha }\int _{\phi ^{{\bar{x}}}(\xi )>\kappa _{\alpha }^{{\bar{x}}}} g(s)d{\mathbb {P}}(s)} \right| \rightarrow 0. \end{aligned}$$

Combining discussion above, we have the conclusion. $\square$

Then we derive a kind of uniform Glivenko-Cantelli theorem which we need in the proof of Lemma 2. Let $f(x,\xi )$ be a random function and $\{x_N\}\rightarrow x$ as $N\rightarrow \infty$. Moreover, suppose $f(x, \xi )$ is Lipschitz continuous w.r.t. x and $\xi$, and the Lipschitz modules $\kappa (\xi )$ of $f(\cdot , \xi )$ is integrable. We use $H_{x_N}(t)$ and $H_{x}(t)$ to denote the CDF of $f(x_N, \xi )$ and $f(x, \xi )$ w.r.t. ${\mathbb {P}}$ and $H^N_{x_N}(t)$ and $H^N_{x}(t)$ are used to denote the CDF of their empirical distributions i.i.d samples $\{\xi ^1, \ldots , \xi ^N\}$.

Lemma 3

Suppose $f(x, \xi )$ is integrable and continuous w.r.t. x, and ${\mathbb {P}}$ is a continuous distribution. Then for each $\epsilon >0$, there exists a finite partition of the real line of the form $-\infty =t_0<t_1<\cdots <t_k=\infty$ such that for $0\le j\le k-1$, $H(x_N, t_{j+1}) - H(x_N, t_j)\le \epsilon$ for all N sufficiently large.

Proof

Since ${\mathbb {P}}$ is a continuous distribution, $H_{x}(t)$ is a CDF of continuous distribution and then, for any $\epsilon >0$ there exists $-\infty =t_0<t_1<\cdots <t_k=\infty$ such that for $0\le j\le k-1$, $H_x(t_{j+1}) - H_x(t_j)\le \frac{\epsilon }{2}$. Moreover, since $f(x, \xi )$ is integrable and continuous w.r.t. x, by Lebesgue’s dominated convergence theorem, for any continuous and bounded function h,

$$\begin{aligned} \lim _{N\rightarrow \infty }{\mathbb {E}}[h(f(x,\xi )) - h(f(x_N, \xi ))] = {\mathbb {E}}\left[ \lim _{N\rightarrow \infty }(h(f(x,\xi )) - h(f(x_N, \xi )))\right] =0. \end{aligned}$$

Then $f(x, \cdot )$ converges to $f(x_N, \cdot )$ weakly, which is equivalent to $\lim _{N\rightarrow \infty }|H_{x_N}(t) - H_{x}(t)|=0$ for any $t\in {\mathbb {R}}$. Then there exists sufficiently large N such that $\sup _{j\in \{0, \ldots , k\}}|H_{x_N}(t_j) - H_x(t_j)|\le \frac{\epsilon }{4}$. Then we have

$$\begin{aligned} \begin{array}{lll} |H_{x_N}(t_{j+1}) - H_{x_N}(t_j)|&{}\le &{} |H_{x_N}(t_{j+1}) - H_x(t_{j+1})| \\ &{}&{}+ |H_x(t_{j+1}) - H_x(t_j)|+ |H_x(t_{j}) - H_{x_N}(t_j)|\\ &{}\le &{} \frac{\epsilon }{4} + \frac{\epsilon }{2} + \frac{\epsilon }{4} = \epsilon . \end{array} \end{aligned}$$

$\square$

Theorem 3

Suppose $f(x, \xi )$ is Lipschitz continuous w.r.t. x and $\xi$, and the Lipschitz modules $\kappa (\xi )$ of $f(\cdot , \xi )$ is integrable, $f(x, \cdot )\in {{\mathcal {L}}}_P(\Xi , {{\mathcal {F}}}, {\mathbb {P}})$ and ${\mathbb {P}}$ is a continuous distribution. Then w.p.1

$$\begin{aligned} \lim _{N\rightarrow \infty }\sup _{t\in {\mathbb {R}}} |H^N_{x_N}(t) - H_{x}(t)| = 0, \end{aligned}$$

(A7)

and $(H^N_{x_N})^{-1}$ converges w.p.1 to $H_{x}^{-1}$ in the norm topology of ${{\mathcal {L}}}_p$ as $N\rightarrow \infty$.

Proof

Note that

$$\begin{aligned} |H^N_{x_N}(t) - H_{x}(t)|\le |H^N_{x_N}(t) - H_{x_N}(t)| + |H_{x_N}(t) - H_{x}(t)|. \end{aligned}$$

It is sufficient to show that for any $\epsilon >0$,

$$\begin{aligned} \limsup _{N\rightarrow \infty } \sup _t |H^N_{x_N}(t) - H_{x_N}(t)|\le \epsilon \end{aligned}$$

(A8)

and

$$\begin{aligned} \limsup _{N\rightarrow \infty } \sup _t |H_{x_N}(t) - H_{x}(t)|\le \epsilon . \end{aligned}$$

(A9)

We consider (A8) firstly. By Lemma 3, there exists $-\infty =t_0<t_1<\cdots <t_k=\infty$ such that for $0\le j\le k-1$, $H_{x_N}(t_{j+1}) - H_{x_N}(t_j)\le \frac{\epsilon }{2}$ for all n sufficiently large. For any t, there exists j such that $t_j\le t \le t_{j+1}$. For such j,

$$\begin{aligned} H^N_{x_N}(t_j) \le H^N_{x_N}(t) \le H^N_{x_N}(t_{j+1}) \;\; {\text {and}} \;\; H_{x_N}(t_j) \le H_{x_N}(t) \le H_{x_N}(t_{j+1}), \end{aligned}$$

which implies

$$\begin{aligned} H^N_{x_N}(t_j) -H_{x_N}(t_{j+1}) \le H^N_{x_N}(t) - H_{x_N}(t) \le H^N_{x_N}(t_{j+1}) - H_{x_N}(t_j). \end{aligned}$$

Then we have

$$\begin{aligned} H^N_{x_N}(t_j) - H_{x_N}(t_j) + H_{x_N}(t_j) -H_{x_N}(t_{j+1}) \le H^N_{x_N}(t) - H_{x_N}(t) \end{aligned}$$

and

$$\begin{aligned} H^N_{x_N}(t_{j+1}) - H_{x_N}(t_{j+1}) + H_{x_N}(t_{j+1}) - H_{x_N}(t_j) \ge H^N_{x_N}(t) - H_{x_N}(t). \end{aligned}$$

Note that by Lemma 3 and by uniform law of large numbers [27, Theorem 7.48], $H_{x_N}(t_{j+1}) - H_{x_N}(t_j)\le \frac{\epsilon }{2}$ and $|H^N_{x_N}(t_{j+1}) - H_{x_N}(t_j)|\le \frac{\epsilon }{4}$ for all N sufficiently large and $j=0, \ldots , k$, then we have (A8). Now we consider (A9). Similar as the procedure above, For any t, there exists j such that $t_j\le t \le t_{j+1}$. For such j,

$$\begin{aligned} H_x(t_j) \le H_{x}(t) \le H_x(t_{j+1}) \;\; {\text {and}} \;\; H_{x_N}(t_j) \le H_{x_N}(t) \le H(x_N, t_{j+1}). \end{aligned}$$

Then by continuous distribution of ${\mathbb {P}}$, Lipschitz continuity of $f(x, \xi )$ w.r.t. x and Lemma 3, for any $t\in {\mathbb {R}}$,

$$\begin{aligned} \begin{array}{lll} |H_{x_N}(t) - H_{x}(t)| &{} \le &{} |H_{x}(t) - H_{x_N}(t_j)| + |H_{x_N}(t_j) - H_x(t_j)| + |H_x(t_j) - H_{x}(t)|\\ &{} \le &{} |H_{x_N}(t_{j+1}) - H_{x_N}(t_j)| \\ &{}&{}+ |H_{x_N}(t_j) - H_x(t_j)| + |H_x(t_j) - H_x(t_{j+1})|\le \epsilon . \end{array} \end{aligned}$$

Combining (A8) and (A9), we have (A7).

Moreover, (A7) implies that $(H^N_{x_N})^{-1}$ pointwise converges to $H^{-1}_{x}$ on the set [0, 1]. Then, if the sequence $\{|(H^N_{x_N})^{-1}(s) - H^{-1}_{x}(s)|^p\}$ is uniformly integrable, $(H^N_{x_N})^{-1}$ converges w.p.1 to $H_{x}^{-1}$ in the norm topology of ${{\mathcal {L}}}_p$ as $N\rightarrow \infty$, that is w.p.1

$$\begin{aligned} \lim _{N\rightarrow \infty }\int _{0}^1|(H^N_{x_N})^{-1}(s) - H^{-1}_{x}(s)|^pds =\int _{0}^1 \lim _{N\rightarrow \infty }|(H^N_{x_N})^{-1}(s) - H^{-1}_{x}(s)|^pds =0, \end{aligned}$$

where the first equality comes from the Lebesgue’s dominated convergence theorem.

Let us show that the uniform integrability indeed holds. By triangle inequality,

$$\begin{aligned} |(H^N_{x_N})^{-1}(s) - H^{-1}_{x}(s)|^p\le |(H^N_{x_N})^{-1}(s)|^p + | H^{-1}_{x}(s)|^p. \end{aligned}$$

Then we only need to show the uniform integrability of $|(H^N_{x_N})^{-1}(s)|^p$. Note that

$$\begin{aligned} \int _{0}^{1} |(H^N_{x_N})^{-1}(s)|^pds = \int _{\Xi } |f(x_N, \xi )|^pdH^N_{x_N} =\frac{1}{N}\sum _{i=1}^N|f(x_N, \xi ^i)|^p. \end{aligned}$$

Since the Lipschitz continuity of $f(x, \xi )$ with Lipschitz modules $\kappa (\xi )$,

$$\begin{aligned}&|\frac{1}{N}\sum \limits _{i=1}^N|f(x_N, \xi ^i)|^p - {\mathbb {E}}_{\mathbb {P}}[|f(x, \xi )|^p]| \\&\qquad \qquad \le |\frac{1}{N}\sum \limits _{i=1}^N|f(x_N, \xi ^i)|^p - \frac{1}{N}\sum \limits _{i=1}^N|f(x, \xi ^i)|^p| \\&\qquad \qquad \quad + |\frac{1}{N}\sum \limits _{i=1}^N|f(x, \xi ^i)|^p - {\mathbb {E}}_{\mathbb {P}}[|f(x, \xi )|^p]|\\&\quad \qquad \le |\frac{1}{N}\sum \limits _{i=1}^N\kappa (\xi )(x-x_N) |^p \\&\qquad \qquad \quad + |\frac{1}{N}\sum \limits _{i=1}^N|f(x, \xi ^i)|^p - {\mathbb {E}}_{\mathbb {P}}[|f(x, \xi )|^p]|. \end{aligned}$$

Moreover, by the law of large numbers and $x_N\rightarrow x$, $\frac{1}{N}\sum _{i=1}^N\kappa (\xi )\rightarrow {\mathbb {E}}_{\mathbb {P}}[\kappa (\xi )]$, $|\frac{1}{N}\sum _{i=1}^N\kappa (\xi )(x-x_N) |^p\rightarrow 0$ and $|\frac{1}{N}\sum _{i=1}^N|f(x, \xi ^i)|^p - {\mathbb {E}}_{\mathbb {P}}[|f(x, \xi )|^p]|\rightarrow 0$ as $N\rightarrow \infty$ w.p.1. It follows that $|(H^N_{x_N})^{-1}(s)|^p$ converges w.p.1 to a finite limit, which implies that w.p.1 $|(H^N_{x_N})^{-1}(s)|^p$ is uniformly integrable. $\square$

Proof of Proposition 4

For any continuous and bounded function $g:\Xi \rightarrow {\mathbb {R}}$, we have that

$$\begin{aligned} \int _\Xi g(s){\bar{\zeta }}^{{\bar{x}}}(s)d{\mathbb {P}}(s)= & {} \int _{{[0,1)}}\int _\Xi g(s){\bar{\zeta }}_\alpha ^{{\bar{x}}}(s)d{\mathbb {P}}(s) d{\bar{\mu }}(\alpha )\\= & {} \int _{{[0,1)}}\frac{1}{1-\alpha }\int _{\phi ^{{\bar{x}}}(\xi )>\kappa _\alpha } g(s)d{\mathbb {P}}(s)d{\bar{\mu }}(\alpha ), \end{aligned}$$

where ${\bar{\mu }}$ is corresponding to ${\bar{\sigma }}$. Moreover,

$$\begin{aligned} \int _\Xi g(s) dP^{x_N}_{N}(s)= & {} \int _{{[0,1)}} \frac{1}{N}\sum _{j=1}^Ng(\xi ^j)(\zeta _j^{x_N})_\alpha d\mu _N(\alpha )\\= & {} \int _{{[0,1)}}\frac{1}{(1-\alpha ) N}\sum _{\phi ^{x_N}(\xi ^j)>\kappa ^\alpha _{N,x_N}} g(\xi ^j) d\mu _N(\alpha ). \end{aligned}$$

Then

$$\begin{aligned} \begin{array}{lll} |\int _\Xi g(s) dP^{x_N}_{N}(s) - \int _\Xi g(s){\bar{\zeta }}^{{\bar{x}}}(s)d{\mathbb {P}}(s)| \\ \quad \le \displaystyle {\left| \int _{{[0,1)}}\frac{1}{(1-\alpha ) N}\sum _{\phi ^{x_N}(\xi ^j)>\kappa ^\alpha _{N,x_N}} g(\xi ^j) d\mu _N(\alpha ) - \int _{{[0,1)}}\frac{1}{1-\alpha }\int _{\phi ^{{\bar{x}}}(\xi )>\kappa _\alpha } g(s)d{\mathbb {P}}(s)d\mu _N(\alpha )\right| } \\ \quad +\displaystyle {\left| \int _{{[0,1)}}\frac{1}{1-\alpha }\int _{\phi ^{{\bar{x}}}(\xi )>\kappa _\alpha } g(s)d{\mathbb {P}}(s) d\mu _N(\alpha ) - \int _{{[0,1)}}\frac{1}{1-\alpha }\int _{\phi ^{{\bar{x}}}(\xi )>\kappa _\alpha } g(s)d{\mathbb {P}}(s)d{\bar{\mu }}(\alpha )\right| }. \end{array}\nonumber \\ \end{aligned}$$

(A10)

We first prove

$$\begin{aligned} \displaystyle {\left| \int _{{[0,1)}}\frac{1}{1-\alpha }\int _{\phi ^{{\bar{x}}}(\xi )>\kappa _\alpha } g(s)d{\mathbb {P}}(s) d\mu _N(\alpha ) - \int _{{[0,1)}}\frac{1}{1-\alpha }\int _{\phi ^{{\bar{x}}}(\xi )>\kappa _\alpha } g(s)d{\mathbb {P}}(s)d{\bar{\mu }}(\alpha )\right| } \rightarrow 0 \nonumber \\ \end{aligned}$$

(11)

as $N\rightarrow \infty$. From condition (iii), $g(\xi )$ is continuous and bounded and $\phi ^{{\bar{x}}}(\xi )$ is continuous w.r.t. $\xi$. Then for any $\alpha '\rightarrow \alpha$, $\alpha ', \alpha \in [0, 1)$, we have

$$\begin{aligned} \left| \int _{\phi ^{{\bar{x}}}(\xi )>\kappa _{\alpha '}} g(s)d{\mathbb {P}}(s) - \int _{\phi ^{{\bar{x}}}(\xi )>\kappa _\alpha } g(s)d{\mathbb {P}}(s) \right| \le {\mathbb {P}}((A_{\alpha '} - A_\alpha )\cup (A_{\alpha } - A_{\alpha '}))\max _sg(s), \end{aligned}$$

where $A_\alpha = \{\xi : \phi ^{{\bar{x}}}(\xi )>\kappa _\alpha \}$ and $A_{\alpha '} = \{\xi : \phi ^{{\bar{x}}}(\xi )>\kappa _{\alpha '}\}$. Note that $a'\rightarrow a$ and the CDF of $\phi ^{{\bar{x}}}$ is strictly monotone, $A_{\alpha '}\rightarrow A_\alpha$ and ${\mathbb {P}}((A_{\alpha '} - A_\alpha )\cup (A_{\alpha } - A_{\alpha '}))\rightarrow 0$. Then we have that $\frac{1}{1-\alpha }\int _{\phi ^{{\bar{x}}}(\xi )>\kappa _\alpha } g(s)d{\mathbb {P}}(s)$ is continuous and bounded w.r.t. $\alpha$, and (11) is from the fact that $\mu _N$ weak* converges to $\mu$. Indeed, by Lemma 2, $\sigma _N$ weak* converges to ${\bar{\sigma }}$, then for any continuous and bounded function g(t), $\int _{[0,1)}g(t)\sigma _N(t)dt\rightarrow \int _{[0,1)}g(t){\bar{\sigma }}(t)dt$ as $N\rightarrow \infty$. Note that $\mu (\alpha ) = (1-\alpha )\sigma (\alpha ) + \int _{0}^\alpha \sigma (t)dt$. Then

$$\begin{aligned}&|\int _{[0,1)}g(\alpha )\mu _N(\alpha )d\alpha - \int _{[0,1)}g(\alpha ){\bar{\mu }}(\alpha )d\alpha |\\&\quad = (1-\alpha )|\int _{[0,1)}g(\alpha )\sigma _N(\alpha )d\alpha - \int _{[0,1)}g(\alpha ){\bar{\sigma }}(\alpha )d\alpha |\\&\quad + \int _{[0,1)} \int _{0}^\alpha g(\alpha ) (\sigma _N(t) - {\bar{\sigma }}(t))dt d\alpha \rightarrow 0 \end{aligned}$$

as $N\rightarrow \infty$, which implies that $\mu _N$ weak* converges to ${\bar{\mu }}$.

Then we prove

$$\begin{aligned} \displaystyle {\left| \int _{{[0,1)}}\frac{1}{(1-\alpha ) N}\sum _{\phi ^{x_N}(\xi ^j)>\kappa ^\alpha _{N,x_N}} g(\xi ^j) d\mu _N(\alpha ) - \int _{{[0,1)}}\frac{1}{1-\alpha }\int _{\phi ^{{\bar{x}}}(\xi )>\kappa _\alpha } g(s)d{\mathbb {P}}(s) d\mu _N(\alpha )\right| } \rightarrow 0. \end{aligned}$$

Note that $\phi ^{{\bar{x}}}(\xi )$ is Lipschitz continuous w.r.t. x, the given g is continuous and bounded function w.r.t. $\xi$ and $\{\xi ^j\}_{j=1}^N$ is i.i.d. samples from ${\mathbb {P}}$, both $\frac{1}{(1-\alpha ) N}\sum _{\phi ^{x_N}(\xi ^j)>\kappa ^\alpha _{N,x_N}} g(\xi ^j)$ and $\frac{1}{1-\alpha }\int _{\phi ^{{\bar{x}}}(\xi )>\kappa _\alpha } g(s)d{\mathbb {P}}(s)$ are bounded by $\max _{s\in [0,1]} g(s)$ and by Proposition 6

$$\begin{aligned} \lim _{N\rightarrow \infty }\left| \frac{1}{(1-\alpha ) N}\sum _{\phi ^{x_N}(\xi ^j)>\kappa ^\alpha _{N,x_N}} g(\xi ^j) - \frac{1}{1-\alpha }\int _{\phi ^{{\bar{x}}}(\xi )>\kappa _\alpha } g(s)d{\mathbb {P}}(s) \right| = 0. \end{aligned}$$

We then have

$$\begin{aligned}&{\displaystyle \lim _{N\rightarrow \infty }\left| \int _{{[0,1)}}\frac{1}{(1-\alpha ) N}\sum _{\phi ^{x_N}(\xi ^j)>\kappa ^\alpha _{N,x_N}} g(\xi ^j) d\mu _N(\alpha ) \right. }\\&\quad - {\displaystyle \left. \int _{{[0,1)}}\frac{1}{1-\alpha }\int _{\phi ^{{\bar{x}}}(\xi )>\kappa _\alpha } g(s)d{\mathbb {P}}(s) d\mu _N(\alpha )\right| } \\&\quad \le {\displaystyle \lim _{N\rightarrow \infty }\int _{{[0,1)}}\left| \frac{1}{\alpha N}\sum _{\phi ^{x_N}(\xi ^j)>\kappa ^\alpha _{N,x_N}} g(\xi ^j) - \int _{{[0,1)}}\frac{1}{\alpha }\int _{\phi ^{{\bar{x}}}(\xi )>\kappa _\alpha } g(s)d{\mathbb {P}}(s)\right| d\mu _N(\alpha )}\\&\quad \le {\displaystyle \lim _{N\rightarrow \infty }\int _{{[0,1)}}\left| \frac{1}{\alpha N}\sum _{\phi ^{x_N}(\xi ^j)>\kappa ^\alpha _{N,x_N}} g(\xi ^j) - \int _{{[0,1)}}\frac{1}{\alpha }\int _{\phi ^{{\bar{x}}}(\xi )>\kappa _\alpha } g(s)d{\mathbb {P}}(s)\right| d{\hat{\mu }}(\alpha )}\\&\quad = 0, \end{aligned}$$

where the second inequality is from condition (iii) and the third equality is from Lebesgue’s dominated convergence theorem.

Combining the above analysis, we have (A10), that is $P^{x_N}_{N}$ converges weakly to $P^{{\bar{x}}}$. $\square$

Proof of Theorem 2

By conditions (c)–(e),

$$\begin{aligned} P^{{\bar{x}}}\in \arg \max _{Q\in {{\mathfrak {M}}}} {\mathbb {E}}_Q[\phi ({\bar{x}},\xi )]. \end{aligned}$$

Then we only need to prove that ${\bar{x}}$ is a solution of (22), which is equivalent to

$$\begin{aligned} 0\in {\mathbb {E}}_{P^{{\bar{x}}}}[\varPhi ({\bar{x}},\xi )]+ {{\mathcal {N}}}_X({\bar{x}}). \end{aligned}$$

(A12)

Since ${\hat{x}}_N\rightarrow {\bar{x}}$,

$$\begin{aligned} \limsup _{N\rightarrow \infty } {{\mathcal {N}}}_{X}({\hat{x}}_N)\subset {{\mathcal {N}}}_{X}({\bar{x}}). \end{aligned}$$

(A13)

Moreover,

$$\begin{aligned} \begin{array}{lll} \Vert {\mathbb {E}}_{P_N^{{\hat{x}}_N}}[\varPhi ({\hat{x}}_N,\xi )] - {\mathbb {E}}_{P^{{\bar{x}}}}[\varPhi ({\bar{x}},\xi )] \Vert &{}\le &{} \Vert {\mathbb {E}}_{P_N^{{\hat{x}}_N}}[\varPhi ({\hat{x}}_N,\xi )] - {\mathbb {E}}_{P^{{\bar{x}}}}[\varPhi ({\hat{x}}_N,\xi )] \Vert \\ &{} + &{} \Vert {\mathbb {E}}_{P^{{\bar{x}}}}[\varPhi ({\hat{x}}_N,\xi )] - {\mathbb {E}}_{P^{{\bar{x}}}}[\varPhi ({\bar{x}}, \xi )] \Vert . \end{array} \end{aligned}$$

Note that since $P_N^{{\hat{x}}_N} \rightarrow P^{{\bar{x}}}$ weakly and by Assumption 3 (b), $P_N^{{\hat{x}}_N} \rightarrow P^{{\bar{x}}}$ under Kantorovich metric [23]. Then by condition (b), we have for any N, $\varPhi ({\hat{x}}_N, \cdot )$ is Lipschitz continuous and

$$\begin{aligned} \lim _{N\rightarrow \infty }\sup _{z\in {\bar{Z}}}\Vert {\mathbb {E}}_{P_N^{{\hat{x}}_N}}[\varPhi (z,\xi )] - {\mathbb {E}}_{P^{{\bar{x}}}}[\varPhi (z,\xi )] \Vert =0, \end{aligned}$$

(A14)

where ${\bar{Z}}:=\{{\hat{x}}_N, N=1, 2, \cdots \}$. Moreover,

$$\begin{aligned} \displaystyle {\lim _{N\rightarrow \infty }}\Vert {\mathbb {E}}_{P^{{\bar{x}}}}[\varPhi ({\bar{x}},\xi )] - {\mathbb {E}}_{P^{{\bar{x}}}}[\varPhi ({\hat{x}}_N,\xi )] \Vert\le & {} \displaystyle {\lim _{N\rightarrow \infty }}{\mathbb {E}}_{P^{{\bar{x}}}}[\kappa (\xi )]\Vert {\bar{x}}-{\hat{x}}_N\Vert \nonumber \\\le & {} \displaystyle {\lim _{N\rightarrow \infty }}\sup _{P\in {\hat{{{\mathfrak {M}}}}}}{\mathbb {E}}_P[\kappa (\xi )]\Vert {\bar{x}}-{\hat{x}}_N\Vert \nonumber \\= & {} 0. \end{aligned}$$

(A15)

Combining (A14)–(A15), we have

$$\begin{aligned} \lim _{N\rightarrow \infty }\Vert {\mathbb {E}}_{P_N^{{\hat{x}}_N}}[\varPhi ({\hat{x}}_N,\xi )] - {\mathbb {E}}_{P^{{\bar{x}}}}[\varPhi ({\bar{x}},\xi )] \Vert =0. \end{aligned}$$

(A16)

Hence from (A13) and (A16), we obtain (A12). $\square$