Abstract
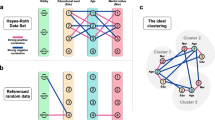
The demand on cluster analysis for categorical data continues to grow over the last decade. A well-known problem in categorical clustering is to determine the best K number of clusters. Although several categorical clustering algorithms have been developed, surprisingly, none has satisfactorily addressed the problem of best K for categorical clustering. Since categorical data does not have an inherent distance function as the similarity measure, traditional cluster validation techniques based on geometric shapes and density distributions are not appropriate for categorical data. In this paper, we study the entropy property between the clustering results of categorical data with different K number of clusters, and propose the BKPlot method to address the three important cluster validation problems: (1) How can we determine whether there is significant clustering structure in a categorical dataset? (2) If there is significant clustering structure, what is the set of candidate “best Ks”? (3) If the dataset is large, how can we efficiently and reliably determine the best Ks?
Similar content being viewed by others
References
Aggarwal CC, Magdalena C, Yu PS (2002) Finding localized associations in market basket data. IEEE Trans Knowl Data Eng 14(1): 51–62
Agresti A (1990) Categorical Data Analysis. Wiley, NY
Andritsos P, Tsaparas P, Miller RJ, Sevcik KC (2004) Limbo:scalable clustering of categorical data. In: Proceedings of international conference on extending database technology (EDBT)
Ankerst M, Breunig MM, Kriegel HP, Sander J (1999) OPTICS: Ordering points to identify the clustering structure. In: Proceedings of ACM SIGMOD conference, pp 49–60
Barbara D, Jajodia S (eds) (2002) Applications of data mining in computer security. Kluwer, Dordrecht
Barbara D, Li Y, Couto J (2002) Coolcat: an entropy-based algorithm for categorical clustering. In: Proceedings of ACM conference on information and knowledge management (CIKM)
Baulieu F (1997) Two variant axiom systems for presence/absence based dissimilarity coefficients. J Classif 14
Baxevanis A, Ouellette F (eds) (2001) Bioinformatics: a practical guide to the analysis of genes and proteins, 2nd edn. Wiley, NY
Bock H (1989) Probabilistic aspects in cluster analysis. In: Conceptual and numerical analysis of data. Springer, Berlin
Brand M (1998) An entropic estimator for structure discovery. In: Proceedings Of neural information processing systems (NIPS). pp 723–729
Celeux G, Govaert G (1991) Clustering criteria for discrete data and latent class models. J Classif
Chakrabarti D, Papadimitriou S, Modha DS, Faloutsos C (2004) Fully automatic cross-associations. In: Proceedings of ACM SIGKDD conference
Chen K, Liu L (2004) VISTA: Validating and refining clusters via visualization. Inf Vis 3(4): 257–270
Chen K, Liu L (2005) The “best k” for entropy-based categorical clustering. In: Proceedings of international conference on scientific and statistical database management (SSDBM). pp 253–262
Chen K, Liu L (2006) Detecting the change of clustering structure in categorical data streams. In: SIAM data mining conference
Cheng CH, Fu AW-C, Zhang Y (1999) Entropy-based subspace clustering for mining numerical data. In: Proceedings of ACM SIGKDD conference
Cover T, Thomas J (1991) Elements of information theory. Wiley, NY
Dhillon IS, Mellela S, Modha DS (2003) Information-theoretic co-clustering. In: Proceedings of ACM SIGKDD conference
Ester M, Kriegel H-P, Sander J, Xu X (1996) A density-based algorithm for discovering clusters in large spatial databases with noise. In: Second international conference on knowledge discovery and data mining, pp 226–231
Ganti V, Gehrke J, Ramakrishnan R (1999) CACTUS-clustering categorical data using summaries. In: Proceedings of ACM SIGKDD Conference
Gibson D, Kleinberg J, Raghavan P (2000) Clustering categorical data: An approach based on dynamical systems. In: Proceedings of very large databases conference (VLDB). pp 222–236
Gondek D, Hofmann T (2007) ‘Non-redundant data clustering’. Knowl Inf Syst 12(1): 1–24
Guha S, Rastogi R, Shim K (2000) ROCK: A robust clustering algorithm for categorical attributes. Inf Syst 25(5): 345–366
Halkidi M, Batistakis Y, Vazirgiannis M (2002) Cluster validity methods: Part I and II. SIGMOD Rec 31(2): 40–45
Hastie T, Tibshirani R, Friedmann J (2001) The elements of statistical learning. Springer, Berlin
Huang Z (1997) A fast clustering algorithm to cluster very large categorical data sets in data mining. In: Workshop on research issues on data mining and knowledge discovery
Jain AK, Dubes RC (1988) Algorithms for clustering data. Prentice hall, New York
Jain AK, Dubes RC (1999) Data clustering: a review. ACM Comput Surv 31: 264–323
Lehmann EL, Casella G (1998) Theory of Point Estimation. Springer, Berlin
Li T, Ma S, Ogihara M (2004) Entropy-based criterion in categorical clustering. In: Proceedings of international conference on machine learning (ICML)
Meek C, Thiesson B, Heckerman D (2002) The learning-curve sampling method applied to model-based clustering. J Mach Learn Res 2: 397–418
Sharma S (1995) Applied multivariate techniques. Wiley, NY
Tishby N, Pereira FC, Bialek W (1999) The information bottleneck method. In: Proceedings of the 37-th annual allerton conference on communication, control and computing
Wang J, Karypis G (2006) ‘On efficiently summarizing categorical databases’. Knowl Inf Syst 9(1): 19–37
Wrigley N (1985) Categorical data analysis for geographers and environmental scientists. Longman, London
Yu JX, Qian W, Lu H, Zhou A (2006) Finding centric local outliers in categorical/numerical spaces. Knowl Inf Syst 9(3): 309–338
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Chen, K., Liu, L. “Best K”: critical clustering structures in categorical datasets. Knowl Inf Syst 20, 1–33 (2009). https://doi.org/10.1007/s10115-008-0159-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10115-008-0159-x