A new multiobjective clustering technique based on the concepts of stability and symmetry

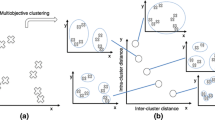
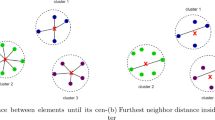
Abstract

Most clustering algorithms operate by optimizing (either implicitly or explicitly) a single measure of cluster solution quality. Such methods may perform well on some data sets but lack robustness with respect to variations in cluster shape, proximity, evenness and so forth. In this paper, we have proposed a multiobjective clustering technique which optimizes simultaneously two objectives, one reflecting the total cluster symmetry and the other reflecting the stability of the obtained partitions over different bootstrap samples of the data set. The proposed algorithm uses a recently developed simulated annealing-based multiobjective optimization technique, named AMOSA, as the underlying optimization strategy. Here, points are assigned to different clusters based on a newly defined point symmetry-based distance rather than the Euclidean distance. Results on several artificial and real-life data sets in comparison with another multiobjective clustering technique, MOCK, three single objective genetic algorithm-based automatic clustering techniques, VGAPS clustering, GCUK clustering and HNGA clustering, and several hybrid methods of determining the appropriate number of clusters from data sets show that the proposed technique is well suited to detect automatically the appropriate number of clusters as well as the appropriate partitioning from data sets having point symmetric clusters. The performance of AMOSA as the underlying optimization technique in the proposed clustering algorithm is also compared with PESA-II, another evolutionary multiobjective optimization technique.