A new approach for maximizing bichromatic reverse nearest neighbor search

Abstract

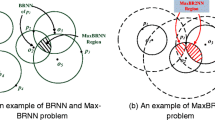
Maximizing bichromatic reverse nearest neighbor (MaxBRNN) is a variant of bichromatic reverse nearest neighbor (BRNN). The purpose of the MaxBRNN problem is to find an optimal region that maximizes the size of BRNNs. This problem has lots of real applications such as location planning and profile-based marketing. The best-known algorithm for the MaxBRNN problem is called MaxOverlap. In this paper, we study the MaxBRNN problem and propose a new approach called MaxSegment for a two-dimensional space when the $L_2$-norm is used. Then, we extend our algorithm to other variations of the MaxBRNN problem such as the MaxBRNN problem with other metric spaces, and a three-dimensional space. Finally, we conducted experiments on real and synthetic datasets to compare our proposed algorithm with existing algorithms. The experimental results verify the efficiency of our proposed approach.

Appendix: Computation of \((s_1, s_2)\)-circle, \((s_2, s_2)\)-plane and \(s_3\)-circle on plane in a three-dimensional space

In Sect. 5.3, given three NLSs, namely $s_1, s_2$, and $s_3$ as shown in Fig. 10, we describe the concepts of the $(s_1, s_2)$-circle, the $(s_2, s_2)$-plane, and the $s_3$-circle on a plane. In this section, we describe how we compute these three concepts.

How to Compute $(s_1, s_2)$-Circle: In the following, we want to describe a method to compute the $(s_1, s_2)$-circle given two NLS $s_1$ and $s_2$.

Assume NLS $s_1$ centered at $o_1 (x_1, y_1, z_1)$ with radius $r_1$ and NLS $s_2$ centered at $o_2 (x_2, y_2, z_2)$ with radius $r_2$. Then, we would have the following equations.

$$\begin{aligned} (x-x_1)^2+(y-y_1)^2+(z-z_1)^2=r_1^2 \end{aligned}$$

(1)

$$\begin{aligned} (x-x_2)^2+(y-y_2)^2+(z-z_2)^2=r_2^2 \end{aligned}$$

(2)

From Eqs. (1) and (2), we have: $-2x(x_1-x_2)+(x_1^2-x_2^2)-2y(y_1-y_2)+(y_1^2-y_2^2)-2z(z_1-z_2)+(z_1^2-z_2^2)=r_1^2-r_2^2$ Next, we have

$$\begin{aligned} x(x_1-x_2)+y(y_1-y_2)+z(z_1-z_2)=\frac{r_1^2-r_2^2+x_2^2+y_2^2+z_2^2-x_1^2-y_1^2-z_1^2}{-2} \end{aligned}$$

(3)

We assume that the $(s_1, s_2)$-circle $c_{12}$ is centered at $o_{12} (x_{12}, y_{12}, z_{12})$ with radius $r_{12}$. In the following, we need to compute the coordinates of the three-dimensional point $o_{12}$ and the radius $r_{12}$. Since the point $o_{12}$ is along the line segment between $o_1$ and $o_2$, we can assume that $\overrightarrow{o_1o_{12}}=\lambda \overrightarrow{o_1o_{2}}$, $(0<\lambda <1)$. Then, we have

$$\begin{aligned} (x_1-x_{12},y_1-y_{12},z_1-z_{12})=\lambda (x_1-x_2,y_1-y_2,z_1-z_2) \end{aligned}$$

(4)

That is,

$$\begin{aligned} x_{12}=x_1+\lambda (x_2-x_1), y_{12}=y_1+\lambda (y_2-y_1), z_{12}=z_1+\lambda (z_2-z_1) \end{aligned}$$

(5)

Since the point $o_{12} (x_{12}, y_{12}, z_{12})$ is on the plane $\alpha$, we can put $x_{12}$, $y_{12}$ and $z_{12}$ in Eq. (5) into Eq. (3) (i.e., replacing $x$, $y$, $z$, respectively). Then, we have

$$\begin{aligned}&(x_1+\lambda (x_2-x_1))(x_1-x_2)+(y_1+\lambda (y_2-y_1))(y_1-y_2)\\&\quad +(z_1+\lambda (z_2-z_1))(z_1-z_2)\\&\quad = \frac{r_1^2-r_2^2+x_2^2+y_2^2+z_2^2-x_1^2-y_1^2-z_1^2}{-2} \end{aligned}$$

Next, we have $\lambda =\frac{r_1^2-r_2^2}{2(x_2-x_1)^2}+\frac{1}{2}$. Then, we put $\lambda$ into Eq. (5) and compute the coordinates of the three-dimensional point $o_{12}$. That is,

$$\begin{aligned} \left\{ \begin{array}{l} x_{12}=x_1+\left(\frac{r_1^2-r_2^2}{2(x_2-x_1)^2}+\frac{1}{2}\right)(x_2-x_1)\\ y_{12}=y_1+\left(\frac{r_1^2-r_2^2}{2(x_2-x_1)^2}+\frac{1}{2}\right)(y_2-y_1)\\ z_{12}=z_1+\left(\frac{r_1^2-r_2^2}{2(x_2-x_1)^2}+\frac{1}{2}\right)(z_2-z_1) \end{array}\right. \end{aligned}$$

(6)

where $o_1 (x_1, y_1, z_1)$, $o_2 (x_2, y_2, z_2)$, $r_1$, and $r_2$ are known.

The radius $r_{12}$ can be computed as follows. As shown in Fig. 10a, we can easily image the following sectional drawing in Fig. 20 for NLS $s_1$, NLS $s_2$, and circle $c_{12}$. So, we have $r_{12}=\sqrt{r_1^2-| o_1o_{12}|^2}=\sqrt{r_1^2-\lambda ^2|o_1o_2|^2}$, where $o_1$, $o_2$, $r_1$ and $\lambda$ are known. Thus, we derive the $(s_1, s_2)$-circle.

Fig. 20

A sectional drawing for $s_1$, $s_2$ and $c_{12}$

It is easy to verify that the above computation of the $(s_1, s_2)$-circle takes $O(1)$ time.

How to Compute $(s_1, s_2)$ -Plane and $s_3$-Circle: In the following, we describe how to compute the $(s_1, s_2)$-plane, says $\alpha$, and the $s_3$-circle on plane $\alpha$, says $c_3$.

Assume that NLS $s_3$ is centered at $o_3 (x_3, y_3, z_3)$ with radius $r_3$. Assume the center of circle $c_3$ in the three-dimensional space is $o_{c3} (x_{c3},$ $y_{c3}, z_{c3})$ and its radius is $r_{c3}$. From Fig. 10, it is easy to know that both points $o_{12}$ and $o_{c3}$ are on the plane $\alpha$. We can build a coordinate system, $X_\alpha Y_\alpha$, on the two-dimensional plane $\alpha$ whose origin is $o_{12}$. The relationship between the three-dimensional space and the two-dimensional plane $\alpha$ can be shown in Fig. 21. From Fig. 21, we can know the coordinates of point $o_{c3}$ in the two-dimensional space $(X_{\alpha }, Y_{\alpha })$ correspond to $u$ and $v$, respectively. Before computing $u$ and $v$, we need to find the vectors $\overrightarrow{X_\alpha }$ and $\overrightarrow{Y_\alpha }$ that correspond to the axes of the coordinate system on the two-dimensional plane $\alpha$. From Fig. 10a, we can know the normal vector $\overrightarrow{N}=\overrightarrow{o_2}-\overrightarrow{o_1}$ to the plane $\alpha$. That is, we have $\overrightarrow{N} = (x_2-x_1, y_2-y_1, z_2- z_1)$. This normal vector can denote the $(s_1, s_2)$-plane.

Fig. 21

The computation for the circle $c_3$

Next, we construct two vectors as follows.

$$\begin{aligned} \left\{ \begin{array}{l} X_\alpha =(y_2-y_1,x_1-x_2,0) \\ Y_\alpha =\left(\frac{-(x_2-x_1)(z_2-z_1)}{(x_2-x_1)^2+(y_2-y_1)^2},\frac{-(y_2-y_1)(z_2-z_1)}{(x_2-x_1)^2+(y_2-y_1)^2},1\right) \end{array}\right. \end{aligned}$$

(7)

It is easy to verify the vectors $\overrightarrow{X_\alpha }$, $\overrightarrow{Y_\alpha }$, and $\overrightarrow{N}$ are perpendicular to each of the other two vectors. Then, we can take $\overrightarrow{X_\alpha }$ and $\overrightarrow{Y_\alpha }$ as the axes of the coordinate system on the two-dimensional plane $\alpha$. It is also easy to know that $\overrightarrow{o_{c3}o_3}=\varphi \overrightarrow{N}$, where $\varphi$ is a real number and $\overrightarrow{N}$ is the normal vector to the plane $\alpha$. Then, we have the following Eq. (8) in which $x_N$, $y_N$, and $z_N$ denote the vector components of vector $\overrightarrow{N}$, respectively.

$$\begin{aligned} x_3-x_{c3}=\varphi x_N, y_3-y_{c3}=\varphi y_N,z_3-z_{c3}=\varphi z_N \end{aligned}$$

(8)

Since $\overrightarrow{o_{12}o_{c3}}\perp \overrightarrow{N}$,we have $(x_{c3}-x_{12})x_N + (y_{c3}-y_{12})y_N + (z_{c3}-z_{12})z_N = 0$. Next, we can replace $x_{c3}$, $y_{c3}$ and $z_{c3}$ using Eq. (8).

Then, we have $\varphi =\frac{x_N (x_3-x_{12})+ y_N(y_3-y_{12}) + z_N(z_3-z_{12})}{x_N^2 + y_N^2 + z_N^2}$. Next, we put $\varphi$ into Eq. (8) and have $o_{c3} (x_{c3}, y_{c3}, z_{c3})$. That is,

$$\begin{aligned} \left\{ \begin{array}{l} x_{c3}=x_3-\varphi x_N \\ y_{c3}=y_3-\varphi y_N \\ z_{c3}=z_3-\varphi z_N \end{array}\right. \end{aligned}$$

(9)

where $x_3$, $y_3$, $z_3$, $x_N$, $y_N$, $z_N$, and $\varphi$ are known. From Fig. 21, we have $u$, $v$ and the radius of $c_3$ as follows.

$$\begin{aligned} \left\{ \begin{array}{l} u=|o_{12}o_{c3}| \cdot \cos {\theta }=\frac{\overrightarrow{o_{12}o_{c3}}\cdot \overrightarrow{X_\alpha }}{|X_\alpha |}\\ v=|o_{12}o_{c3}| \cdot \sin {\theta }=\frac{\overrightarrow{o_{12}o_{c3}}\cdot \overrightarrow{Y_\alpha }}{|Y_\alpha |}\\ r_{c3}=\sqrt{r_3^2-|o_3o_{c3}|^2} \end{array}\right. \end{aligned}$$

(10)

where $r_3$, $o_3$, $o_{c3}$, $\overrightarrow{X_\alpha }$ and $\overrightarrow{Y_\alpha }$ are known. Thus, we derive the $s_3$-circle.

It is easy to verify that the computation of the $(s_1, s_2)$-plane and the $s_3$-circle takes $O(1)$ time.