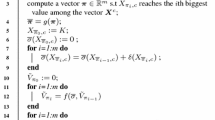Skip to main content

Advertisement

Springer Nature Link
Log in

A novel correlation Gaussian process regression-based extreme learning machine

  • Regular Paper
  • Published:
Knowledge and Information Systems Aims and scope Submit manuscript

This article has been updated

Abstract

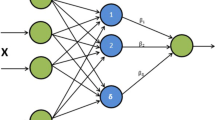
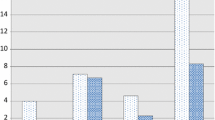
An obvious defect of extreme learning machine (ELM) is that its prediction performance is sensitive to the random initialization of input-layer weights and hidden-layer biases. To make ELM insensitive to random initialization, GPRELM adopts the simple an effective strategy of integrating Gaussian process regression into ELM. However, there is a serious overfitting problem in kernel-based GPRELM (kGPRELM). In this paper, we investigate the theoretical reasons for the overfitting of kGPRELM and further propose a correlation-based GPRELM (cGPRELM), which uses a correlation coefficient to measure the similarity between two different hidden-layer output vectors. cGPRELM reduces the likelihood that the covariance matrix becomes an identity matrix when the number of hidden-layer nodes is increased, effectively controlling overfitting. Furthermore, cGPRELM works well for improper initialization intervals where ELM and kGPRELM fail to provide good predictions. The experimental results on real classification and regression data sets demonstrate the feasibility and superiority of cGPRELM, as it not only achieves better generalization performance but also has a lower computational complexity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Change history

  • 18 January 2023

    Author biography details has been updated.

Abbreviations

ELM:

Extreme learning machine

SLFN:

Single hidden-layer feed-forward network

BP:

Back-propagation

BLRELM:

Bayesian linear regression-based ELM

GPR:

Gaussian process regression

GPRELM:

GPR-based ELM

1HNBKM:

One hidden-layer nonparametric Bayesian kernel machine

RBF:

Radial basis function

kGPRELM:

Kernel-based GPRELM

cGPRELM:

Correlation-based GPRELM

SVM:

Support vector machine

LSSVM:

Least square SVM

UCI:

University of California, Irvine

KEEL:

Knowledge extraction based on evolutionary learning

RMSE:

Root-mean-square error

\(\mathrm{{D}}\) :

Training data set

N :

Number of instances in \(\mathrm{{D}}\)

\({\mathrm{{x}}_i}\) :

Input of the i-th training instance

\({\mathrm{{y}}_i}\) :

Output of the i-th training instance

D :

Number of instance’s condition attributes

M :

Number of instance’s decision attributes

\(\mathrm{{W}}\) :

Input-layer matrix of ELM

\({{w_{dl}}}\) :

Weight on the link between the d-th input-layer node and the l-th hidden-layer node

\(\mathrm{{b}}\) :

Hidden-layer bias vector of ELM

\({b_l}\) :

Bias of the l-th hidden-layer node

\(\mathrm{{H}}\) :

Hidden-layer output matrix of ELM

\(\mathrm{{h}}\left( {{\mathrm{{x}}_i}} \right) \) :

Hidden-layer output of i-th training instance

\(\beta \) :

Output-layer matrix of ELM

\(g\left( \cdot \right) \) :

Activation function of hidden-layer node

\(k\left( { \cdot , \cdot } \right) \) :

Kernel function

\(\lambda \) :

Kernel radius of kernel function \(k\left( { \cdot , \cdot } \right) \)

\(\mu \) :

Mean of Gaussian distribution

\(\sigma _N^2\) :

Variance of Gaussian distribution

\(\varepsilon \) :

Gaussian noise

\(\mathrm{{I}}\) :

Identity matrix

\(\mathrm{{C}}\) :

Correlation matrix

\(c\left( { \cdot , \cdot } \right) \) :

Correlation function

\(\mathrm{{Cov}}\left( {\mathrm{{u}},\mathrm{{v}}} \right) \) :

Covariance between vectors \(\mathrm{{u}}\) and \(\mathrm{{v}}\)

\(\mathrm{{Var}}\left( {\mathrm{{u}}} \right) \) :

Variance of vector \(\mathrm{{u}}\)

References

  1. Alcalá-Fdez J, Fernandez A, Luengo J, Derrac J, García S, Sánchez L, Herrera F (2011) KEEL data-mining software tool: data set repository, integration of algorithms and experimental analysis framework. J Mult-Valued Logic Soft Comput 17(2–3):255–287

    Google Scholar 

  2. Cao JW, Lin ZP, Huang GB (2012) Self-adaptive evolutionary extreme learning machine. Neural Process Lett 36(3):285–305

    Article  Google Scholar 

  3. Chatzis SP, Korkinof D, Demiris Y (2011) The one-hidden layer non-parametric Bayesian kernel machine, In: Proceedings of IEEE international conference on tools with artificial intelligence, pp 825–831

  4. Fernández-Delgado M, Cernadas E, Barro S, Amorim D (2014) Do we need hundreds of classifiers to solve real world classification problems? J Mach Learn Res 15(1):3133–3181

    MathSciNet  MATH  Google Scholar 

  5. Fu AM, Dong CR, Wang LS (2015) An experimental study on stability and generalization of extreme learning machines. Int J Mach Learn Cybern 6:1

    Article  Google Scholar 

  6. Fu AM, Wang XZ, He YL, Wang LS (2014) A study on residence error of training an extreme learning machine and its application to evolutionary algorithms. Neurocomputing 146:75–82

    Article  Google Scholar 

  7. Han F, Yao HF, Ling QH (2013) An improved evolutionary extreme learning machine based on particle swarm optimization. Neurocomputing 116:87–93

    Article  Google Scholar 

  8. Hu J, Heidari AA, Shou Y, Ye H, Wang L, Huang X, Wu P (2022) Detection of COVID-19 severity using blood gas analysis parameters and Harris hawks optimized extreme learning machine. Comput Biol Med 142:105166

    Article  Google Scholar 

  9. Huang GB, Chen L, Siew CK (2006) Universal approximation using incremental constructive feedforward networks with random hidden nodes. IEEE Trans Neural Netw 17(4):879–892

    Article  Google Scholar 

  10. Huang GB, Wang DH, Lan Y (2011) Extreme learning machines: a survey. Int J Mach Learn Cybern 2(2):107–122

    Article  Google Scholar 

  11. Huang GB, Zhou HM, Ding XJ, Zhang R (2012) Extreme learning machine for regression and multiclass classification. IEEE Trans Syst Man Cybern B Cybern 42(2):513–529

    Article  Google Scholar 

  12. Huang GB, Zhu QY, Siew CK (2004) Extreme learning machine: a new learning scheme of feedforward neural networks. Proc Int Joint Conf Neural Netw 2:985–990

    Google Scholar 

  13. Huang GB, Zhu QY, Siew CK (2006) Extreme learning machine: theory and applications. Neurocomputing 70(1):489–501

    Article  Google Scholar 

  14. Iosifidis A, Tefas A, Pitas I (2015) On the kernel extreme learning machine classifier. Pattern Recogn Lett 54:11–17

    Article  Google Scholar 

  15. Kasun LLC, Zhou H, Huang GB et al (2013) Representational learning with ELMs for big data. IEEE Intell Syst 28(6):31–34

    Google Scholar 

  16. Lan Y, Soh YC, Huang GB (2009) Ensemble of online sequential extreme learning machine. Neurocomputing 72(13–15):3391–3395

    Article  Google Scholar 

  17. Larrea M, Porto A, Irigoyen E et al (2021) Extreme learning machine ensemble model for time series forecasting boosted by PSO: application to an electric consumption problem. Neurocomputing 452:465–472

    Article  Google Scholar 

  18. Lichman M (2013) UCI machine learning repository. University of California, School of Information and Computer Science, Irvine, CA

  19. Liu N, Wang H (2010) Ensemble based extreme learning machine. IEEE Signal Process Lett 17(8):754–757

    Article  Google Scholar 

  20. Lukasik M, Bontcheva K, Cohn T et al (2019) Gaussian processes for rumour stance classification in social media. ACM Trans Inf Syst 37(2):1–24

    Article  Google Scholar 

  21. Luo JH, Vong CM, Wong PK (2014) Sparse Bayesian extreme learning machine for multi-classification. IEEE Trans Neural Netw Learn Syst 25(4):836–843

    Article  Google Scholar 

  22. Mair S, Brefeld U (2018) Distributed robust Gaussian process regression. Knowl Inf Syst 55(2):415–435

    Article  Google Scholar 

  23. Nguyen V, Gupta S, Rana S, Li C, Venkatesh S (2019) Filtering Bayesian optimization approach in weakly specified search space. Knowl Inf Syst 60(1):385–413

    Article  Google Scholar 

  24. Peng X, Song R, Cao Q, Li Y, Cui D, Jia X, Lin Z, Huang GB (2022) Real-time illegal parking detection algorithm in urban environments. IEEE Trans Intel Transp Syst. https://doi.org/10.1109/TITS.2022.3180225

    Article  Google Scholar 

  25. Rasmussen CE, Williams CKI (2006) Gaussian processes for machine learning. The MIT Press

  26. Silva DNG, Pacifico LDS, Ludermir TB (2011) An evolutionary extreme learning machine based on group search optimization, In: Proceedings of the IEEE congress on evolutionary computation, pp 574–580

  27. Song G, Dai Q, Han X, Guo L (2020) Two novel ELM-based stacking deep models focused on image recognition. Appl Intel 50(5):1345–1366

    Article  Google Scholar 

  28. Soria-Olivas E, Gomez-Sanchis J, Jarman IH, Vila-Frances J (2011) BELM: Bayesian extreme learning machine. IEEE Trans Neural Netw 22(3):505–509

    Article  Google Scholar 

  29. Wang YG, Cao FL, Yuan YB (2011) A study on effectiveness of extreme learning machine. Neurocomputing 74(16):2483–2490

    Article  Google Scholar 

  30. Wilson AG, Adams RP (2013) Gaussian process kernels for pattern discovery and extrapolation. Proc Int Conf Mach Learn 3:1067–1075

    Google Scholar 

  31. Xue J, Zhou S, Liu Q, Liu X, Yin J (2018) Financial time series prediction using \(l\)2, 1RF-ELM. Neurocomputing 277:176–186

    Article  Google Scholar 

  32. Xue XW, Yao M, Wu ZH, Yang JH (2014) Genetic ensemble of extreme learning machine. Neurocomputing 129:175–184

    Article  Google Scholar 

  33. Zhai JH, Xu HY, Wang XZ (2012) Dynamic ensemble extreme learning machine based on sample entropy. Soft Comput 16(9):1493–1502

    Article  Google Scholar 

  34. Zhu QY, Qin AK, Suganthan PN, Huang GB (2005) Evolutionary extreme learning machine. Pattern Recogn 38(10):1759–1763

    Article  MATH  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the editors and three anonymous reviewers whose meticulous readings and valuable suggestions have helped to improve the paper significantly after two rounds of review. This paper was supported by National Natural Science Foundation of China (61972261), Natural Science Foundation of Guangdong Province (2314050006683), Key Basic Research Foundation of Shenzhen (JCYJ20220818100205012), and Basic Research Foundations of Shenzhen (JCYJ20210324093609026, JCYJ20200813091134001).

Author information

Authors and Affiliations

  1. Guangdong Laboratory of Artificial Intelligence and Digital Economy (SZ), Shenzhen, 518107, China

    Xuan Ye, Yulin He, Manjing Zhang & Joshua Zhexue Huang

  2. College of Computer Science & Software Engineering, Shenzhen University, Shenzhen, 518060, China

    Yulin He, Philippe Fournier-Viger & Joshua Zhexue Huang

Authors
  1. Xuan Ye
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yulin He
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Manjing Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Philippe Fournier-Viger
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Joshua Zhexue Huang
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

Data Curation, Writing-Review and Editing, XY; Methodology, Writing-Original Draft Preparation, Writing-Review and Editing, YH; Formal Analysis, Writing-Review and Editing, MZ; Investigation, Writing-Review and Editing, PF-V; Supervision, Funding acquisition, JZH.

Corresponding author

Correspondence to Yulin He.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ye, X., He, Y., Zhang, M. et al. A novel correlation Gaussian process regression-based extreme learning machine. Knowl Inf Syst 65, 2017–2042 (2023). https://doi.org/10.1007/s10115-022-01803-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10115-022-01803-4

Keywords