Abstract
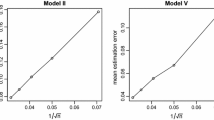
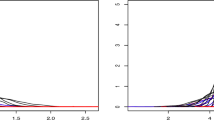
Many sufficient dimension reduction methods for univariate regression have been extended to multivariate regression. Sliced average variance estimation (SAVE) has the potential to recover more reductive information and recent development enables us to test the dimension and predictor effects with distributions commonly used in the literature. In this paper, we aim to extend the functionality of the SAVE to multivariate regression. Toward the goal, we propose three new methods. Numerical studies and real data analysis demonstrate that the proposed methods perform well.
Similar content being viewed by others
References
Aragon Y (1997) A gauss implementation of multivariate sliced inverse regression. Comput Statist 12: 355–372
Chiaromonte F, Cook RD, Li B (2002) Sufficient dimension reduction in regressions with categorical predictors. Ann Statist 30: 475–497
Cook RD (1998) Regression graphics : ideas for studying regressions through graphics. Wiley, New York
Cook RD (2003) Dimension reduction and graphical exploration in regression including survival analysis. Stat Med 22: 1399–1413
Cook RD, Weisberg S (1991) Discussion of a paper by K. C. Li. J Amer Statist Assoc 86: 328–332
Hsing T (1999) Nearest-neighborhood inverse regression. Ann Statist 27: 697–731
Li B, Wen S, Zhu L (2008) On a projective resampling method for dimension reduction with multivariate responses. J Amer Statist Assoc 103: 1177–1186
Li KC (1991) Sliced inverse regression for dimension reduction. J Amer Statist Assoc 86: 316–342
Li KC, Aragon Y, Shedden K, Agnan CT (2003) Dimension reduction for multivariate response data. J Amer Statist Assoc 98: 99–109
Li Y, Zhu L (2007) Asymptotics for sliced average variance estimation. Ann Statist 35: 41–69
Schwarz G. (1978) Estimating the dimension of a model. Ann Math Statist 30: 461–464
Setodji CM, Cook RD (2004) K-means inverse regression. Technometrics 46: 421–429
Shao Y, Cook RD, Weisberg S (2007) Marginal tests with sliced average variance estimation. Biometrika 94: 285–296
Yin X, Bura E (2006) Moment-based dimension reduction for multivariate response regression. J Statist Plann Inference 136: 3675–3688
Yin X, Seymour L (2005) Asymptotic distributions for dimension reduction in the SIR-II method. Statistica Sinica 15: 1069–1079
Yoo JK, Cook RD (2007) Optimal sufficient dimension reduction for the conditional mean in multivariate regression. Biometrika 94: 231–242
Yoo JK (2008a) A novel moment-based dimension reduction approach in multivariate regression. Comput Statist Data Anal 52: 3843–3851
Yoo JK (2008b) Sufficient dimension reduction for the conditional mean in multivariate regression with categorical predictors. J Multivariate Anal 99: 1825–1839
Zhu L, Zhu L (2007) On kernel method for sliced average variance estimation. J Multivariate Anal 98: 970–991
Zhu L, Zhu L, Li X (2007) Transformed partial seast squares for multivariate data. Statistica Sinica 17: 1657–1676
Author information
Authors and Affiliations
Corresponding author
Additional information
The views expressed in this paper are the author own but do not necessarily represent the views of Fannie Mae.
Rights and permissions
About this article
Cite this article
Yoo, J.K., Lee, K. & Wu, S. On the extension of sliced average variance estimation to multivariate regression. Stat Methods Appl 19, 529–540 (2010). https://doi.org/10.1007/s10260-010-0145-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10260-010-0145-9