Abstract
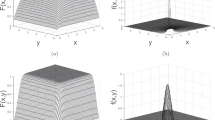
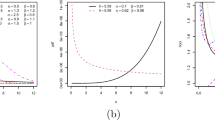
The Gumbel distribution is perhaps the most widely applied statistical distribution for problems in engineering. We propose a generalization—referred to as the Kumaraswamy Gumbel distribution—and provide a comprehensive treatment of its structural properties. We obtain the analytical shapes of the density and hazard rate functions. We calculate explicit expressions for the moments and generating function. The variation of the skewness and kurtosis measures is examined and the asymptotic distribution of the extreme values is investigated. Explicit expressions are also derived for the moments of order statistics. The methods of maximum likelihood and parametric bootstrap and a Bayesian procedure are proposed for estimating the model parameters. We obtain the expected information matrix. An application of the new model to a real dataset illustrates the potentiality of the proposed model. Two bivariate generalizations of the model are proposed.
Similar content being viewed by others
References
Andrade NLR, Moura RMP, Silveira A (2007) Determinação da Q7,10 para o Rio Cuiabá, Mato Grosso, Brasil e comparação com a vazão regularizada após a implantação do reservatório de aproveitamento múltiplo de manso. 24º Congresso Brasileiro de Engenharia Sanitária e Ambiental. Belo Horizonte, Minas Gerais Brasil.
Barakat HM, Abdelkader YH (2004) Computing the moments of order statistic from nonidentically random variables. Stat Methods Appl 13: 15–26
Chen G, Balakrishnan N (1995) A general purpose approximate goodness-of-fit test. J Qual Technol 27: 154–161
Cordeiro GM, de Castro M (2011) A new family of generalized distributions. J Stat Comput Simul 81: 883–898
Cordeiro GM, Ortega EMM, Nadarajah S (2010) The Kumaraswamy Weibull distribution with application to failure data. J Frankl Inst 347: 1399–1429
Cowles MK, Carlin BP (1996) Markov chain Monte Carlo convergence diagnostics: a comparative review. J Am Stat Assoc 91: 133–169
Davison AC, Hinkley DV (1997) Bootstrap methods and their application. Cambridge University Press, New York
DiCiccio TJ, Efron B (1996) Bootstrap confidence intervals. Stat Sci 11: 189–228
Doornik JA (2007) An object-oriented matrix language Ox 5. Timberlake Consultants Press, London
Efron B (1979) Bootstrap methods: another look at the jackknife. Ann Stat 7: 1–26
Efron B, Tibshirani RJ (1993) An introduction to the bootstrap. Chapman and Hall, New York
Eugene N, Lee C, Famoye F (2002) Beta-normal distribution and its applications. Commun Stat Theory Methods 31: 497–512
Fletcher SC, Ponnambalam K (1996) Estimation of reservoir yield and storage distribution using moments analysis. J Hydrol 182: 259–275
Ganji A, Ponnambalam K, Khalili D (2006) Grain yield reliability analysis with crop water demand uncertainty. Stoch Environ Res Risk Assess 20: 259–277
Gelman A, Rubin DB (1992) Inference from iterative simulation using multiple sequences (with discussion). Stat Sci 7: 457–472
Hosking JRM (1990) L-moments: analysis and estimation of distributions using linear combinations of order statistics. J R Stat Soc B 52: 105–124
Jones MC (2004) Families of distributions arising from distributions of order statistics (with discussion). Test 13: 1–43
Jones MC (2009) Kumaraswamy’s distribution: a beta-type distribution with some tractability advantages. Stat Methodol 6: 70–91
Kotz S, Nadarajah S (2000) Extreme value distributions: theory and applications. Imperial College Press, London
Koutsoyiannis D, Xanthopoulos T (1989) On the parametric approach to unit hydrograph identification. Water Resour Manag 3: 107–128
Kumaraswamy P (1980) Generalized probability density-function for double-bounded random-processes. J Hydrol 46: 79–88
Leadbetter MR, Lindgren G, Rootzén H (1987) Extremes and related properties of random sequences and process. Springer, New York
Nadarajah S (2008) On the distribution of Kumaraswamy. J Hydrol 348: 568–569
Nadarajah S, Kotz S (2004) The beta Gumbel distribution. Math Probl Eng 4: 323–332
Ponnambalam K, Seifi A, Vlach J (2001) Probabilistic design of systems with general distributions of parameters. Int J Circuit Theory Appl 29: 527–536
Prudnikov AP, Brychkov YA, Marichev OI (1986) Integrals and series, vols 1, 2 and 3. Gordon and Breach Science Publishers, Amsterdam
Seifi A, Ponnambalam K, Vlach J (2000) Maximization of manufacturing yield of systems with arbitrary distributions of component values. Ann Oper Res 99: 373–383
Sundar V, Subbiah K (1989) Application of double bounded probability density-function for analysis of ocean waves. Ocean Eng 16: 193–200
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Cordeiro, G.M., Nadarajah, S. & Ortega, E.M.M. The Kumaraswamy Gumbel distribution. Stat Methods Appl 21, 139–168 (2012). https://doi.org/10.1007/s10260-011-0183-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10260-011-0183-y