Abstract
The near-lossless compression technique has better compression ratio than lossless compression technique while maintaining a maximum error limit for each pixel. It takes the advantage of both the lossy and lossless compression methods providing high compression ratio, which can be used for medical images while preserving diagnostic information. The proposed algorithm uses a resolution and modality independent threshold-based predictor, optimal quantization (q) level, and adaptive block size encoding. The proposed method employs resolution independent gradient edge detector (RIGED) for removing inter-pixel redundancy and block adaptive arithmetic encoding (BAAE) is used after quantization to remove coding redundancy. Quantizer with an optimum q level is used to implement the proposed method for high compression efficiency and for the better quality of the recovered images. The proposed method is implemented on volumetric 8-bit and 16-bit standard medical images and also validated on real time 16-bit-depth images collected from government hospitals. The results show the proposed algorithm yields a high coding performance with BPP of 1.37 and produces high peak signal-to-noise ratio (PSNR) of 51.35 dB for 8-bit-depth image dataset as compared with other near-lossless compression. The average BPP values of 3.411 and 2.609 are obtained by the proposed technique for 16-bit standard medical image dataset and real-time medical dataset respectively with maintained image quality. The improved near-lossless predictive coding technique achieves high compression ratio without losing diagnostic information from the image.
Electronic supplementary material
The online version of this article (10.1007/s10278-019-00283-3) contains supplementary material, which is available to authorized users.
Keywords: Near-lossless compression, Quantizer, Gradient edge detector, Arithmetic encoding, Entropy coding
Introduction
Tremendous amounts of medical image data are generated in biomedical imaging field, especially volumetric MRI and CT scan having stack of 2D image slices. All the generated image data is stored in digital form and this large amount of data requires efficient storage and transmission [1]. It is very difficult for a hospital to store such abundance of data and this large amount of data requires large bandwidth for transmission purpose. To deal with these issues, compression of medical image data is required. Lossless compression techniques are traditionally preferred for medical images to avoid false diagnosis, although the compression ratio (CR) achieved is quite low, ranging from 2 to 4 depending upon the employed methods [2]. Lossy compression is an irreversible technique for image compression, which provides good compression efficiency but degrades the image quality. This type of technique is not acceptable for medical images as little degradation of critical diagnostic information may lead to wrong diagnosis, which is a major issue for radiologist. However, to obtain high CR, some distortion is allowed in the recovered image as reported by many researchers in medical image compression community [3]. Lossy image compression is justified only if critically diagnostic region is maintained with very little distortion to ensure better quality of the compressed image [4]. Near-lossless compression limits the maximum error for every pixel to a given specified value. Near-lossless compression potentially increases compression efficiency and utilizes less bandwidth while saving the diagnostic information of the medical image. In addition to telemedicine application in medical field, near-lossless coding techniques would be useful in remote sensing applications.
In literature, different compression techniques are available such as dictionary encoding, transformation encoding, and predictive encoding technique. Compression performance achieved by transform-based coding is not high and the most admired method used in near-lossless system is the prediction-based coding method, such as differential pulse code modulation (DPCM) [5]. To compress the still images, JPEG2000 is a new standard [6, 7]. JPEG and JPEG2000 using DCT and DWT respectively are transform-based standards. JPEG 2000 provides superior compression and supports features such as lossy to lossless coding and resolution scalability [8].
The newest international JPEG standard for near-lossless and lossless coding is JPEG-LS having low computational complexity [9]. A low-cost and computational complexity rate control algorithm is proposed by Jiang & Grecos that is useful for comprehensive and other extensive applications. The results indicate that the rate control JPEG-LS is effective in terms of quality parameters [9]. Caldelli et al. [10, 11] used JPEG-LS for designing a near-lossless system employed for telemedicine applications. Ayinde proposed a near-lossless image compression-decompression using zipper transformation (ZT) and inverse zipper transformation (IZT). Numerical simulations are done showing ZT-based compression algorithm provides faster implementation than DCT. Natural and medical image database is used for performance evaluation. It is reported that the proposed method outperform the DCT-based methods in compressing image data [12]. To enhance the compression performance, a source model with multiple contexts and arithmetic coding is proposed by Chen & Ramabadran. Several MR and US (Ultrasound) images are used for experiment showing the DPCM can provide the CR in the range of 4 to 10 with high PSNR value of about 50 dB for 8-bit-depth medical image datasets [4]. Khobragade and Thakare proposed a hybrid lossless image compression technique making use of DWT and DCT with better compression in transform domain [13]. A two-stage near-lossless coding method for hyperspectral image datasets is proposed by Beerten et al. and this technique includes a near-lossless and lossy layer. Experimental results demonstrate that the coding performance of this two-stage near-lossless method is highly efficient for hyperspectral images and outperform JPEG-2000 and M-CALIC [14]. Song et al. proposed an adaptive spatial prediction based on near-lossless coding algorithm for volumetric medical image datasets. The blocks are predicted in the spatial domain directly by using adaptive block size prediction. Before quantization, lossless Hadamard transform is used to improve the quality of recovered medical images. Volumetric 8-bit CT and MRI database are used for evaluation of the proposed technique. The experimental results indicate that the medical images are efficiently compressed by the proposed algorithm and provide better quality in terms PSNR than the other near-lossless approaches [2]. Boopathiraja and Kalavathi proposed a near-lossless coding technique for multispectral images and the wavelet transformation is employed with Huffman encoder to encode the image efficiently. Results of this technique show that space complexity is better removed by this technique and it is better applicable in satellite imaging [15]. Zhang and Xiaolin proposed a new design of the network for image compression after identifying a major weakness of the previously existing. This research work in a new neural network paradigm of image compression is suitable for the applications of precision machine vision in the near-lossless image decompression [16]. Simić et al. proposed a coding method using Hadamard transform and vector quantization for grayscale images. A simple generalized algorithm for vector quantization and segmentation algorithm is proposed by the author. The performance of new algorithm is compared with the existing methods in which linear prediction and dual mode quantization is done. The gain of 6.95 (dB) is achieved by the proposed technique and also required less processing time [17]. Bartrina-Rapesta et al. proposed a rate control algorithm for image compression based on predictive coding technique to yield the high quality of the recovered image [18]. The performance of this technique is better than the latest predictive image coding system [19] and JPEG2000 in terms of quality peak absolute error (PAE).
Problem Formulation
High compression ratio is achieved by the lossy compression method and error-free recovery of image is achieved by the lossless method. Near-lossless compression method takes the advantage from both the compression methods providing high compression ratio with pixelwise image quality control. The maximum error in every pixel is limited by a specified value in the near-lossless compression. The determination of optimal quantization (q) level and maximum tolerable distortion in recovered image in near-lossless compression technique is an open research challenge and has not been addressed in the literature. The selection of the quality parameters for assessing the optimal q level at which high compression ratio can be achieved with maintained quality of image is also a point of concern.
Contribution
Addressing the previous stated problems, this research work contributes a novel effective near-lossless coding method providing high coding efficiency. The proposed near-lossless method is based on the predictive coding method employing RIGED with optimal threshold value [20, 21] for prediction, quantizer with optimal q level, and BAAE [22] with optimal block size for encoding. RIGED provides efficient prediction of the image results in less entropy valued residual image and BAAE offers optimal block size for encoding. Optimal value of q level is chosen after quantitative and qualitative analysis, which finally provides high-quality recovered image with high coding efficiency. The validity of choice of a q level is done by the radiologist from the Govt. Ripon Hospital, Distt. Shimla (H.P).
The remainder of the paper is organized as follows. The background theory of prediction-based compression technique is provided in the “Background Theory” section. The proposed method for near-lossless image compression is presented in the “The Proposed Method” section. The “Experimentation Details” section includes the brief description of dataset details and the performance parameters used for assessment of the proposed technique. Results are provided in the “Results and Discussion” section. Finally, the “Conclusion” section presents the conclusion of the paper.
Background Theory
Predictive Coding Technique
Pixel value prediction of an image is an essential part of predictive coding, because it reduces the spatial redundancy from the image. Every pixel prediction is done individually from a context (a group of neighboring pixels) in the order of raster scan. Prediction error image or residual is obtained by subtracting predicted image from an original image. The residual is lower entropy valued as compared with the original medical image [23].
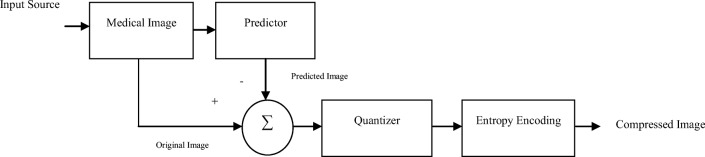
Basic schematic diagram of prediction compression scheme is given in Fig. 1.
Fig. 1.
Basic schematic diagram of predictive coding algorithm
Predictor
Predictor removes the inter-pixel redundancy from the volumetric medical images operating in a slice-by-slice basis. The selection of highly efficient predictor is essential for the coding efficiency of the compression method. Predictor’s efficiency depends on how well it can reduce the entropy of the prediction error, which in turn depends on the predictor’s accuracy. Lowering the residual image’s entropy better will be the predictor’s performance, which results in better compression.
Gradient adaptive predictor (GAP) and median edge detector (MED) are two standard predictors for prediction [24]. MED is computationally less complex as compared with GAP, whereas the latter is more accurate. Combination of these two predictors is gradient edge detection (GED), which takes advantage of computational efficiency and prediction accuracy from MED and GAP respectively [25]. GED is threshold-based predictor and it selects one threshold for prediction that is user defined.
Quantization
An original data is represented by a minimum loss of information with a good quantizer [26]. It is a lossy process and compression is achieved when range of values is compressed into a single-quantum value. Some distortion and loss of bits is allowed in the medical image if there is no diagnostic information loss in the recovered image and the near-lossless compression limits the maximum error for every pixel to a given specified value.
Entropy Encoding
Entropy encoding is used to remove statistical redundancy. Different encoding techniques such as Huffman, run-length, dictionary, arithmetic, and bit-plane coding are reported in literature. Among other entropy encoding techniques, arithmetic encoding is an efficient coding technique [27]. This coding technique does not separate the input symbol into component symbols, but encodes the entire message into a single-bit stream. Fewer numbers of bits are required to encode frequently occurring characters and infrequent characters are stored with the more number of bits resulting in fewer bits in total.
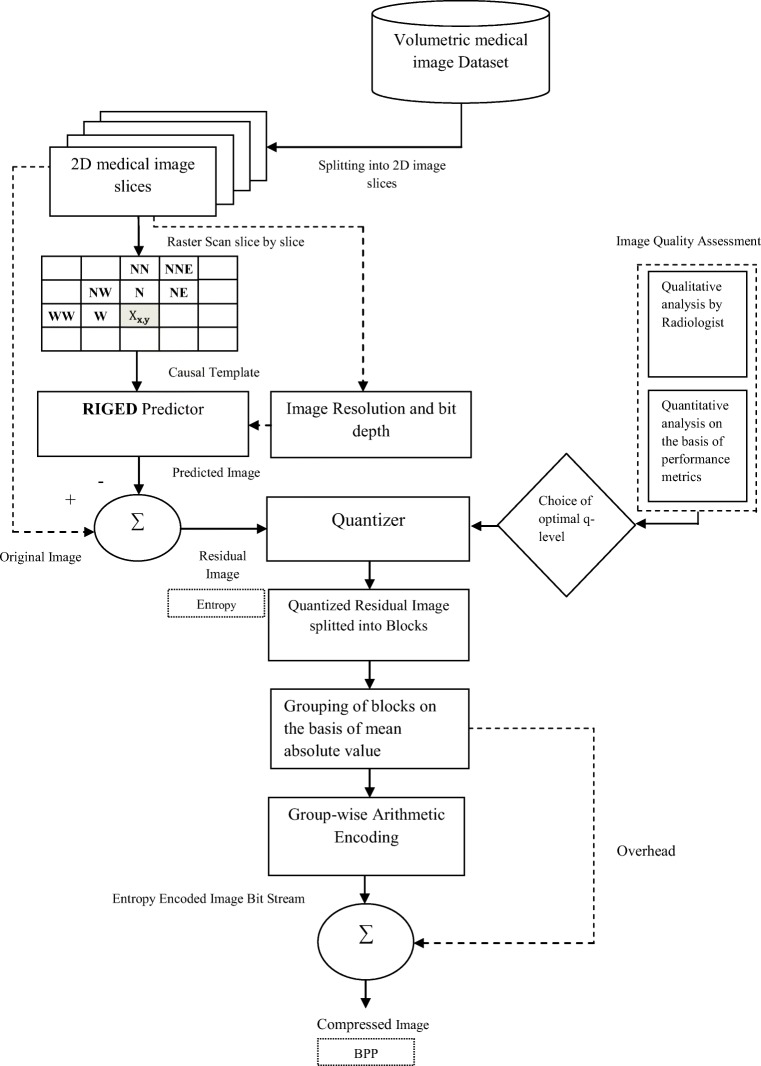
The Proposed Method
Pixel prediction, quantization, and entropy encoding are three main steps of the proposed near-lossless predictive coding technique. A schematic diagram of the proposed technique is represented in Fig. 2.
Fig. 2.
Proposed near-lossless predictive coding algorithm
The null hypothesis:
Ho: The quantization of image introduces an irreversible error, which in turn adversely affects the image quality and its diagnostic capability by the radiologist.
H1: The null hypothesis rejected.
Novelty of the proposed algorithm is to design an improved near-lossless predictive coding technique with the optimal threshold value, optimal q level, and the block-based coding that removes inter-pixel, psychovisual, and coding redundancy to achieve high compression without losing diagnostic information from the medical image. Step I includes the prediction for removing spatial or inter-pixel redundancy from the image. In step II, prediction error image or residual obtained after prediction is quantized at optimal q level for removing psychovisual redundancy. Step III includes encoding of quantized residual after breaking into small blocks for removing coding redundancy from the image.
Resolution Independent Gradient Edge Detector
GED is a threshold-based predictor and a particular threshold value should be selected to minimize the entropy of the residual image for perfect prediction. In literature, there is no specific method for threshold value selection of GED prediction.
RIGED removes the demerit of GED and is designed to make GED predictor resolution independent that specifies the optimal value of the threshold for prediction. From the extensive experiments conducted on the medical image datasets of varying modalities and varying resolution, optimal threshold value is selected empirically [20, 21]. Residual image E (x,y) resulting from RIGED has minimum entropy value that requires lesser number of bits for encoding. RIGED algorithm is designed for medical images having bit depth of 8 and 16 bits. Threshold level for medical images can be up to 2-bit depth. The algorithm of this RIGED model is given in Eq. (1).
| 1 |
Inter-pixel redundancy from the image is better removed by RIGED, in which the minimum value of entropy is obtained at the threshold of 44 for 8-bit medical images and 768 for 16-bit medical images after exhaustive experiments done by the author [25].
Optimum q Level Quantization
Residual image E (x,y) obtained by subtracting predicted image X̅ (x,y) from the original image X (x,y) using RIGED predictor has less entropy value. Quantization of E (x,y) can be done at different levels (q levels). Qualitative and quantitative analysis of proposed technique is done at different q levels to obtain an optimal value providing quantized image with minimum loss of information and high compression.
Qualitative analysis is done on the basis of subjective image quality assessment which depends upon detection and estimation tasks. Detection is the very common task that based on the presence and absence of pathology analysis. Estimation is the other important task that gives diagnosis criteria quality [28]. Qualitative analysis of quantized residual images at different q levels for a choice of optimal q level was done by the radiologist at the Govt. Ripon Hospital, Distt. Shimla. Quantitative analysis of the quantized residual at different q levels was done on the basis of different performance parameters. After qualitative and quantitative analysis, optimal value of q level selected which is used to compress the original image data without the loss of diagnostic information.
Residual and quantized residual is given by Eqs. (2) and (3).
| 2 |
| 3 |
where q is the quantization level.
Block Adaptive Arithmetic Encoding
The third main step in the proposed near-lossless predictive coding technique is encoding which encode the prediction error image that provides compression in terms of BPP. After quantizing at optimal q level, a block-based arithmetic encoding is done for efficient compression of medical images. In different image regions, there are different error probabilities so the quantized prediction error image obtained after RIGED is divided into blocks before applying arithmetic encoder. Image segmentation is done in fixed size blocks of 8 × 8 [22], as it is optimal block size obtained after empirical analysis providing minimum bit rate of compressed image. Classification of blocks is done into different groups on the mean absolute error basis. Each group is encoded by arithmetic encoder separately. Overhead (side information) of the blocks is essential at decoder side for image decompression.
Experimentation Details
Dataset Used
The proposed algorithm was tested on 8- and 16-bit CT and MRI medical image sequences collected from four different sources. The algorithm is implemented in MATLAB. The test set I is a standard database which contains 8-bit CT and MR images having resolutions of 256 × 256 and 512 × 512 presented in Table 1. These datasets are collected from CIPR and MRI images from the Computer Vision Group [29] at the University of Granada. Table 2 gives description of test set II and contains 16 bits of standard CT and MR images. The raw images of CT and MR sequence images contained in test set III are detailed in Table 3. Medical images in Table 2 are belonging to the Cancer Imaging Archive [30]. The test set III presented in Table 3, collected from local hospitals: Banga’s Diagnostic Center placed in Distt. Mandi (H.P) and Govt. Indira Gandhi Medical College (IGMC) Distt. Shimla (H.P), India, includes MR and CT image sets respectively.
Table 1.
Test set I is standard dataset composed of 8-bit CT and MR images
| Sequence name | Image size (rows × columns × slices) | Bits |
|---|---|---|
| CT-Aperts | 256 × 256 × 97 | 6,356,992 |
| CT-carotid | 256 × 256 × 74 | 4,849,664 |
| CT-skull | 256 × 256 × 203 | 13,303,808 |
| CT-wrist | 256 × 256 × 183 | 11,993,088 |
| MR-liver-T1 | 256 × 256 × 58 | 3,801,088 |
| MR-liver-T2e1 | 256 × 256 × 58 | 3,801,088 |
| MER-ped-chest | 256 × 256 × 77 | 5,046,272 |
| MR-sag-head | 256 × 256 × 58 | 3,801,088 |
| MR-Brain | 256 × 256 × 16 | 1,048,576 |
Table 2.
Test set II is standard dataset composed of 16-bit medical images of different resolutions
Table 3.
Test set III collected from local hospitals contains 16-bit CT and MR images of different resolutions
| Sequence name | Image size (rows × columns × slices) | Bits |
|---|---|---|
| MR_1 | 512 × 512 × 12 | 31,455,728 |
| MR_2 | 512 × 512 × 20 | 5,242,880 |
| MR_3 | 256 × 512 × 11 | 720,896 |
| MR_4 | 512 × 512 × 20 | 5,242,880 |
| MR_5 | 512 × 512 × 20 | 5,242,880 |
| MR_6 | 256 × 256 × 40 | 2,621,440 |
| CT_1 | 512 × 512 × 32 | 8,388,608 |
| CT_2 | 512 × 512 × 63 | 16,515,072 |
| CT_3 | 512 × 512 × 249 | 65,273,856 |
Performance Parameters
Qualitative Parameters
Qualitative analysis of an image is performed by group of specialist who rate the visual quality of the image and the quality of diagnostic information present in the image.
Analysis depends on the information extracted from the images, and usually detection and estimation are two main tasks that are to be evaluated. Presence and absence of pathology are analyzed by detection and the diagnosis criteria quality is an assessment of estimation task. These two quality assessment tasks judge the quality of medical images [28].
Quantitative Parameters
Entropy is a quality factor of predictors as the efficiency of the predictor is inversely related to the residual’s entropy [34]. Entropy of residual is calculated after RIGED prediction that can be used for the evaluation of CR.
Image quality is expressed in terms of PSNR and it is directly depend upon mean square error (MSE). The lower the MSE, the higher will the PSNR be, and the better will be the image quality [35]. Universal image quality index (Q) is used as an image distortion measure. It is the combination of correlation, luminance distortion, and contrast distortion. The range of values for the Q index is from − 1 to 1. The predicted image is similar to the original image if Q index approaches to 1. The value approaching towards − 1 shows the dissimilarity between two images. If the images are identical, only then the best value 1 is achieved.
Results and Discussion
The proposed algorithm is tested on 8-bit and 16-bit medical sequence image (CT and MRI). Nine datasets of 8-bit-depth medical images having more than 557 CT and 267 MRI slices were used. Four sets of 16-bit-depth medical images from publically available datasets were used having 135 CT and 236 MRI slices. Nine datasets of 16 bits collected from local hospitals having more than 344 CT and 123 MRI images were used.
In this section, results obtained with the proposed method are discussed. Performance of the proposed technique is analyzed at different q levels after qualitative and quantitative analysis for all datasets given in the “Dataset Used” section. Optimum q level which provides recovered image with negligible loss of information and with high compression is obtained after verified by the radiologist of Govt. Ripon Hospital, Distt. Shimla, H.P. It is also validated on the basis of different performance parameters. Overall compression results of the proposed technique is compared with the results obtained for existing near-lossless compression standards.
Qualitative Analysis of the Proposed Technique
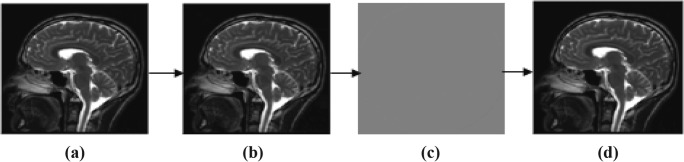
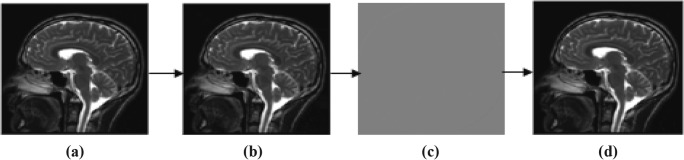
In this subsection, proposed technique is analyzed for compression performance of various volumetric images of 8- and 16-bit depth. Original image is initially predicted by RIGED at optimal threshold value for efficient prediction that provides minimum entropy of residual images. Residual image is quantized and recovered at different q levels of 2, 4, 6, 8, 10, 12, 14, 16, 18, and 20. One of the image samples with minimum and maximum distorted q level is shown in Fig. 3. MRI original image sample, predicted images, residual images, and recovered images at q = 2 and q = 20 are shown in Figs. 3 and 4.
Fig. 3.
Sample of MRI at (q = 2). a Original image. b Predicted image. c Residual image. d Recovered image (q = 2)
Fig. 4.
Sample of MRI at (q = 20). a Original image. b Predicted image. c Residual image. d Recovered image
Validation of Processed Images by Radiologist
For the near-lossless techniques, as the q level increases, the quality decreases rapidly. Quantization (q) level is always set to be small to meet the requirements of recovered image quality as medical images maintain the high quality along with high CR. Images recovered at different q levels and validated by the radiologist for optimum value of q level at which the image is recovered without any loss of diagnostic information. Subjective quality assessment of MRI and CT image samples of varying bit depth is verified by radiologists at different q levels are given in Tables 4 and 5. The radiologist rates the diagnosis as well as visual quality of an image and observes all the necessary details. Depending upon the task that is to be evaluated, image assessment methods are selected. Detection and estimation are two different tasks that are generally used for assessment purpose. Overall visual quality of the image is assessed on the scale of 1 to 5 (1, unaceptable; 2, poor; 3, satisfactory; 4, good; and 5, excellent) by the radiologist.
Table 4.
Image quality assessment of MR image samples from radiologists
| Image quality assessment | |||||||
|---|---|---|---|---|---|---|---|
| MRI_16-bit image sample | Detection | Estimation | Overall performance | MRI_8-bit image sample | Detection | Estimation | Overall performance |
| MR_16_01 | ✓ | ✓ | 5 | MR_8_01 | ✓ | ✓ | 5 |
| MR_16_02 | ✓ | ✓ | 5 | MR_8_02 | ✓ | ✓ | 5 |
| MR_16_03 | ✓ | ✓ | 5 | MR_8_03 | ✓ | ✓ | 5 |
| MR_16_04 | ✓ | ✓ | 5 | MR_8_04 | ✓ | ✓ | 5 |
| MR_16_05 | ✓ | ✓ | 5 | MR_8_05 | ✓ | ✓ | 5 |
| MR_16_06 | ✓ | ✓ | 5 | MR_8_06 | ✓ | ✓ | 5 |
| MR_16_08 | ✓ | ✓ | 5 | MR_8_08 | ✓ | ✓ | 5 |
| MR_16_10 | ✓ | × | 4 | MR_8_10 | ✓ | × | 4 |
| MR_16_12 | ✓ | × | 4 | MR_8_12 | ✓ | × | 4 |
| MR_16_14 | ✓ | × | 3 | MR_8_14 | ✓ | × | 3 |
| MR_16_16 | ✓ | × | 3 | MR_8_16 | ✓ | × | 3 |
| MR_16_18 | ✓ | × | 2 | MR_8_18 | ✓ | × | 2 |
Table 5.
Image quality assessment of CT image samples from radiologists
| Image quality assessment | |||||||
|---|---|---|---|---|---|---|---|
| CT_16-bit image sample | Detection | Estimation | Overall performance | CT_8-bit image sample | Detection | Estimation | Overall performance |
| CT_16_01 | ✓ | ✓ | 5 | CT_8_01 | ✓ | ✓ | 5 |
| CT_16_02 | ✓ | ✓ | 5 | CT_8_02 | ✓ | ✓ | 5 |
| CT_16_03 | ✓ | ✓ | 5 | CT_8_03 | ✓ | ✓ | 5 |
| CT_16_04 | ✓ | ✓ | 5 | CT_8_04 | ✓ | ✓ | 5 |
| CT_16_05 | ✓ | ✓ | 5 | CT_8_05 | ✓ | ✓ | 5 |
| CT_16_06 | ✓ | ✓ | 5 | CT_8_06 | ✓ | ✓ | 5 |
| CT_16_08 | ✓ | ✓ | 5 | CT_8_08 | ✓ | ✓ | 5 |
| CT_16_10 | ✓ | ✓ | 5 | CT_8_10 | ✓ | ✓ | 5 |
| CT_16_12 | ✓ | × | 4 | CT_8_12 | ✓ | × | 3 |
| CT_16_14 | ✓ | × | 3 | CT_8_14 | ✓ | × | 3 |
| CT_16_16 | ✓ | × | 2 | CT_8_16 | ✓ | × | 2 |
| CT_16_18 | ✓ | × | 2 | CT_8_18 | ✓ | × | 2 |
Reconstructed images with q levels, q = 2 to q = 20, were used for subjective image quality assessment by radiologist. By radiologist’s point of view, q = 8 is an optimal q level at which reconstructed image is visually same as that of original medical image without losing any important diagnostic information. Detection of pathological area of image up to q = 18 (maximum distortion) is acceptable and estimation of pathology is up to q = 8, and for CT image samples, it can be up to q = 10. The chosen q level should be optimal in terms of clarity and reduced distortion of the recovered image. So, in this work, q level of quantization is selected as 8 for all MR and CT image samples, at which recovered images are detected and estimated correctly.
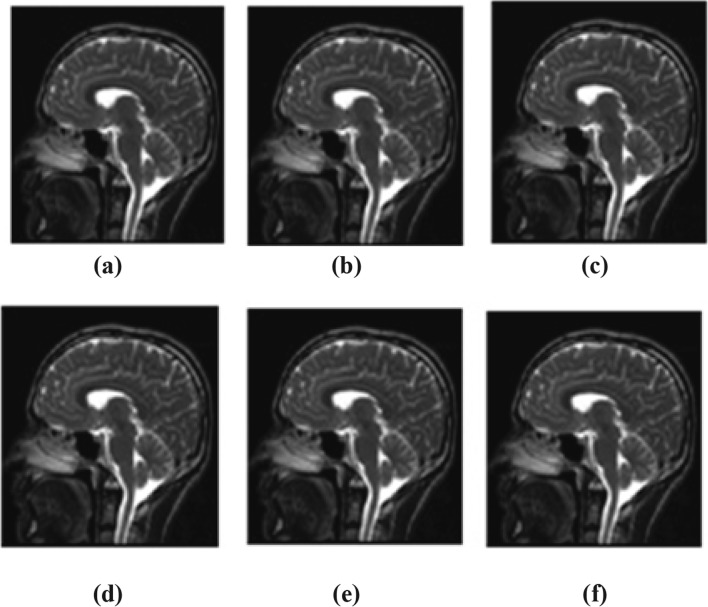
As q = 8 is the optimum q level for exact recovery of an image, recovered images at different q levels are represented visually. Various image samples of different resolution and modalities are recovered at different q levels. Sample reconstructed MRI and CT image is shown in Figs. 5 and 6. Recovered images at q = 2 (minimum distortion), q = 8 (optimal q level), q = 6, 10 (q levels before and after q = 8), and q = 18 (maximum tolerable distortion) are shown in Figs. 5 and 6.
Fig. 5.
Sample recovered images of MRI. a Original image. bq = 2. cq = 6. dq = 8. e q = 10. f = 18
Fig. 6.
Sample recovered images of CT. a Original image. bq = 2. cq = 6. dq = 8. e q = 10. fq = 18
Assessment by radiologist gives a q level of 8 is optimal for diagnosis.
Quantitative Analysis of the Proposed Technique in Terms of Performance Parameters
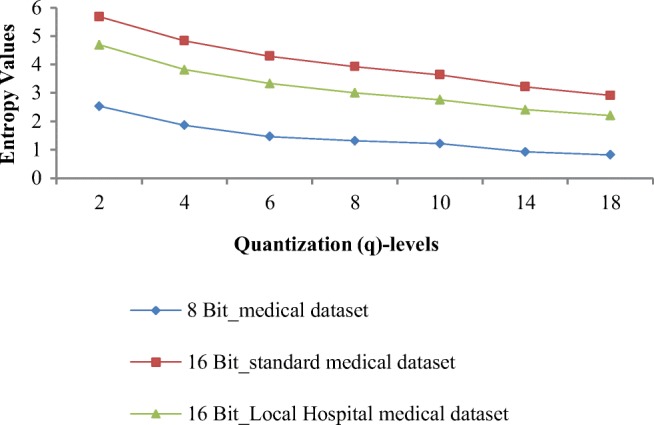
Entropy values of quantized residuals obtained by the proposed technique for different image datasets at varying q levels are shown in Fig. 7. Weighted average entropy values of original image for 8-bit image dataset, 16-bit standard image dataset, and 16-bit local hospital’s image dataset are 4.433, 8.229, and 7.846 respectively. Entropy values of quantized residual obtained at minimum distortion q level (q = 2) is 2.533, 5.688, and 4.697 for 8-bit image dataset, 16-bit standard image dataset, and 16-bit local hospital’s image dataset respectively. As the q level increases, entropy decreases that increases the compression efficiency but quality degrades rapidly.
Fig. 7.
Entropy values obtained by proposed algorithm at varying q levels
At q = 8, entropy values of quantized residuals are 1.313, 3.928, and 3.006 for 8-bit image dataset, 16-bit standard image dataset, and 16-bit local hospital’s image dataset respectively. Overall entropy value achieved at q = 18 is 27.69% less as compared with q = 8. For all three datasets, decrease in entropy value from q = 2 to q = 8 is large and from q = 8 to q = 18, there is very small decrease in entropy value. Overall percentage gap of 36.20% in the entropy value is achieved when q level changes from minimum distorted q level to optimal q level (q = 2 to q = 8).
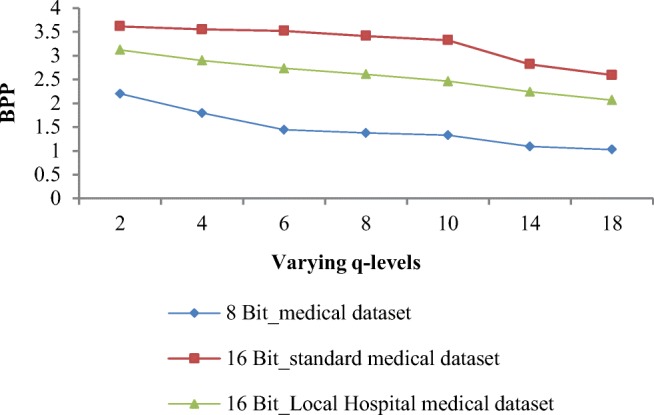
Quantization of predicted residual is followed by block-based arithmetic encoding of residual coefficients. Weighted average of BPP values is calculated for all three medical image datasets at different q levels and depicted in Table 6. BPP values are 2.199, 3.614, and 3.123 for 8-bit image dataset, 16-bit standard image dataset, and 16-bit local hospital’s image dataset respectively at q = 2 and goes on decreasing when q level increases. At optimal q level of 8, BPP values are reduced to 1.373, 3.411, and 2.609 for all three respective datasets; after this, q point distortion is maximum and recovered image is not tolerable for diagnosis. The decreasing trend of BPP is uniform for MRI and CT images for all the datasets. So, after qualitative and quantitative analysis, q = 8 is found as an optimal q level for quantization irrespective of type and resolution of image.
Table 6.
BPP values obtained for all three medical datasets of different bit depths at varying of q-levels
| Medical Image Samples | BPP for various q-Levels | |||||||
|---|---|---|---|---|---|---|---|---|
| q=2 | q=4 | q=6 | q=8 | q=10 | q=14 | q=18 | ||
| 8 Bit Depth Image Dataset (Publically Available Database) | CT_Apert | 1.188 | 1.000 | 0.702 | 0.653 | 0.529 | 0.501 | 0.388 |
| CT_corotid | 1.864 | 1.656 | 1.269 | 1.096 | 1.094 | 0.864 | 0.791 | |
| CT_skull | 2.618 | 2.176 | 1.803 | 1.744 | 1.758 | 1.038 | 1.026 | |
| CT_wrist | 1.813 | 1.478 | 1.218 | 1.107 | 1.098 | 1.012 | 0.980 | |
| MRI_liver_T2 | 2.752 | 2.112 | 1.594 | 1.512 | 1.352 | 1.318 | 1.203 | |
| MRI_Liver_T1 | 2.865 | 2.225 | 1.773 | 1.730 | 1.590 | 1.480 | 1.399 | |
| MRI_chest | 2.165 | 1.910 | 1.679 | 1.663 | 1.626 | 1.660 | 1.560 | |
| MRI_head | 2.700 | 1.975 | 1.659 | 1.642 | 1.561 | 1.530 | 1.400 | |
| Mr_brain | 2.564 | 2.493 | 2.285 | 2.116 | 2.032 | 1.763 | 1.599 | |
| Weighted average | 2.199 | 1.793 | 1.440 | 1.373 | 1.326 | 1.090 | 1.026 | |
| 16 Bit-Depth Image Dataset (Publically Available Database) | Ct_lung_1 | 3.687 | 3.635 | 3.595 | 3.502 | 3.555 | 2.422 | 2.193 |
| CT_LUNG_2 | 3.783 | 3.699 | 3.575 | 3.577 | 3.523 | 3.237 | 2.967 | |
| MR_Breast | 3.419 | 3.376 | 3.307 | 3.250 | 3.208 | 3.095 | 3.082 | |
| MR_Neuro | 3.310 | 3.255 | 3.216 | 3.145 | 3.073 | 2.681 | 2.445 | |
| Weighted average | 3.614 | 3.550 | 3.520 | 3.411 | 3.324 | 2.818 | 2.590 | |
| 16 Bit-Depth Image Dataset (From Govt. Hospital) | MR_1 | 4.290 | 3.472 | 3.026 | 2.729 | 2.510 | 2.166 | 2.031 |
| MR_2 | 4.722 | 3.816 | 3.343 | 3.010 | 2.760 | 2.347 | 2.199 | |
| MR_3 | 5.587 | 4.604 | 4.041 | 3.651 | 3.359 | 2.940 | 2.650 | |
| MR_4 | 4.300 | 3.401 | 2.930 | 2.620 | 2.394 | 2.046 | 1.847 | |
| MR_5 | 3.781 | 2.999 | 2.607 | 2.329 | 2.128 | 1.781 | 1.673 | |
| MR_6 | 5.216 | 4.290 | 3.784 | 3.411 | 3.078 | 2.615 | 2.566 | |
| CT_1 | 4.016 | 3.151 | 2.704 | 2.419 | 2.202 | 1.893 | 1.743 | |
| CT_2 | 6.200 | 5.364 | 4.860 | 4.500 | 4.222 | 3.803 | 3.468 | |
| CT_3 | 4.496 | 3.602 | 3.106 | 2.778 | 2.541 | 2.212 | 2.010 | |
| Weighted average | 3.123 | 2.900 | 2.734 | 2.609 | 2.462 | 2.241 | 2.067 | |
Obtained weighted average of BPP values at varying q levels for three different datasets given in dataset section are graphically shown in Fig. 8. Percentage gap between entropy value when it decreases from q = 2 to q = 8 is 8.36% and q = 8 is maximum q level up to where estimation of image is acceptable for diagnosis.
Fig. 8.
BPP values obtained by proposed algorithm at varying q levels
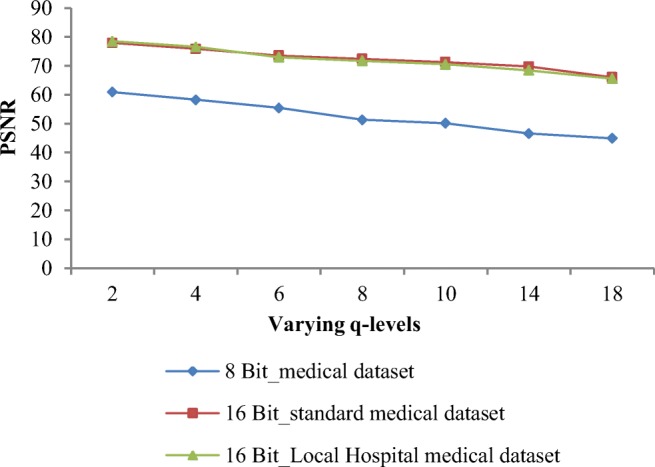
Other quality parameters: PSNR and quality index are also calculated for recovered images. Table 7 gives the PSNR values for different image datasets having varying resolutions at different q levels. As the value of q level increases, the PSNR decreases rapidly. Weighted average of PSNR for 16-bit standard datasets and 16-bit local hospital’s image datasets at q = 8 (maximum tolerable distortion) is 72.4 dB and 71.7 dB respectively, whereas for 8-bit-depth medical dataset, weighted average of PSNR is 51.3 dB.
Table 7.
PSNR values obtained for all three medical datasets of different bit depths at varying of q-levels
| Medical Image Datasets | PSNR for various q-Levels | |||||||
|---|---|---|---|---|---|---|---|---|
| q=2 | q=4 | q=6 | q=8 | q=10 | q=14 | q=18 | ||
| 8 Bit Depth Image Dataset (Publically Available Database) | CT_Apert | 65.237 | 57.220 | 55.793 | 50.487 | 49.202 | 47.720 | 45.122 |
| CT_corotid | 61.611 | 58.092 | 56.402 | 52.704 | 50.736 | 46.090 | 45.413 | |
| CT_skull | 60.468 | 58.117 | 55.272 | 52.185 | 51.201 | 47.744 | 46.108 | |
| CT_wrist | 60.712 | 58.601 | 55.372 | 52.234 | 51.240 | 45.123 | 43.661 | |
| MRI_liver_T2 | 58.113 | 58.041 | 54.418 | 49.467 | 48.422 | 45.738 | 44.919 | |
| MRI_Liver_T1 | 59.011 | 58.693 | 56.832 | 50.104 | 48.423 | 46.844 | 45.154 | |
| MRI_chest | 61.075 | 59.730 | 54.843 | 50.255 | 49.029 | 47.824 | 45.179 | |
| MRI_head | 61.203 | 57.979 | 54.856 | 50.259 | 48.953 | 45.512 | 43.617 | |
| Mr_brain | 59.08 | 53.11 | 49.24 | 47.02 | 46.89 | 44.80 | 43.01 | |
| Weighted average | 60.968 | 58.257 | 55.431 | 51.355 | 50.146 | 46.586 | 44.944 | |
| 16 Bit-Depth Image Dataset (Publically Available Database) | Ct_lung_1 | 79.006 | 77.035 | 75.059 | 73.611 | 72.213 | 70.815 | 66.347 |
| CT_LUNG_2 | 78.848 | 77.245 | 74.398 | 73.801 | 72.637 | 71.544 | 67.298 | |
| MR_Breast | 73.341 | 70.742 | 69.322 | 68.056 | 67.390 | 65.526 | 63.940 | |
| MR_Neuro | 76.415 | 73.876 | 71.347 | 70.046 | 69.169 | 66.720 | 64.456 | |
| Weighted average | 77.925 | 75.906 | 73.542 | 72.440 | 71.298 | 69.733 | 66.065 | |
| 16 Bit-Depth Image Dataset (From Govt. Hospital) | MR_1 | 82.712 | 79.702 | 77.637 | 76.417 | 75.190 | 73.315 | 68.094 |
| MR_2 | 83.319 | 78.695 | 77.139 | 76.201 | 74.631 | 72.079 | 68.377 | |
| MR_3 | 85.916 | 82.016 | 79.006 | 78.005 | 77.139 | 74.369 | 68.541 | |
| MR_4 | 80.768 | 78.406 | 76.934 | 76.159 | 74.370 | 72.385 | 67.310 | |
| MR_5 | 80.419 | 79.087 | 76.985 | 75.837 | 73.425 | 71.527 | 68.649 | |
| MR_6 | 80.096 | 77.465 | 76.461 | 75.647 | 74.259 | 72.636 | 69.037 | |
| CT_1 | 73.825 | 71.617 | 70.066 | 69.070 | 68.514 | 66.688 | 64.308 | |
| CT_2 | 77.353 | 76.286 | 73.850 | 72.637 | 71.485 | 69.445 | 66.167 | |
| CT_3 | 78.335 | 76.462 | 71.751 | 70.298 | 69.245 | 67.099 | 64.723 | |
| Weighted average | 78.510 | 76.542 | 72.995 | 71.706 | 70.542 | 68.451 | 65.600 | |
Graphical representation of PSNR is shown in Fig. 9. PSNR values for 16-bit medical datasets are high as compared with 8-bit medical images. PSNR values are approximately same for 16-bit depth of standard and local hospital’s images at varying q levels. Weighted average of percentage difference in terms of PSNR values from q = 2 to q = 8 is 9.73%.
Fig. 9.
PSNR values obtained by proposed algorithm at varying q levels
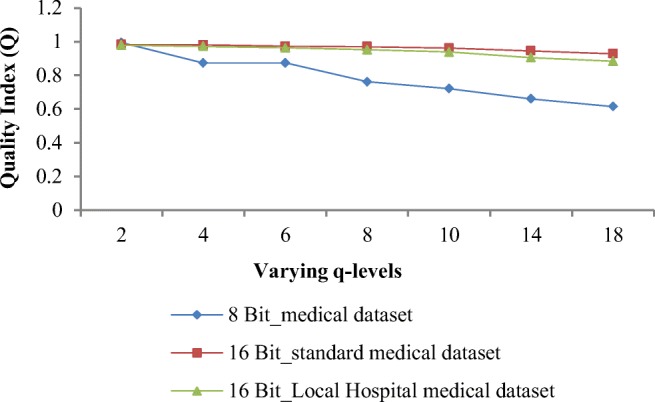
Figure 10 shows the graphical representation of quality index values that decreases with increase in q level. Weighted average of Q for all three datasets is 0.98 for q = 2 and for q = 8, it is 0.91. Q approaches to 1 indicate high quality of image. Quality index values at different q levels shown in Fig. 8 depict that high quality images are obtained for 16-bit medical datasets as compared with 8-bit medical datasets. Weighted average of Q values for 16-bit standard datasets and 16-bit local hospital’s image datasets at q = 8 are 0.961 and 0.939 respectively, whereas for 8-bit-depth medical dataset, weighted average of Q value is 0.762. Weighted average of percentage gap in terms of Q values from q = 2 to q = 8 is 7.48%. A tradeoff between PSNR, Q values, and BPP is to be maintained for accurate diagnosis for a near-lossless compression.
Fig. 10.
Q values obtained by proposed algorithm at varying q levels
The null hypothesis:
Ho: The quantization of image introduces an irreversible error, which in turn adversely affects the image quality and its diagnostic capability by the radiologist.
H1: The null hypothesis rejected.
After qualitative evaluation by the radiologists, it was established that the detection and estimation of pathology are possible up to q level of 8; i.e., there is no loss of diagnostically important information when the image is quantized at q level up to 8. Detection is still possible up to q level of 18, whereas estimation and detection both are achieved up to q level of 8. The optimal q level (q = 8) is provided in our research paper at which high compression efficiency is achieved without degrading the image quality. Quantization of image up to q level of 8 does not introduce any irreversible error which affects the image quality and its diagnostic capability. Quantitative analysis validates the finding of the radiologists.
Comparison of the Proposed Technique with State-of-the Art Techniques
The performance of the proposed near-lossless compression is compared with several state-of-the-art algorithms such as JPEG-LS, JPEG 2000 [36], CALIC [37] and SPIHT [38], and spatial prediction [2] for 8-bit dataset. Table 8 shows comparison of bit rate and PSNR results averaged across dataset obtained by our proposed method for the same dataset. As maximum tolerable distortion is q = 8, so in Table 8 results obtained by proposed technique at q = 2 and q = 8 is compared with existing techniques. In terms of BPP values, SPIHT have poor performance because zero-tree structure is used and is more appropriate for lossy compression. The proposed technique can compress medical images efficiently with little loss of information that is tolerable in medical diagnosis. When q = 2, i.e., minimum loss of information, performance of our proposed algorithm is comparable with other compression algorithms. When q = 8, performance of our algorithm in terms of BPP outperforms other existing JPEG-LS, JPEG 2000, CALIC, SPIHT, and spatial prediction algorithm by 38.29%, 44.70%, 41.22%, 63.86%, and 29.55% respectively. In terms of PSNR value, weighted average of PSNR for complete 8-bit medical dataset obtained by proposed technique is 60.96 dB when q level is 2. PSNR value of 60.96 dB is an excellent result for 8-bit-depth images. When q level is 8, weighted average of PSNR is approximately 51.35 dB obtained by proposed technique which is also a good result.
Table 8.
Comparison of BPP and PSNR for proposed technique and some other techniques
| Image Database | CALIC [37] | JPEG-LS [36] | JPEG-2000 [36] | SPIHT [38] | Spatial Prediction [2] | Proposed | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| q=2 | q=8 | q=2 | q=8 | |||||||||
| BPP | PSNR | BPP | PSNR | BPP | PSNR | BPP | PSNR | |||||
| CT_Apert | 1.178 | 0.984 | 1.271 | 2.365 | 1.269 | 61.04 | 1.054 | 48.68 | 1.188 | 65.237 | 0.653 | 50.487 |
| CT_corotid | 1.817 | 1.764 | 2.030 | 3.274 | 1.935 | 60.33 | 1.546 | 48.52 | 1.864 | 61.611 | 1.096 | 52.704 |
| CT_skull | 2.785 | 2.549 | 3.001 | 4.375 | 2.725 | 58.98 | 2.160 | 47.07 | 2.618 | 60.468 | 1.744 | 52.185 |
| CT_wrist | 1.780 | 1.515 | 1.767 | 3.148 | 1.855 | 60.27 | 1.458 | 48.53 | 1.813 | 60.712 | 1.107 | 52.234 |
| MRI_liver_T2 | 3.035 | 2.930 | 3.031 | 4.493 | 2.867 | 58.47 | 2.250 | 47.04 | 2.752 | 58.113 | 1.512 | 49.467 |
| MRI_Liver_T1 | 3.249 | 3.148 | 3.266 | 4.704 | 3.210 | 58.40 | 2.535 | 46.78 | 2.865 | 59.011 | 1.730 | 50.104 |
| MRI_chest | 2.413 | 2.410 | 2.582 | 3.731 | 2.494 | 60.07 | 1.999 | 48.37 | 2.165 | 61.075 | 1.663 | 50.255 |
| MRI_head | 2.598 | 2.573 | 2.915 | 4.336 | 2.814 | 58.73 | 2.314 | 46.62 | 2.700 | 61.203 | 1.642 | 50.259 |
| Mr_brain | 2.172 | 2.154 | 2.484 | 3.771 | 2.612 | 56.58 | 2.228 | 44.20 | 2.564 | 59.08 | 2.116 | 47.02 |
| Weighted average | 2.336 | 2.225 | 2.483 | 3.800 | 2.420 | 59.21 | 1.949 | 47.31 | 2.199 | 60.968 | 1.373 | 51.355 |
In the overall performance of proposed technique at optimal q level 8, weighted average value of BPP is 1.94 and PSNR is 51.35 dB for 8-bit-depth images.
The proposed algorithm and other existing near-lossless algorithms are compared with Table 9 in terms of BPP and PSNR values under q = 2 and q = 8. Results in Table 9 show BPP values of proposed algorithm which are lower than most of the algorithms. BPP values obtained by some other algorithms at q = 2 and q = 8 in Table 9 are lower than our proposed algorithm but at the cost of PSNR values. Our proposed algorithm outperforms other compared techniques in terms of quality parameter PSNR. Obtained PSNR value of proposed algorithm when q = 8 is even better than PSNR of other compared algorithms when q = 2. The quality of recovered image is preserved even for high q level, i.e., 8 and it is due to the inter-pixel redundancy removal by RIGED at optimal threshold and quantization is performed on RIGED predicted residual.
Table 9.
Comparison of PSNR and BPP for proposed technique and some other near-lossless compression techniques (results are averaged across all 8 bit medical data)
| q=2 | q=8 | |||
|---|---|---|---|---|
| PSNR (dB) | BPP | PSNR (dB) | BPP | |
| BP Coder [39] | 44.3 | 4.1 | 36.3 | 1.9 |
| SPIHT+AC [40] | 45.1 | 2.1 | 38.1 | 0.7 |
| DPCM [41] | 45.2 | 2.3 | 38.3 | 1.4 |
| JPEG-LS+WAT [42] | 45.1 | 3.5 | 38.5 | 2.3 |
| EC [43] | 49.2 | 1.0 | 38.8 | 0.3 |
| SPIHT [38] | 45.2 | 2.2 | 40.1 | 1.2 |
| Spatial Prediction [2] | 59.2 | 2.4 | 47.3 | 1.9 |
| Proposed Technique | 60.9 | 2.1 | 51.3 | 1.3 |
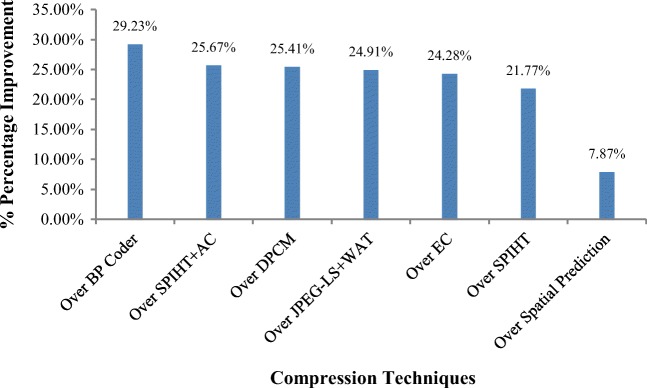
Percentage improvement of proposed technique in terms of PSNR over state-of-the-art near-lossless algorithms is obtained and depicted in Fig. 11. It is shown in figure below, the performance of proposed technique is 29.23%, 25.67%, 25.41%, 24.91%, 24.28%, 21.77%, and 7.87% better than BP Coder, SPIHT+AC, DPCM, JPEG-LS+WAT, EC, SPIHT, and spatial prediction algorithms respectively.
Fig. 11.
Percentage improvement of proposed technique in terms of PSNR over other near-lossless compression techniques
Performance of proposed technique for near-lossless compression is better achieved even with a high q level without any loss of information. Proposed algorithm with q = 8 achieves comparable bit rates with other near-lossless algorithms and high performance in terms of PSNR for benchmark datasets of different resolutions and medical dataset collected from local hospitals of different modalities.
Conclusion
Accounting for the characteristics of medical images, a near-lossless predictive coding algorithm is proposed for medical image sequences that preserve diagnostic information. The proposed technique employs RIGED predictor, quantizer, and block adaptive encoder. The RIGED provides optimal threshold value for effective prediction and the obtained residual image has lower entropy value. BAAE provides the optimal block size for encoding and optimal q level is provided for quantization in this paper at which high compression efficiency is achieved. Optimal q level for quantization is obtained by analyzing the recovered images qualitatively and quantitatively. After verification by the radiologist from the govt. hospital, it is concluded that the detection of an image is possible up to maximum q level of 18 and the estimation of an image is possible up to q level of 8. The q level of 8 is an optimal q level at which both estimation and detection can be achieved without losing the diagnostic capability from the image. The performance of the proposed technique in terms of PSNR for 16-bit standard datasets and 16-bit local hospital’s image datasets at q = 8 is 72.4 dB and 71.7 dB respectively, whereas for 8-bit-depth medical dataset, weighted average of PSNR is 51.3 dB. The proposed algorithm outperforms BP Coder, SPIHT+AC, DPCM, JPEG-LS+WAT, EC, SPIHT, and spatial prediction algorithms by 29.23%, 25.67%, 25.41%, 24.91%, 24.28%, 21.77%, and 7.87% respectively in terms of PSNR. Our empirical experimental results reveal that the proposed method is efficient for the near-lossless compression of medical images. Future work of this work will include design of near-lossless predictive coding for region of interest (ROI)-based image compression.
Electronic Supplementary Material
(PDF 3841 kb)
Acknowledgments
The authors would like to thank the Jaypee University Waknaghat, Distt. Solan, India, for supporting and providing help to this research. The authors would also like to thank the radiologists of Govt. Ripon Hospital, Distt. Shimla, for image quality assessment.
Footnotes
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Placidi G. Adaptive compression algorithm from projections: Application on medical greyscale images. Comput Biol Med. 2009;39(11):993–999. doi: 10.1016/j.compbiomed.2009.07.013. [DOI] [PubMed] [Google Scholar]
- 2.Song X, Huang Q, Chang S. Novel near-lossless compression algorithm for medical sequence images with adaptive block-based spatial prediction. J Digit Imaging. 2016;29(6):706–715. doi: 10.1007/s10278-016-9892-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Fidler A, Skaleric U, Likar B. The impact of image information on compressibility and degradation in medical image compression. Med Phys. 2006;33(8):2832–2838. doi: 10.1118/1.2218316. [DOI] [PubMed] [Google Scholar]
- 4.Chen K, Ramabadran T. Near-lossless compression of medical images through entropy-coded DPCM. IEEE Trans Med Imaging. 1994;13(3):538–548. doi: 10.1109/42.310885. [DOI] [PubMed] [Google Scholar]
- 5.Hartenstein H, Herz R, Saupe D: A comparative study of L1 distortionlimited image compression algorithms. Proc Picture Coding Symp:51–55, 1997
- 6.ISO/IEC JTC1/SC29/WG1 N505: Call for contributions for JPEG 2000 (JTC 1.29.14, 15444): Image Coding System. 1997
- 7.ISO/IEC JTC1/SC29/WG1 N390R. New work item: JPEG 2000 image coding system. 1997
- 8.ISO/IEC 15444-1, ITU-T Rec. T.800: Information technology – JPEG 2000 Image Coding System. Core Coding System. 2002
- 9.Jiang J, Grecos C. A low cost design of rate controlled JPEG-LS near lossless image compression. Image Vis Comput. 2001;19(3):153–164. doi: 10.1016/S0262-8856(00)00064-0. [DOI] [Google Scholar]
- 10.Caldelli R, Filippini F, Barni M. Joint near-lossless compressionand watermarking of still images for authentication and tamperlocalization. Signal Process-Image Commun. 2006;21(10):890–903. doi: 10.1016/j.image.2006.08.006. [DOI] [Google Scholar]
- 11.ISO/IEC 14495–1: Information Technology-Lossless and Nearlossless Compression of Continuous Tone Still Images. Baseline. Dec. 1999. JPEG-LS source code available at: http://www.stat. columbia.edu/%7Ejakulin/jpeg-ls/mirror.htm, 1999
- 12.Ayinde B: A Fast and Efficient Near-Lossless Image Compression using Zipper Transformation. arXiv preprint arXiv:1710.02907, 2017
- 13.Khobragade PB, Thakare SS. Design and analysis of near lossless image compression technique. Progress Sci Eng Res J. 2014;2(3):193–200. [Google Scholar]
- 14.Beerten J, Blanes I, Serra-Sagristà J. A fully embedded two-stage coder for hyperspectral near-lossless compression. IEEE Geosci Remote Sens Lett. 2015;12(8):1775–1779. doi: 10.1109/LGRS.2015.2425548. [DOI] [Google Scholar]
- 15.Boopathiraja S, Kalavathi P. A near lossless multispectral image compression using 3D-DWT with application to LANDSAT images. Int J Comput Sci Eng. 2018;6(4):332–336. [Google Scholar]
- 16.Zhang X, Wu X: Near-lossless l∞ constrained multi-rate image decompression via deep neural network. IEEE Trans Image Process, 2018 arXiv:1801.07987v3 [cs.CV], 2018
- 17.Simić N, Perić ZH, Savić MS. Image coding algorithm based on Hadamard transform and simple vector quantization. Multimed Tools Appl. 2018;77(5):6033–6049. doi: 10.1007/s11042-017-4513-4. [DOI] [Google Scholar]
- 18.Bartrina-Rapesta J, Marcellin MW, Serra-Sagristà J, Hernández-Cabronero M: A Novel Rate-Control for Predictive Image Coding with Constant Quality. IEEE Access, 2019
- 19.Valsesia D, Magli E. Fast and lightweight rate control for onboard predictive coding of hyperspectral images. IEEE Geosci Remote Sens Lett. 2017;14(3):394–398. doi: 10.1109/LGRS.2016.2644726. [DOI] [Google Scholar]
- 20.Sharma U, Sood M, Puthooran E: A novel resolution independent gradient edge predictor for lossless compression of medical image sequences. Int J Comput Appl, 2019. 10.1080/1206212X.2019.1610994
- 21.Sharma U, Sood M, Puthooran E. Implementation and Performance Assessment of Gradient Edge Detection Predictor for Reversible Compression of Biomedical Image. Commun Comput Inform Sci (CCIS) 2018;955:1–11. doi: 10.1007/978-981-13-3140-4_18. [DOI] [Google Scholar]
- 22.Sharma U, Sood M, Puthooran E: A Block-based arithmetic entropy encoding scheme for medical images: block-based arithmetic entropy encoding scheme. International Journal of Healthcare Information Systems and Informatics (IJHISI) 15 (3) (in press)
- 23.Avramovic A. On predictive-based lossless compression of images with higher bit depths. Telfor J. 2012;4(2):122–127. [Google Scholar]
- 24.Weinberger M, Seroussi G, Sapiro G. The LOCO-I lossless image compression algorithm: Principles and standardization into JPEGLS. IEEE Trans Image Process. 2000;9(8):1309–1324. doi: 10.1109/83.855427. [DOI] [PubMed] [Google Scholar]
- 25.Shridevi S, Vijaykumar V. Anuja: a survey on various compression methods for medical images. Int J Intell Syst Appl. 2012;4(3):13–19. [Google Scholar]
- 26.Ayoobkhan M, Chikkannan E, Ramakrishnan K: Lossy image compression based on prediction error and vector quantization. EURASIP J Image Video Process 7 (1), 2017
- 27.Prabhash C: Medical image compression by using IWT & linear predictive coding. GADL J Inven Comput Sci Commun Technol (JICSCT) 2 (2), 2016
- 28.Cavaro-Ménard C, Zhang L, Callet P: Diagnostic quality assessment of medical images: Challenges and trends. Eur Workshop Visual Inform Process (EUVIP), 277–284, 2010
- 29.“CIPR.”[Online]. Available: http://www.cipr.rpi.edu/resource/sequences/sequence01.html
- 30.Clark K, Vendt B, Smith K. The Cancer Imaging Archive (TCIA): maintaining and operating a public information repository. J Digit Imaging. 2013;26(6):1045–1057. doi: 10.1007/s10278-013-9622-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Grove et al: Data from Quantitative computed tomographic descriptors associate tumor shape complexity and intratumor heterogeneity with prognosis in lung adenocarcinoma. The Cancer Imaging Archive, 2015 [Online]. Available: doi:10.7937/K9/TCIA.2015.A6V7JIWX [DOI] [PMC free article] [PubMed]
- 32.Barboriak D: Data from RIDER_NEURO_MRI. The Cancer Imaging Archive, 2015
- 33.Meyer et al: Data from RIDER Breast MRI. The Cancer Imaging Archive, 2015. [Online]. Available: doi:10.7937/K9/TCIA.2015.H1SXNUXL
- 34.Puthooran E, Anand R, Mukherjee S. Lossless compression of medical images using a dual level DPCM with context adaptive switching neural network predictor. Int J Comput Intel Syst. 2013;6:1082–1093. doi: 10.1080/18756891.2013.816059. [DOI] [Google Scholar]
- 35.Bhardwaj C, Urvashi SM. Implementation and performance assessment of compressed sensing for images and video signals. J Global Pharma Technol. 2017;6:123–133. [Google Scholar]
- 36.ISO/IEC JTC 1/SC 29/WG 1, ISO/IEC FCD 15444–1: Information Technology – JPEG 2000 Image Coding System. JPEG2000. 2000 source code available at: http://www.kakadusoftware.com/
- 37.Wu X, Memon N: CALIC—A context based adaptive lossless image codec. Proc ICASSP 4, 1890–1893, 1996. CALIC source code available at: http://compression.graphicon.ru/download/sources/i_glless/codec.zip
- 38.Said A, Pearlman W. A new, fast, and efficient image codec based on set partitioning in hierarchical trees. IEEE Trans Circuits Syst Video Technol. 1996;6(3):243–250. doi: 10.1109/76.499834. [DOI] [Google Scholar]
- 39.Miguel A, Riskin E, Ladner R. Near-lossless and lossy compression of imaging spectrometer data: comparison of information extraction performance. SIViP. 2012;6(4):597–611. doi: 10.1007/s11760-010-0191-7. [DOI] [Google Scholar]
- 40.Yea S, Pearlman W. A wavelet-based two-stage near-lossless coder. IEEE Trans Image Process. 2006;15(11):3488–3500. doi: 10.1109/TIP.2006.877525. [DOI] [PubMed] [Google Scholar]
- 41.Hartenstein H, Herz R, Saupe D: A comparative study of L1 distortion limited image compression algorithms. Proc Picture Coding Symp. 51–55, 1997.
- 42.Caldelli R, Filippini F, Barni M. Joint near-lossless compression and watermarking of still images for authentication and tamper localization. Signal Process-Image Commun. 2006;21(10):890–903. doi: 10.1016/j.image.2006.08.006. [DOI] [Google Scholar]
- 43.Aràndiga F, Mulet P, Renau V. Lossless and near-lossless image compression based on multiresolution analysis. J Comput Appl Math. 2013;242:70–81. doi: 10.1016/j.cam.2012.10.028. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(PDF 3841 kb)