Abstract
In this paper, we analyze the network properties of the Italian e-MID data based on overnight loans during the period 1999–2010. We show that the networks appear to be random at the daily level, but contain significant non-random structure for longer aggregation periods. In this sense, the daily networks cannot be considered as being representative for the underlying ‘latent’ network. Rather, the development of various network statistics under time aggregation points toward strong non-random determinants of link formation. We also identify the global financial crisis as a significant structural break for many network measures.










Similar content being viewed by others
Notes
In the literature, the traditional approach is to focus on the optimal liquidity management of a particular financial institution, see e.g. Brodt (1978) and Ho and Saunders (1985). Recently, Brunnermeier and Pedersen (2009) introduced the distinction between funding liquidity and market liquidity in a theoretical model, showing that their relationship may give rise to systemic crises.
In the following, matrices will be written in bold, capital letters. Vectors and scalars will be written as lower-case letters.
This is true when we think of individual banks as consolidated entities.
Directed means that \(d_{i,j}\ne d_{j,i}\) in general. Sparse means that at any point in time the number of links is only a small fraction of the \(N(N-1)\) possible links. Valued means that interbank claims are reported in monetary values as opposed to 1 or 0 in the presence or absence of a claim, respectively.
The vast majority of trades (roughly 95 %) is conducted in Euro.
This development is driven by the fact that the market is unsecured. The recent financial crisis made unsecured loans in general less attractive, with stronger impact for longer maturities. It should be noted, that there is also a market for secured loans called e-MIDER.
The minimum quote size could pose an upward bias for participating banks. It would be interesting to check who are the quoting banks and who are the aggressors. Furthermore it would be interesting to look at quote data, as we only have access to actual trades.
More details can be found on the e-MID website, see http://www.e-mid.it/.
Similar developments are reported by Bech and Atalay (2010) for the federal funds market.
The Figure was produced using visone, http://www.visone.info/, by Brandes and Wagner (2004).
For a detailed analysis of the trading strategies in the e-MID, see Fricke (2012).
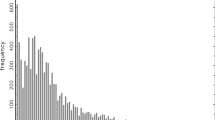
In a companion paper, we focus explicitly on fitting the degree distribution, see Fricke and Lux (2013). The main findings are: (1) the degree distributions are unlikely to follow power-laws, and (2) the in- and out-degrees do not follow the same distribution.
Note that mostly because of the shrinking number of active banks all statistics decrease over time, irrespective of the aggregation period.
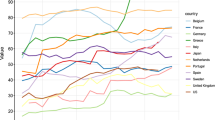
The density for the total network, including the foreign banks, seems to steadily decline over the sample period. This illustrates the fact that the increasing fraction of foreign banks are less interconnected with the (smaller) Italian banks.
Additionally, the electronic nature of the trading platform simplifies the trading between any two counterparties, i.e. increases the probability of observing any link.
The power-law distribution with tail exponent 2.3 is a common finding in many interbank markets, see e.g. Boss et al. (2004). The resulting sequences of the out-degrees, i.e. the simulated quasi-daily networks, are attributed to the nodes by ranking those according to the observed out-degrees, considering only active banks during the particular day. Note that if we did not account for the ordering of the observed degree sequences, we would end up with very similar aggregation properties as in the Erdös-Renyi case. The in-degrees are distributed in a random uniform way, ruling out self-links and counting each link at most once.
Note that the density of aggregated Erdös-Renyi networks can be written as
$$\begin{aligned} \rho _{T}^{r}= 1 - \prod _{t=1}^{T} (1-\rho _{t}^{r}), \end{aligned}$$where \((1-\rho _{t}^{r})\) is the probability of observing no links in the network at time \(t\). Since we adjust the number of active banks on a daily basis these probabilities would not exactly coincide with the results of our simulations.
The literature on interbank networks is surprisingly silent about the choice of the aggregation period. We are aware of only one paper, namely Kyriakopoulos et al. 2009, investigating this issue.
The so-called graph correlation, see e.g. Butts and Carley (2001), shows qualitatively very similar results, but is not able to cope with banks entering or exiting the market. The correlation of both measures is always above \(.9\) irrespective of the aggregation period.
See Snijders et al. (2009).
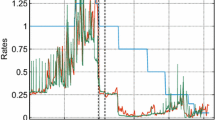
We should note that, as apparent from Fig. 6, the reason for the 10th percentile to be below the 0.2 threshold is not the GFC.
A structural break (after the GFC) is detected by a Chow-test as well as an additional CUSUM test for the 10th year, the 39th quarter and the 117th month respectively, but not for daily networks. For the yearly networks only the Chow-test indicates a structural break. Note that the yearly analysis involves only 12 data points.
Again the results are qualitatively very similar for the other years as well.
This problem occurs for each aggregation period, but is likely to become more pronounced for longer frequencies.
For more detailed definitions of clustering coefficients see Zhou (2002).
Any connection along directed links between two nodes i and j is called a path and the length of the path is defined as the number of edges crossed. There are no restrictions on visiting a node or link more than once alongside a path.
The probability of random link is exactly the density of 0.208.
Small ASPLs have been detected for social, information, technological and biological networks. The first empirical finding dates back to the chain letter experiments conducted by Milgram (1967). His finding that on average only six acquaintances are needed to form a link between two random selected persons led to the famous phrase of ‘six degrees of separation’.
It is not necessary for two nodes to have a shortest path, since there might be no link leading from one to the other. In this case the two nodes lie in different components of the network and by convention the length of these non-existing geodesic paths are set to infinity. The undirected banking network consists always of only one connected component and the same is true for the simulated random networks, because of the high density.
The results are qualitatively the same for the directed version of the network. The ASPL for the quarterly networks is 1.912, while we obtain 1.776 for the scale-free and 1.802 for the Erdös-Renyi networks. The \(CC^{2}\) (0.571) is significantly higher than for the scale free with 0.342 and Erdös-Renyi networks with 0.208, whereas \(CC^{1}\) (0.164) is smaller. However, in this case the network consists not only of one giant component, but might contain separate clusters, which makes the interpretation of the ASPL more difficult.
See also Fricke and Lux (2012).
See Brunnermeier (2008).
The correlation between both is 0.963 for this period and 0.957 over the complete sample.
Fricke and Lux (2012) show that most of these changes were in fact driven by behavioral changes of core banks.
As noted above, this is not true for loans longer than overnight. These markets essentially collapsed completely, which is not surprising given that the loans are unsecured.
This means that banks do not consider the complete network, e.g. indirect relations, during the network formation process, although they could, in principle, infer such information from the e-MID platform.
With respect to the stability of relationships, the working of the interbank market seems not too different from that of the often-studied fish market. Here as well, stable links might underscore the importance of trust between buyer and seller as well as the element of complexity reduction in a day-to-day task where excessive shopping for good prices seems much less important than trust in the reliability of the counterpart, cf. Kirman and Vriend (2001), Gallegati et al. (2011).
Fricke and Lux (2012) show that mostly core banks reduced their lending activity but at the same time increased their borrowing from their counterparties in the periphery.
No bank from outside Europe traded in the Euro segment of the e-MID interbank market in the whole sample period.
References
Allen F, Gale D (2000) Financial contagion. J Political Econ 108(1):1–33
Basle Committee on Banking Supervision (2008) Principles for sound liquidity risk management and supervision. Framework publication, Bank of International Settlements, Basel
Beaupain R, Durré A (2012) Nonlinear liquidity adjustments in the Euro area overnight money market, Working Paper Series 1500, European Central Bank, Germany
Bech M, Atalay E (2010) The topology of the Federal funds market. Phy A 389(22):5223–5246
Boss M, Elsinger H, Summer M, Thurner S (2004) Network topology of the interbank market. Quant Finance 4(6):677–684
Brandes U, Wagner D (2004) Visone-analysis and visualization of social networks. In: Jünger M, Mutzel P (eds) Graph Drawing Software. Springer-Verlag, Berlin, pp 321–340
Brodt AI (1978) A dynamic balance sheet management model for a Canadian chartered bank. J Bank Finance 2(3):221–241
Brunnermeier MK (2008) Deciphering the liquidity and credit crunch 2007–08, Working Paper 14612, National Bureau of Economic Research, Cambridge
Brunnermeier MK, Pedersen LH (2009) Market liquidity and funding liquidity. Rev Financial Stud 22(6):2201–2238
Butts C, Carley K (2001) Multivariate methods for interstructural analysis. CASOS Working Paper. Carnegie Mellon University, Pittsburgh
Cocco JF, Gomes FJ, Martins NC (2009) Lending relationships in the Interbank market. J Financial Intermed 18(1):24–48
Craig B, von Peter G (2010) Interbank Tiering and Money Center Banks, Discussion Paper, Series 2: Banking and Financial Studies 12/2010, Deutsche Bundesbank
De Masi G, Iori G, Caldarelli G (2006) Fitness model for the Italian interbank money market. Phys Rev E 74(6):66112
Elsinger H, Lehar A, Summer M (2006) Using market information for banking system risk assessment. Intern J Cent Bank 2(1):1–29
Finger K, Lux T (2013) The evolution of the Banking network: an actor-oriented approach, unpublished manuscript
Fricke D (2012) Trading strategies in the overnight money market: correlations and clustering on the e-MID trading platform. Phy A 391:6528–6542
Fricke D, Lux T (2012) Core-periphery structure in the overnight money market: evidence from the e-MID trading platform, Kiel Working Paper 1759, Kiel Institute for the World Economy, Germany
Fricke D, Lux T (2013) On the distribution of links in the Interbank network: evidence from the e-MID overnight money market, Kiel Working Paper 1819, Kiel Institute for the World Economy, Germany
Gallegati M, Giulioni G, Kirman A, Palestrini A (2011) What’s that got to do with the price of fish? Buyers behavior on the Ancona fish market. J Econ Behav Organ 80(1):20–33
Ho TSY, Saunders A (1985) A micro model of the Federal funds market. J Finance 40(3):977–988
IIF Special Committee on Liquidity Risk (2007) Principles of liquidity risk management. Framework publication, Institute of International Finance, Finance
Inaoka H, Ninomyia T, Taniguchi K, Shimizu T, Takayasu H (2004) Fractal network derived from banking transaction: an analysis of network structures formed by financial institutions. Bank of Japan Working Papers
Iori G, De Masi G, Precup OV, Gabbi G, Caldarelli G (2008) A network analysis of the Italian overnight money market. J Econ Dyn Cont 32(1):259–278
Kirman AP, Vriend NJ (2001) Evolving market structure: an ACE model of price dispersion and loyalty. J Econ Dyn Cont 25(3–4):459–502
Kyriakopoulos F, Thurner S, Puhr C, Schmitz SW (2009) Network and eigenvalue analysis of financial transaction networks. Europ Phy J B 71(4):523–531
Milgram S (1967) The small-world problem. Psychol Today 2:60–67
Montagna M, Lux T (2013) Hubs and resilience: towards more realistic models of the Interbank markets, Kiel Working Paper 1826, Kiel Institute for the World Economy, Germany
Préfontaine J, Desrochers J, Godbout L (2010) The analysis of comments received by the BIS on “Principles for sound liquidity risk management and supervision”. Intern Bus Econ Res J 9(7):65–72
Snijders TAB, van de Bunt GG, Steglich CEG (2009) Introduction to stochastic actor-based models for network dynamics. Soc Netw 32(1):44–60
Soramaki K, Bech ML, Arnold J, Glass RJ, Beyeler W (2007) The topology of interbank payment flows. Phy A 379:317–333
Watts DJ, Strogatz SH (1998) Collective dynamics of small-world networks. Nature 393(6684):440–442
Wilkinson I, Young L (2002) On cooperating: firms, relations and networks. J Bus Res 55(2):123–132
Zhou H (2002) Scaling exponents and clustering coefficients of a growing random network. Phys Rev E 66:016125
Author information
Authors and Affiliations
Corresponding author
Additional information
The article is part of a research initiative launched by the Leibniz Community. We are grateful to Christian Freund and Mattia Montagna for intense discussion on the analysis of interbank networks, and to two anonymous referees for their helpful comments and suggestions.
Rights and permissions
About this article
Cite this article
Finger, K., Fricke, D. & Lux, T. Network analysis of the e-MID overnight money market: the informational value of different aggregation levels for intrinsic dynamic processes. Comput Manag Sci 10, 187–211 (2013). https://doi.org/10.1007/s10287-013-0171-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10287-013-0171-9