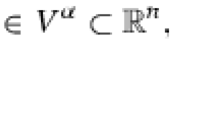Abstract
Robust optimization is an important technique to immunize optimization problems against data uncertainty. In the case of a linear program and an ellipsoidal uncertainty set, the robust counterpart turns into a second-order cone program. In this work, we investigate the efficiency of linearizing the second-order cone constraints of the latter. This is done using the optimal linear outer-approximation approach by Ben-Tal and Nemirovski (Math Oper Res 26:193–205, 2001) from which we derive an optimal inner approximation of the second-order cone. We examine the performance of this approach on various benchmark sets including portfolio optimization instances as well as (robustified versions of) the MIPLIB and the SNDlib.
















Similar content being viewed by others
References
Ben-Tal A, Nemirovski A (2000) Robust solutions of linear programming problems contaminated with uncertain data. Math Program A 88:411–424
Ben-Tal A, Nemirovski A (2001) On polyhedral approximations of the second-order cone. Math Oper Res 26:193–205
Ben-Tal A, El Ghaoui L, Nemirovski A (2009) Robust optimization. Princeton University Press
Bertsimas D, Sim M (2003) Robust discrete optimization and network flows. Math Program B 98:49–71
Bertsimas D, Sim M (2004) The price of robustness. Oper Res 52(1):35–53
Bertsimas D, Sim M (2006) Tractable approximations to robust conic optimization problems. Math Program B 107:5–36
Bertsimas D, Pachamanovab D, Sim M (2004) Robust linear optimization under general norms. Oper Res Lett 32:510–516
Bertsimas D, Brown D, Caramanis C (2011) Theory and applications of robust optimization. SIAM Rev 53(3):464–501
Bonnans JF, Gilbert JC, Lemaréchal C, Sagastizábal CA (2009) Numerical optimization—theoretical and practical aspects. Springer, New York
Boost C++ Libraries (2013) Boost random number library. http://www.boost.org/doc/libs/1_38_0/libs/random
Conforti M, Cornuéjols G, Zambelli G (2010) Extended formulations in combinatorial optimization. 4OR 8(1):1–48
Dolan E, Moré J (2002) Benchmarking optimization software with performance profiles. Math Program A 91(2):201–213
Fiorini S, Rothvoß T, Tiwary H (2012) Extended formulations for polygons. Discret Comput Geom 48(3):658–668
Gay M (1985) Electronic mail distribution of linear programming test problems. Math Program Soc COAL Bull 13:10–12. http://www.netlib.org/netlib/lp
Glineur F (2000) Computational experiments with a linear approximation of second-order cone optimization. Image Technical Report 001, Faculté Polytechnique de Mons
Glineur F (2001) Conic optimization: an elegenat framework for convex optimization. Belg J Oper Res Stat Comput Sci 41(1–2):5–28
Gurobi Optimization, Inc (2013) Gurobi optimizer reference manual. http://www.gurobi.com
Kaibel V (2011) Extended formulations in combinatorial optimization. Optima 85:2–7
Kaibel V, Pashkovich K (2011) Constructing extended formulations from reflection relations. Proc IPCO 2011:287–300
Koch T, Achterberg T, Andersen E, Bastert O, Berthold T, Bixby R, Danna E, Gamrath G, Gleixner A, Heinz S, Lodi A, Mittelmann H, Ralphs T, Salvagnin D, Steffy D, Wolter K (2011) MIPLIB 2010. Math Program Comput 3(2):103–163
Orlowski S, Pióro M, Tomaszewski A, Wessäly R (2007) SNDlib 1.0–survivable network design library. In: Proceedings of the 3rd International Network Optimization Conference (INOC 2007), Spa, Belgium
Vielma J, Ahmed S, Nemhauser GL (2008) A lifted linear programming branch-and-bound algorithm for mixed integer conic quadratic programs. INFORMS J Comput 20(3):438–450
Author information
Authors and Affiliations
Corresponding author
Additional information
Research reported in this paper was partially supported by NSF Grant CMMI-1300144, BMBF Grant 05M10WEC, WTT Grant 12190-1, DLR Grant 10-220210-C4 and ComplexWorld Research Network Grant.
An erratum to this article is available at http://dx.doi.org/10.1007/s10287-016-0269-y.
Rights and permissions
About this article
Cite this article
Bärmann, A., Heidt, A., Martin, A. et al. Polyhedral approximation of ellipsoidal uncertainty sets via extended formulations: a computational case study. Comput Manag Sci 13, 151–193 (2016). https://doi.org/10.1007/s10287-015-0243-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10287-015-0243-0
Keywords
- Robust optimization
- Approximation
- Extended formulations
- Second-order cone optimization
- Mixed-integer programming
- Portfolio optimization