Robust selective maintenance optimization of series–parallel mission-critical systems subject to maintenance quality uncertainty

Abstract

This paper studies the optimization of the joint selective maintenance and repairperson assignment problem when the quality of maintenance actions is uncertain, thus leading to uncertain post-maintenance reliability of system components. This situation is common in practice since maintenance actions are never perfect and are affected by several factors such as the qualification and the degree of expertise of the repairpersons, the maintenance methods and tools used, and naturally occurring operating environment variability. Using a robust optimization framework, the maintenance quality uncertainty is captured via non-symmetric budget uncertainty sets that enable the level of decision-maker conservatism to be controlled. Both the nominal (i.e., deterministic) and robust problems are reformulated as mixed-integer exponential conic programs that can be solved using currently available solvers. Extensive numerical experiments on benchmark instances show the favorable computational performance of the proposed reformulations and the value of considering maintenance quality uncertainty when developing selective maintenance plans.

Appendix 1: Two-phase approach

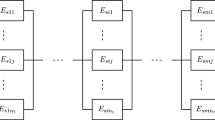
Diallo et al. (2019) devised a decomposition method to represent the JSM-RAP as a binary integer program (BIP). In the first phase, a methodical and structured approach generates an exhaustive set of patterns containing all potential combinations of components, repairpersons, and maintenance levels. The second phase focuses on solving a BIP (demonstrated below) that optimizes the choice of a sequence of patterns, aiming to maximize system reliability.

$$\begin{aligned}{}[\mathcal {SMP}]_{BIP}:\quad&\max _{x_{ip}} \ln {({\mathcal {R}})}=\;{} & {} \sum ^{I}_{i=1}{\sum ^{P_i}_{p=1}\ln {({R_{ip})}. x_{ip}}} \end{aligned}$$

(28a)

$$\begin{aligned}&\quad \text {s.t.:}\nonumber \\{} & {} {}&\sum ^{P_i}_{p=1}x_{ip} = 1 \quad{} & {} \forall i \end{aligned}$$

(28b)

$$\begin{aligned}{} & {} {}&\sum ^{I}_{i=1}{\sum ^{P_i}_{p=1}{C_{ip} . x_{ip}}} \le C_{0} \quad{} & {} \end{aligned}$$

(28c)

$$\begin{aligned}{} & {} {}&\sum ^{I}_{i=1}{\sum ^{P_i}_{p=1}{T_{ipr} . x_{ip}}} \le D_{0} \quad{} & {} \forall r \end{aligned}$$

(28d)

$$\begin{aligned}{} & {} {}&x_{ip}\in \{0,1\} \quad{} & {} \forall i, \forall p, \end{aligned}$$

(28e)

where $i \in \left\{ 1, \dots , I\right\}$ is the index of the subsystems, $p \in \left\{ 1, \dots ,\ P_{i}\right\}$ is the index of patterns generated for subsystem i, $C_{0}$ is the maintenance budget available, $D_{0}$ is the break duration, $T_{ipr}$ is the time spent by repair person r on subsystem i under pattern p, and $C_{ip}$ is the maintenance cost of pattern p for subsystem i. The binary decision variables $x_{ip}$ represents the selection or not of pattern p for subsystem i.

Constraint (28b) guarantees that precisely one maintenance pattern is chosen for each subsystem. Ensuring that the total maintenance cost does not exceed the available maintenance budget is achieved through constraint (28c). Constraint (28d) stipulates that a repair person must be hired before they can perform work, and they cannot work beyond the break duration. The final constraint (28e), define the binary decision variable $x_{ip}$ utilized in the formulation.