Abstract
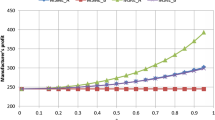
This paper addresses the channel coordination problem in a green supply chain consisting of a manufacturer and a retailer, in which the manufacturer controls green innovation and wholes price, while the retailer controls sales price. Pricing and green innovation strategies in integrated and decentralized channels are computed and compared, and a two-part tariff contract is designed to coordinate the decentralized supply chain. A Nash bargaining model is further developed to distribute the extra-profit between channel members. A numerical example is conducted to explore the impacts of green effectiveness and operational inefficiency effect on optimal/equilibrium solutions and coordination. The main results show that the green innovation investment, energy efficiency level and channel profit of integrated channel are larger than those of decentralized one, but the relationship of sales prices under two channel structures depends on system parameters. Green effectiveness exerts a positive effect on optimal/equilibrium solutions. The coordinator’s coordination capability is improved by green effectiveness, but weakened by operational inefficiency effect.








Similar content being viewed by others
References
Aguilera-Caracuel J, Ortiz-de-Mandojana N (2013) Green innovation and financial performance an institutional approach. Organ Environ 26(4):365–385
Banerjee A, Solomon B (2003) Eco-labeling for energy efficiency and sustainability: a meta-evaluation of US programs. Energy Policy 31(2):109–123
Barari S, Agarwal G, Zhang W et al (2012) A decision framework for the analysis of green supply chain contracts: an evolutionary game approach. Expert Systems with Applications 39(3):2965–2976
Bemporad R, Baranowski M (2007) Conscious consumers are changing the rules of marketing. Are You Ready? Highlights from the BBMG Conscious Consumer Report
Bhaskaran S, Krishnan V (2009) Effort, revenue, and cost sharing mechanisms for collaborative new product development. Manag Sci 55(7):1152–1169
BP (2011) BP Statistical review of world energy 2011
Cachon G (2003) Supply chain coordination with contracts. Handb Oper Res Manag Sci 11:227–339
Cachon G, Lariviere M (2005) Supply chain coordination with revenue-sharing contracts: strengths and limitations. Manag Sci 51(1):30–44
Chitra K (2007) In search of the green consumers: a perceptual study. J Serv Res 7(1):173–191
Choi T, Li Y, Xu L (2013) Channel leadership, performance and coordination in closed loop supply chains. Int J Prod Econ 146(1):371–380
Cronin J Jr, Smith J, Gleim M et al (2011) Green marketing strategies: an examination of stakeholders and the opportunities they present. J Acad Mark Sci 39(1):158–174
Cuerva M, Triguero-Cano A, Corcoles D (2014) Drivers of green and non-green innovation: empirical evidence in Low-Tech SMEs. J Clean Prod 68:104–113
De Giovanni P (2011) Quality improvement vs. advertising support: which strategy works better for a manufacturer? Euro J Oper Res 208(2):119–130
De Giovanni P, Zaccour G (2014) A two-period game of a closed-loop supply chain. Euro J Oper Res 232(1):22–40
Dixon R, McGowan E, Onysko G et al (2010) US energy conservation and efficiency policies: challenges and opportunities. Energy Policy 38(11):6398–6408
Drake D, Kleindorfer P, Van Wassenhove L (2012) Technology choice and capacity portfolios under emissions regulation (working paper)
EI Saadany A, Jaber M (2010) A production/remanufacturing inventory model with price and quality dependant return rate. Comput Ind Eng 58(3):352–362
Frondel M, Horbach J, Renning K (2008) What triggers environmental management and innovation? Empir Evid Ger Ecol Econ 66(1):153–160
Gaspar R, Antunes D (2011) Energy efficiency and appliance purchases in Europe: consumer profiles and choice determinants. Energy Policy 39(11):7335–7346
Ghosh D, Shah J (2012) A comparative analysis of greening policies across supply chain structures. Int J Prod Econ 135(2):568–583
Ghosh D, Shah J (2015) Supply chain analysis under green sensitive consumer demand and cost sharing contract. Int J Prod Econ 164:319–329
He X, Krishnamoorthy A, Prasad A et al (2012) Co-op advertising in dynamic retail oligopolies. Decis Sci 43(1):73–106
Jeuland A, Shugan S (1983) Managing channel profits. Mark Sci 2(3):239–272
Karakayali I, Emir-Farinas H, Akcali E (2007) An analysis of decentralized collection and processing of end-of-life products. J Oper Manag 25(6):1161–1183
Karray S (2015) Cooperative promotions in the distribution channel. Omega 51:49–58
Khanna N, Zhou N, Fridley D et al (2013) Evaluation of China’s local enforcement of energy efficiency standards and labeling programs for appliances and equipment. Energy Policy 63:646–655
Krass D, Nedorezov T, Ovchinnikov A (2013) Environmental taxes and the choice of green technology. Prod Oper Manag 22(5):1035–1055
Lambertini L (2014) Coordinating static and dynamic supply chains with advertising through two-part tariffs. Automatica 50(2):565–569
Li B, Zhu M, Jiang Y et al (2016) Pricing policies of a competitive dual-channel green supply chain. J Clean Prod 112:2029–2042
Lin H, Zeng S, Ma H et al (2014) Can political capital drive corporate green innovation? Lessons from China. J Clean Prod 64:63–72
Lin R, Tan K, Geng Y (2013) Market demand, green product innovation, and firm performance: evidence from Vietnam motorcycle industry. J Clean Prod 40:101–107
Liu Z, Anderson T, Cruz J (2012) Consumer environmental awareness and competition in two-stage supply chains. Euro J Oper Res 218(3):602–613
López M, Garcia A, Rodriguez L (2007) Sustainable development and corporate performance: a study based on the Dow Jones sustainability index. J Bus Eth 75(3):285–300
Martín-Herrán G, Taboubi S (2015) Price coordination in distribution channels: a dynamic perspective. Euro J Oper Res 240(2):401–414
Moorthy S (1987) Managing channel profits: comments. Mark Sci 6(4):375–379
Muthulingam S, Corbett C, Benartzi S et al (2013) Energy efficiency in small and medium-sized manufacturing firms: order effects and the adoption of process improvement recommendations. Manuf Serv Opera Manag 15(4):596–615
Nash J Jr (1950) The bargaining problem. Econom J Econom Soc 18(2):155–162
Patterson M (1996) What is energy efficiency? Concepts, indicators and methodological issues. Energy policy 24(5):377–390
Rennings K (2000) Redefining innovation-eco-innovation research and the contribution from ecological economics. Ecolo Econ 32(2):319–332
Sarkis J (2003) A strategic decision framework for green supply chain management. J Clean Prod 11(4):397–409
Sayadi M, Makui A (2014) Feedback nash equilibrium for dynamic brand and channel advertising in dual channel supply chain. J Optim Theory Appl 161(3):1012–1021
Schiederig T, Tietze F, Herstatt C (2012) Green innovation in technology and innovation management-an exploratory literature review. R&D Manag 42(2):180–192
Shi X (2014) Setting effective mandatory energy efficiency standards and labelling regulations: a review of best practices in the Asia Pacific region. Appl Energy 133:135–143
Swami S, Shah J (2012) Channel coordination in green supply chain management. J Oper Res Soc 64(3):336–351
Testa F, Iraldo F (2010) Shadows and lights of GSCM (green supply chain management): determinants and effects of these practices based on a multinational study. J Clean Prod 18(10):953–962
Vachon S, Klassen R (2006) Extending green practices across the supply chain: the impact of upstream and downstream integration. Int J Oper Prod Manag 26(7):795–821
Vörös J (2006) The dynamics of price, quality and productivity improvement decisions. Euro J Oper Res 170(3):809–823
Xie J, Neyret A (2009) Co-op advertising and pricing models in manufacturer-retailer supply chains. Computers & Industrial Engineering 56(4):1375–1385
Xie J, Wei J (2009) Coordinating advertising and pricing in a manufacturer-retailer channel. Euro J Oper Res 197(2):785–791
Xie G, Yue W, Liu W et al (2012) Risk based selection of cleaner products in a green supply chain. Pac J Optim 8(3):473–484
Xie G (2015) Modeling decision processes of a green supply chain with regulation on energy saving level. Comput Oper Res 54:266–273
Yao X, Liu Y, Yan X (2014) A quantile approach to assess the effectiveness of the subsidy policy for energy-efficient home appliances: evidence from Rizhao, China. Energy Policy 73:512–518
Young W, Hwang K, McDonalds S et al (2010) Sustainable consumption: green consumer behavior when purchasing products. Sustain Dev 18(1):20–31
Zaccour G (2008) On the coordination of dynamic marketing channels and two-part tariffs. Automatica 44(5):1233–1239
Zhang C, Liu L (2013) Research on coordination mechanism in three-level green supply chain under non-cooperative game. Appl Math Model 37(5):3369–3379
Zhang L, Wang J, You J (2015) Consumer environmental awareness and channel coordination with two substitutable products. Euro J Oper Res 241(1):63–73
Zhou N, Fridley D, McNeil M et al (2011) Analysis of potential energy saving and \(\text{ CO }_2\) emission reduction of home appliances and commercial equipments in China. Energy Policy 39(8):4541–4550
Zhu Q, Sarkis J, Lai K (2007) Initiatives and outcomes of green supply chain management implementation by Chinese manufacturers. J Environ Manag 85(1):179–189
Acknowledgments
This work was supported by National Natural Foundation of China Nos. 61473204, 71371133, and Humanity and Social Science Youth Foundation of Ministry of Education of China No. 14YJCZH204.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that no conflicts of interest exists in this paper.
Appendix
Appendix
For simplification, the time argument is omitted in the Appendices.
1.1 Proof of Proposition 1
Let \(V^I\) denote the value function of the integrated channel. Taking the energy efficiency level evolution into account, the Hamilton-Jacobi-Bellman (HJB) equation for the whole supply chain is
Maximization of the right-hand side of the HJB equation with respect to p and u yields
Inserting (30) and (31) on the right-hand side of the HJB equation provides
Guided by the model’s linear-quadratic structure, we conjecture that the integrated channel value function is quadratic and given by
and follows from (33) that
Substituting (33) and (34) into (32) yields
Equating the coefficients of \(x^2, x\) on both sides of (35), we get the expressions of \(I_1, I_2\) shown in Proposition 1. Similarly, \(I_3\) is obtained as
Accordingly, the channel profit is given by
Inserting (35) into (1) produces a differential equation for the optimal energy efficiency level. Integrating the differential equation one obtains the trajectory in (10), where the steady-state energy efficiency level \(x^{I}_{\infty }\) is globally stable if and only if \(R_1>0\), i.e.,
1.2 Proof of Corollary 2
Note from Proposition 2 that the monotonicity of sales price depends on the relationship of \(x_0\) and \(x^I_\infty \), of which \(R_1>0\). Specifically, when \(x_0>x^I_\infty \), the sales price is monotonically decreasing with time, namely, skimming pricing; when \(x_0<x^I_\infty \), the sales price monotonically increases with time, namely, penetration pricing.
Since \(0<c_1<\frac{\gamma }{\beta }\) which is assumed to reflect operational inefficiency effect and to ensure a positive \(x^I_\infty \), we have \(0<x^I_\infty <\frac{\gamma \theta ^2(\alpha -\beta c_0)}{2\beta h\delta (\delta +\rho )-\theta ^2\gamma ^2}\).
As such, if \(x_0>\frac{\gamma \theta ^2(\alpha -\beta c_0)}{2\beta h\delta (\delta +\rho )-\theta ^2\gamma ^2}\), meaning that \(x_0>x^I_\infty \), a skimming pricing strategy is adopted.
However, if \(x_0<\frac{\gamma \theta ^2(\alpha -\beta c_0)}{2\beta h\delta (\delta +\rho )-\theta ^2\gamma ^2}\), there exists \(\widetilde{c}_1\) which satisfies that \(x_0=\frac{\theta ^2(\gamma -\beta \widetilde{c}_1)(\alpha -\beta c_0)}{2\beta h\delta (\delta +\rho )-\theta ^2(\gamma -\beta \widetilde{c}_1)^2}\). When \(0<c_1<\widetilde{c}_1\), one has \(x_0>x^I_\infty \), which implies a skimming pricing strategy; when \(\widetilde{c}_1<c_1<\frac{\gamma }{\beta }\), it is found that \(x_0<x^I_\infty \), implying a penetration pricing.
1.3 Proof of Proposition 3
To obtain a Stackelberg equilibrium, we first determine the retailer’s pricing strategy p as a function of the manufacturer’s decisions w and u. Let \(V_R^D, V_M^D\) denote the value functions for the retailer and the manufacturer. The retailer’s HJB equation can be specified as
The maximization with respect to p yields the retailer’s reaction function:
Anticipating the retailer’s response in (40), the manufacturer’s HJB equation is given by
Performing the maximization on the right-hand side with respect to w and u yields
Substituting the expression of w above into (40) produces
Substitute (42) and (43) into HJB equations (39) and (41), and assume the following quadratic value functions:
Following the same procedure as that in the proof of Proposition 1, the six Riccati equations that characterize the coefficients of the value functions \(A_i, B_i, i=1, 2, 3\) are determined by identification. The coefficients \(A_1, A_2\) are given in Proposition 3, and other coefficients are presented as follows.
Then, the equilibrium profits of the manufacturer, the retailer and the whole channel are
Similarly, the optimal time path of the energy efficiency level can be written as in (17), where the steady state \(x^{D}_{\infty }\) is globally stable if and only if \(R_2>0\), i.e.,
1.4 Proof of Proposition 5
Let \(V_R^C, V^C\) denote the value functions for the retailer and the manufacturer, respectively. The retailer’s HJB equation can be specified as
The equilibrium sales price is given below by maximizing the right-hand side of (48) with respect to p, i.e.,
The manufacturer’s optimization problem is given by
subject to the dynamic evolution of energy efficiency level (1).
The corresponding HJB equation is
Substituting (49) into (51), then maximizing the right-hand side with respect to u yields
Conjecture the following value functions:
By means of the procedure of the proof for Proposition 1, we have
Consequently, \(u^C=u^I, x^C=x^I, p^C=p^I\). These equilibrium strategies are identical with the integrated solutions.
Similarly, the profits of the manufacturer and retailer, \(J^C_M\), \(J^C_R\), are given by the value functions in (24) and (25), where
1.5 Proof of Proposition 6
According to (26), we have
i.e.,
Thus, k satisfies \(k>\rho (J_M^{D}-J_{M}^C(0))\).
Similarly, according to (27), we have \(k<\rho (J_R^C(0)-J_R^{D})\).
Let \(k_1=\rho (J_M^{D}-J_{M}^C(0)), k_2=\rho (J_R^C(0)-J_R^{D})\). It’s easy to verify that \(J_{M}^C(0)<0, J_M^{D}>0\), so \(k_1>0\). Also,
Consequently, k should satisfy \(\rho (J_M^{D}-J_{M}^C(0))<k<\rho (J_R^C(0)-J_R^{D})\).
Rights and permissions
About this article
Cite this article
Zhang, Q., Zhang, J. & Tang, W. Coordinating a supply chain with green innovation in a dynamic setting. 4OR-Q J Oper Res 15, 133–162 (2017). https://doi.org/10.1007/s10288-016-0327-x
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10288-016-0327-x