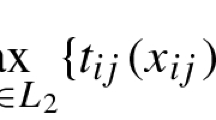An iterative solution technique for capacitated two-stage time minimization transportation problem

Abstract

Capacitated two-stage time minimization transportation problem is an important optimization problem arising in industries. In literature, there is only one approach to solving this problem, but it has a deficiency of resulting in memory overflow in implementation on computer for large scale instances. In this paper, this problem is reduced to a series of finding the feasible flow in a network with lower and upper arc capacities, and two iterative algorithms are proposed as more robust solution method for this problem as compared to the existing approach. It is proved that both iterative algorithms find the optimal solution to this problem in a polynomial time. Due to fully utilizing the network structure characteristics inherent to this problem, both iterative algorithms have the advantage of easy implementation on computer and high computational efficiency, and successfully overcome the deficiency of existing approach. Computational experiments validate that as compared to the existing approach, both iterative algorithms are efficient and more robust method to solve this problem, where one iterative algorithm significantly outperforms the other in terms of computational time, especially for large scale instances.

Appendices

Appendix A: The detailed proof of Lemma 3

To facilitate understanding the TMTP1-A algorithm, we present the theoretic basis for the TMTP1-A algorithm in the following. Without loss of generality, we assume that TMTP1 model has at least a feasible solution. Then for TMTP1 model, we create the following auxiliary model with controllable parameter, named as TMTP1(p), where controllable parameter p $\in \Omega$ = {1, 2, …, ω}.

$$ {\text{TMTP1(p)}}:\quad \left\{ \begin{gathered} {\text{Minimize}}\;{\text{z}}^{(1)} = \max \;\left\{ {\hat{t}_{ij} |(i,j) \in I \times J,x_{ij}^{(1)} > 0} \right\} \hfill \\ {\text{subject}}\;{\text{to}}\;\left\{ \begin{gathered} {\text{constraints}}\;{(1)} - {(4)}\;{\text{in}}\;{\text{C2TMTP}}\;{\text{model;}} \hfill \\ \forall i \in I\;{\text{and}}\;j \in J,\;if\;\hat{t}_{ij} > \alpha (p),\;then\;x_{ij}^{(1)} = 0. \hfill \\ \end{gathered} \right. \, \hfill \\ \end{gathered} \right. $$

Let “$x^{(1o)}$ = {$x_{ij}^{(1o)}$|$i \in I$, $j \in J$} as the first stage’s transportation scheme and $x^{(2o)}$ = {$x_{ij}^{(2o)}$|$i \in I$, $j \in J$} as the second stage’s transportation scheme” be the optimal solution of TMTP1 model. Let T_1min = max{$\hat{t}_{ij}$|$(i,j) \in I \times J$,$x_{ij}^{(1o)}$ $>$ 0} be the optimal objective function value of TMTP1 model as the first stage’s minimal feasible transportation time for C2TMTP model. From Proposition 2, it is derived that T_1min $>$ 0. Then there exists such unique p^o $\in \Omega$ that α(p^o) = T_1min. Hence, adopting the proof by contradiction, one can easily prove the following Proposition 3.

Proposition 3

The optimal solution of TMTP1 model is also the optimal solution of TMTP1(p ^o ) model, and vice versa. Furthermore, any feasible solution of TMTP1(p ^o ) model is the optimal solution of TMTP1 model.

Construct model set {TMTP1(p) model $|p \in \Omega$}. For any model in this model set, there is a feasible solution or not; if there is, then find the feasible solution and its corresponding objective function value. Then from Proposition 3, we derive the following Proposition 4.

Proposition 4

The minimum of all the objective function values corresponding to the feasible solutions found for all models in the model set {TMTP1(p) model $|p \in \Omega$ }is the optimal objective function value of TMTP1 model, and the found feasible solution corresponding to the minimal objective function value is the optimal solution of TMTP1 model.

Obviously, Proposition 4 gives a new idea to solve TMTP1 model. Moreover, it is easy to prove the following Proposition 5.

Proposition 5

There is one to one correspondence between the feasible flow in the network $G$ obtained in Step 2 of TMTP1-A and the feasible solution of current TMTP1(p) model. Furthermore, for p, p ^* $\in \Omega$ subject to p $<$ p ^* , if TMTP1(p) model has no feasible solution, then TMTP1(p ^* ) model surely has no feasible solution.

Utilizing Propositions 1 and 5 as well as Theorem 1, the TMTP1-A algorithm efficiently implements the new idea derived from Propositions 2–4 to solve TMTP1 model.

In fact, Steps 2 to 4 are the iterative process to gradually approach the optimal objective function value of TMTP1 model by calling the FFn-A algorithm at most ω times. Furthermore, each iteration is to judge whether there is a feasible flow in a network with lower and upper arc capacities, and find the flow matrix for the feasible flow if there is, by calling the FFn-A algorithm.

As per Lemma 2, Step 1 holds obviously. In Step 1, a strictly decreasing sequence “α(1), α(2), α(3), …, α(ω)” is obtained to control the iteration process of Steps 2 to 4; the upper arc matrix $\overline{C}$ for the network $G$ constructed as per Definition 1 is saved in the specific matrix C; the given bound ${\text{ z}}^{(b)}$ is initially set as positive infinity (i.e. + ∞); the controllable parameter p of TMTP1(p) model is initially set as one; and the indicator Fd, indicating if TMTP1 model’s feasible or optimal solution is found, is initially set as zero to indicate a feasible or optimal solution is not found.

Step 2 is to disconnect all the first stage’s flow-controlled arcs for the origin–destination routes with shipping time more than the given bound ${\text{ z}}^{(b)}$ in the network $G$ constructed as per Definition 1 to obtain a new network $G$ , by setting the upper capacities of all corresponding first stage’s flow-controlled arcs to be zero. It is known that in a network with lower and upper arc capacities, the arc with lower and upper capacities as zero does actually not exist or it can be regarded as a disconnected arc. Hence, Step 2 holds obviously.

Step 3 is actually to judge whether current TMTP1(p) model has a feasible solution, and if it has, then find the feasible solution “ $x^{(1)}$  = { $x_{ij}^{(1)}$ | $i \in I$ , $j \in J$ } as the first stage’s transportation scheme and $x^{(2)}$  = { $x_{ij}^{(2)}$ | $i \in I$ , $j \in J$ } as the second stage’s transportation scheme” and its corresponding objective function value ${\text{ z}}^{(1)}$ for current TMTP1(p) model, update the given bound ${\text{ z}}^{(b)}$ with the objective function value ${\text{ z}}^{(1)}$ found for current TMTP1(p) model, update the controllable parameter p of current TMTP1(p) model such that p $\in \Omega$ and α(p) =  ${\text{ z}}^{(b)}$ , increase TMTP1(p) model's controllable parameter p by one to use in next iteration, and set the indicator Fd as one to indicate the feasible or optimal solution is found, by calling the FFn-A algorithm to find the flow matrix $F = (F_{{ij}} )_{{n \times n}}$ for a feasible flow in the newly obtained network $G$ . Then, from Theorem 1 and Propositions 1 and 5 as well as the one to one correspondence between the flow matrix $F = (F_{{ij}} )_{{n \times n}}$ for a feasible flow in the newly obtained network $G$ and the feasible solution “ $x^{(1)}$ and $x^{(2)}$ ” of current TMTP1(p) model, it is derived that Step 3 holds.

Step 4 is to judge whether the iteration termination condition (i.e., the controllable parameter p of the TMTP1(p) model to be solved in next iteration is more than ω) is satisfied. So, Step 4 holds obviously.

From above analyses and explanations and Theorem 1, it is derived that Step 5 holds. Furthermore, the optimal objective function value and optimal solution for TMTP1 model are found as output in Step 5 if the optimal does exist.

Therefore, we conclude that Lemma 3 holds.

Appendix B: The proof of Lemma 4

The theoretic basis for the TMTP2-A algorithm is similar to that given in "Appendix A" for the TMTP1-A algorithm, and it is omitted for the sake of simplicity.

In fact, Steps 2 to 4 are the iterative process to judge whether TMTP2 model has a feasible solution, and if it has, then gradually approach the optimal objective function value of TMTP2 model, by calling the FFn-A algorithm at most ω times. Similarly to Lemma 3, it is easily derived from Theorem 1 and the above explanations that Lemma 4 holds.

Appendix C: The proof of Lemma 5

The theoretic basis for the TMTPu-A algorithm is also similar to that given in “Appendix A” for the TMTP1-A algorithm, and it is also omitted for the sake of simplicity.

In fact, Steps 2 to 4 are the iterative process to judge whether TMTP(Tu) model has a feasible solution, and if it has, then gradually approach its optimal objective function value, by calling the FFn-A algorithm at most ω times. Similarly to Lemma 3, it is easily derived from Theorem 1 and the above explanations that Lemma 5 holds.

Appendix D: The proof of Lemma 6

The theoretic basis for the TMTPp-A algorithm is also similar to that given in “Appendix A” for the TMTP1-A algorithm, and it is also omitted for the sake of simplicity.

In fact, Steps 2 to 4 are the iterative process to judge whether TMTP(z₁,z₂,α(p)) model has a feasible solution, and if it has, then gradually approach its optimal objective function value, by calling the FFn-A algorithm at most η times, where η is the number of distinct time values for all the elements in set {$\hat{t}_{ij}$|$(i,j) \in I \times J$, $\hat{t}_{ij} < z_{1} {\text{ + z}}_{2} - \alpha (p)$}. It is notable that η is no more than ω, and η = 0 when set {$\hat{t}_{ij}$|$(i,j) \in I \times J$, $\hat{t}_{ij} < z_{1} {\text{ + z}}_{2} - \alpha (p)$} is empty set. Similarly to Lemma 3, it is easily derived from Theorem 1 and the above explanations that Lemma 6 holds.

Appendix E: The detailed proof of Theorem 2

In fact, the idea of C2TMTP-A1 is as follows. Initially, solve TMTP1 model by calling TMTP1-A, to judge whether C2TMTP model has a feasible solution, and find TMTP1 model’s optimal objective function value T_1min as the first stage’s minimal feasible transportation time for C2TMTP model if it has. Next, on condition that C2TMTP model has a feasible solution, solve TMTP(Tu) model by setting controllable parameter Tu as positive infinity (+ ∞) and calling TMTPu-A, to generate the first pair for the first and second stage’s transportation time corresponding to a feasible solution of C2TMTP model, so that the second stage’s transportation time for the first pair is TMTP2 model’s optimal objective function value T_2min i.e. the second stage’s minimal feasible transportation time for C2TMTP model. Then, on condition that C2TMTP model has a feasible solution, iteratively solve TMTP(Tu) model by resetting controllable parameter Tu as the first stage’s transportation time for the pair found in recent iteration and calling TMTPu-A, to generate the next pair for the first and second stage’s transportation time corresponding to a feasible solution of C2TMTP model, so that the first stage’s transportation time for currently generated pair strictly decreases as compared to that for recently generated pair, until it is found that current TMTP(Tu) model has no feasible solution or the first stage’s transportation time corresponding to the optimal solution of current TMTP(Tu) model equals T_1min i.e. the first stage’s minimal feasible transportation time for C2TMTP model. Consequently, on condition that C2TMTP model has a feasible solution, a finite sequence for the first and second stage’s transportation time pairs is generated, so that in this sequence, the first stage’s transportation time for each pair strictly decreases, and the second stage’s transportation time for each pair monotonically increases, and the pair with minimal sum of the first and second stage’s transportation time corresponds to C2TMTP model’s optimal solution.

As per Lemma 3 and the fact that TMTP1 model has the same constraints as C2TMTP model, Step 1 holds. In Step 1, on condition that C2TMTP model has a feasible solution, the first stage’s minimal feasible transportation time for C2TMTP model, T_1min, is found by calling TMTP1-A, the controllable parameter Tu for TMTP(Tu) model is initially set as positive infinity (+ ∞), the iteration pointer k is initially set as zero, and the optimal objective function value $z^{(*)}$ for C2TMTP model is initially set as positive infinity (+ ∞).

When Step 2 is run for the first time, due to Tu =  + ∞ initially, TMTPu-A surely finds “$x^{(1)}$ = {$x_{ij}^{(1)}$|$i \in I$,$j \in J$} i.e. the first stage’s transportation scheme and $x^{(2)}$ = {$x_{ij}^{(2)}$|$i \in I$,$j \in J$} i.e. the second stage’s transportation scheme” as the optimal solution of current TMTP(Tu) model i.e. the optimal solution of TMTP2 model. Next, go to Step 3, and hence the first pair ($T_{1}^{p} (1)$,$T_{2}^{p} (1)$) for the first and second stage’s transportation time corresponding to a feasible solution of C2TMTP model is generated. Then, Step 4 is run for the first time, two cases arise. Case (a): $T_{1}^{p} (1)$ = T_1min; Case (b): $T_{1}^{p} (1)$ > T_1min. In Case (a), it is obvious that the first pair ($T_{1}^{p} (1)$,$T_{2}^{p} (1)$) gives the optimal objective function value and optimal solution for C2TMTP model, then go to Step 5 to output the result. In Case (b), repeat Step 2 for the updated $Tu = T_{1}^{p} (1)$.

When Step 2 is run for the second time, the following two cases arise. Case (c): TMTPu-A finds “$x^{(1)}$ = {$x_{ij}^{(1)}$|$i \in I$,$j \in J$} i.e. the first stage’s transportation scheme and $x^{(2)}$ = {$x_{ij}^{(2)}$|$i \in I$,$j \in J$} i.e. the second stage’s transportation scheme” as the optimal solution of current TMTP(Tu) model. Case (d): TMTPu-A finds that current TMTP(Tu) model has no feasible solution. In Case (c), go to Step 3, and hence the second pair ($T_{1}^{p} (2)$,$T_{2}^{p} (2)$) for the first and second stage’s transportation time corresponding to a feasible solution of C2TMTP model is generated; therefore, from the construction of current TMTP(Tu) model, it is derived that $T_{1}^{p} (2)$$<$$T_{1}^{p} (1)$ and $T_{2}^{p} (2)$ ≥ $T_{2}^{p} (1)$; then Step 4 is run for the second time. In Case (d), from the construction of TMTP(Tu) model, it is derived that for smaller Tu, TMTP(Tu) model has no feasible solution as well; then go to Step 5 to output the result.

From above observations, it is derived that on condition that C2TMTP model has a feasible solution, by repeating Step 2 at most ω times, C2TMTP-A1 generates such a finite sequence for the first and second stage’s transportation time pair corresponding to a feasible solution of C2TMTP model as ($T_{1}^{p} (1)$,$T_{2}^{p} (1)$), ($T_{1}^{p} (2)$,$T_{2}^{p} (2)$), … , ($T_{1}^{p} (k)$,$T_{2}^{p} (k)$), …, ($T_{1}^{p} (K)$,$T_{2}^{p} (K)$). Furthermore, for any $T_{3}^{\Delta }$, it holds that $T_{1}^{p} (k + 1)$$<$$T_{1}^{p} (k)$ and $T_{2}^{p} (k + 1)$ ≥ $T_{2}^{p} (k)$. Therefore, we have inequalities (e): $T_{1}^{p} (1)$$>$$T_{1}^{p} (2)$$>$…$>$$T_{1}^{p} (k)$$>$…$>$$T_{1}^{p} (K - 1)$$>$$T_{1}^{p} (K)$ as well as inequalities (f): $T_{2}^{p} (1)$ ≤ $T_{2}^{p} (2)$ ≤ … ≤ $T_{2}^{p} (k)$ ≤ … ≤ $T_{2}^{p} (K - 1)$ ≤ $T_{2}^{p} (K)$.

Next, we prove that $z^{(*)}$ = min {$T_{1}^{p} (k)$ + $T_{2}^{p} (k)$| k = 1, 2, …, K}, where $z^{(*)}$ is the optimal objective function value of C2TMTP model.

Suppose that there is such a feasible solution “$x^{(\Delta 1)}$ = {$x_{ij}^{(\Delta 1)}$|$i \in I$,$j \in J$} i.e. the first stage’s transportation scheme and $x^{(\Delta 2)}$ = {$x_{ij}^{(\Delta 2)}$|$i \in I$,$j \in J$} i.e. the second stage’s transportation scheme” for C2TMTP model that $T_{1}^{\Delta }$ = max{$\hat{t}_{ij}$|$(i,j) \in I \times J$,$x_{ij}^{(\Delta 1)}$ $>$ 0}, $T_{2}^{\Delta }$ = max{$\hat{t}_{ij}$|$(i,j) \in I \times J$,$x_{ij}^{(\Delta 2)}$ $>$ 0}, and $T_{1}^{\Delta }$ $+$ $T_{2}^{\Delta }$ $<$ min{$T_{1}^{p} (k)$$+$$T_{2}^{p} (k)$| k = 1, 2, …, K}.

From inequalities (e), it is derived that for $T_{1}^{\Delta }$, there are three cases (i.e., Cases (I) to (III)) below.

Case (I) $T_{1}^{\Delta }$ ≥ $T_{1}^{p} (1)$.

In this case, since $T_{1}^{\Delta }$ $+$ $T_{2}^{\Delta }$ $<$ min{$T_{1}^{p} (k)$$+$$T_{2}^{p} (k)$| k = 1, 2, …, K}, we have $T_{1}^{\Delta }$$+$$T_{2}^{\Delta }$$<$$T_{1}^{p} (1)$$+$$T_{2}^{p} (1)$. Furthermore, from $T_{1}^{\Delta }$ ≥ $T_{1}^{p} (1)$ and $T_{1}^{\Delta }$$+$$T_{2}^{\Delta }$$<$$T_{1}^{p} (1)$$+$$T_{2}^{p} (1)$, it is derived that $T_{2}^{\Delta }$$<$$T_{2}^{p} (1)$. Then the TMTP(Tu) model with Tu =  + ∞ has such a feasible solution “$x^{(\Delta 1)}$ and $x^{(\Delta 2)}$” that $T_{2}^{\Delta }$$<$$T_{2}^{p} (1)$, contradicting to the optimality of $T_{2}^{p} (1)$ = T_2min as the second stage’s minimal feasible transportation time for C2TMTP model.

Case (II) $T_{1}^{\Delta }$$<$$T_{1}^{p} (K)$.

In this case, it is easy to know that “$x^{(\Delta 1)}$ and $x^{(\Delta 2)}$” is a feasible solution of the TMTP(Tu) model with $Tu = T_{1}^{p} (K)$. However, since the pair ($T_{1}^{p} (K)$,$T_{2}^{p} (K)$) generated by C2TMTP-A1 is the last pair in the generated sequence of the first and second stage’s transportation time pair corresponding to a feasible solution of C2TMTP model, it is derived from C2TMTP-A1’s flow process that the TMTP(Tu) model with $Tu = T_{1}^{p} (K)$ has no feasible solution, contradicting to the known result that the TMTP(Tu) model with $Tu = T_{1}^{p} (K)$ has the feasible solution as “$x^{(\Delta 1)}$ and $x^{(\Delta 2)}$”.

Case (III) $T_{1} ^{p} (K) \le T_{1}^{\Delta } < T_{1} ^{p} (1)$

In this case, from inequalities (e), we derive there is such $\bar{k} \in \{ 2,3, \ldots ,K\}$ that $T_{1}^{p} (\overline{k})$ ≤ $T_{1}^{\Delta }$$<$$T_{1}^{p} (\overline{k} - 1)$. From $T_{1}^{\Delta }$ $+$ $T_{2}^{\Delta }$ $<$ min {$T_{1}^{p} (k)$$+$$T_{2}^{p} (k)$| k = 1, 2, …, K}, it is derived that $T_{1}^{\Delta }$$+$$T_{2}^{\Delta }$$<$$T_{1}^{p} (\overline{k})$$+$$T_{2}^{p} (\overline{k})$. Furthermore, from $T_{1}^{p} (\overline{k})$ ≤ $T_{1}^{\Delta }$ and $T_{1}^{\Delta }$$+$$T_{2}^{\Delta }$$<$$T_{1}^{p} (\overline{k})$$+$$T_{2}^{p} (\overline{k})$, it is derived that $T_{2}^{\Delta }$$<$$T_{2}^{p} (\overline{k})$. Then the TMTP(Tu) model with $Tu = T_{1} ^{p} (\bar{k} - 1)$ has a feasible solution “$x^{(\Delta 1)}$ and $x^{(\Delta 2)}$” with corresponding objective function value as $T_{2}^{\Delta }$ less than $T_{2}^{p} (\overline{k})$, contradicting to the optimality of $T_{2}^{p} (\overline{k})$ as the optimal objective function value of the TMTP(Tu) model with $Tu = T_{1} ^{p} (\bar{k} - 1)$.

Moreover, it is observed that C2TMTP-A1 first solves TMTP1 model by calling TMTP1-A, and then performs K iterations, where each iteration is to solve TMTP(Tu) model by calling TMTPu-A. Hence, the time complexity of C2TMTP-A1 is O(T₁ $+$ KT_c), where T₁ is the computational time for TMTP1-A to solve TMTP1 model, K is the number of iterations, and T_c is the computational time for TMTPu-A to solve TMTP(Tu) model. Since K is no more than ω, we derive that the time complexity O(T₁ $+$ KT_c) for C2TMTP-A1 is no more than O(T₁ $+$ ωT_c). From Lemmas 3 and 5, it is derived that TMTP1-A and TMTPu-A are polynomial time algorithm. Therefore, C2TMTP-A1 is polynomial time algorithm.

From the above analyses as well as Lemmas 3 and 5, it is derived that Theorem 2 holds (Ahuja et al. 1993).

Appendix F: The detailed proof of Theorem 3

Actually, the idea of C2TMTP-A2 is as follows. First, solve TMTP1 model by calling TMTP1-A, to judge whether C2TMTP model has a feasible solution, and find TMTP1 model’s optimal objective function value T_1min as the first stage’s minimal feasible transportation time for C2TMTP model if it has. Next, on condition that C2TMTP model has a feasible solution, solve TMTP2 model by calling TMTP2-A, to generate the first pair for the first and second stage’s transportation time corresponding to a feasible solution of C2TMTP model, so that the second stage’s transportation time for the first pair is TMTP2 model’s optimal objective function value T_2min i.e. the second stage’s minimal feasible transportation time for C2TMTP model. Then, on condition that C2TMTP model has a feasible solution, by calling TMTPp-A, iteratively solve the TMTP(z₁,z₂,α(p)) model with controllable parameters z₁ and z₂ as the first and second stage’s transportation time respectively in the recently obtained pair but controllable parameter p initially set as one plus such p that α(p) = z₁ then sequentially increased by one till α(p) = T_1min, to generate the next pair for the first and second stage’s transportation time corresponding to a feasible solution of C2TMTP model as early as possible, until TMTPp-A finds that all the TMTP(z₁,z₂,α(p)) models with “T_1min ≤ α(p)$<$ z₁” have no feasible solution, or the first stage’s transportation time for the currently generated pair equals T_1min i.e. the first stage’s minimal feasible transportation time for C2TMTP model. Consequently, on condition that C2TMTP model has a feasible solution, a finite sequence for the first and second stage’s transportation time pairs is generated, so that in this sequence, the first stage’s transportation time for each pair strictly decreases, the sum of the first and second stage’s transportation time for each pair strictly decreases as well, and the last pair corresponds to C2TMTP model’s optimal solution.

As per Lemma 3 and the fact that TMTP1 model has the same constraints as C2TMTP model, Step 1 holds. In Step 1, a strictly decreasing sequence α(1), α(2),…,α(ω) is produced by sorting the shipping times of all origin–destination routes with equal elements regarded as one element; whether C2TMTP model has a feasible solution is judged by TMTP1-A; and on condition that C2TMTP model has a feasible solution, TMTP1 model’s optimal objective function value T_1min is found (by TMTP1-A) as the first stage’s minimal feasible transportation time for C2TMTP model, sequence location indicator pT_1min for iteration termination is found in set $\Omega$ = {1, 2, …, ω} so that α(pT_1min) = T_1min, and iteration pointer k is set as one.

As per Lemma 4, Step 2 holds. In Step 2, the first pair ($\, T_{1} (1)$,$\, T_{2} (1)$) for the first and second stage’s transportation time corresponding to TMTP2 model’s optimal solution as C2TMTP model’s feasible solution is generated, and current sequence location indicator p is found in set $\Omega$ so that α(p) = $\, T_{1} (1)$.

When Step 3 is run for the first time, the following two cases (i.e. Case (1) and Case (2)) arise. Case (1): p = pT_1min. Case (2): p < pT_1min. In Case (1), it is obvious that the first pair ($\, T_{1} (1)$,$\, T_{2} (1)$) for the first and second stage’s transportation time found in Step 2 surely corresponds to the optimal solution of C2TMTP model; furthermore, at this point, the found in Step 2 as “$x^{(o1)}$ = {$x_{ij}^{(o1)}$|$i \in I$,$j \in J$} i.e. the first stage’s transportation scheme and $x^{(o2)}$ = {$x_{ij}^{(o2)}$|$i \in I$,$j \in J$} i.e. the second stage’s transportation scheme” is surely the optimal solution of C2TMTP model, and the found in step 2 as ${\text{ z}}^{(o)}$ is surely the optimal objective function value of C2TMTP model; hence, go to Step 5 to output the result. In Case (2), as initialization, TMTP(z₁,z₂,α(p)) model’s controllable parameters z₁ and z₂ are set as $\, T_{1} (1)$ and $\, T_{2} (1)$ respectively, and go to Step 4.

When Step 4 is run for the first time, as initialization, TMTP(z₁,z₂,α(p)) model’s controllable parameter p as current sequence location indicator is increased by one (i.e. let p = p + 1); next, call TMTPp-A to solve current TMTP(z₁,z₂,α(p)) model, then the following two cases [i.e. Case (3) and Case (4)] arise. Case (3): The TMTPp-A algorithm finds the optimal solution “$x^{(1)}$ = {$x_{ij}^{(1)}$|$i \in I$,$j \in J$} i.e. the first stage’s transportation scheme and $x^{(2)}$ = {$x_{ij}^{(2)}$|$i \in I$,$j \in J$} i.e. the second stage’s transportation scheme” for current TMTP(z₁,z₂,α(p)) model. Case (4): The TMTPp-A algorithm finds that current TMTP(z₁,z₂,α(p)) model has no feasible solution. In Case (3), the second pair ($\, T_{1} (2)$,$\, T_{2} (2)$) for the first and second stage’s transportation time, corresponding to current TMTP(z₁,z₂,α(p)) model’s optimal solution as C2TMTP model’s feasible solution, is generated so that $\, T_{1} (2)$$<$$\, T_{1} (1)$ and $\, T_{1} (2)$$+$$\, T_{2} (2)$$<$$\, T_{1} (1)$$+$$\, T_{2} (1)$ due to the construction of current TMTP(z₁,z₂,α(p)) model as well as α(p)$<$$\, T_{1} (1)$ at this moment (because the sequence {α(p)} is strictly decreasing), then repeat Step 3 for the updated current sequence location indicator p such that p belongs to set $\Omega$ and α(p) = $\, T_{1} (2)$. In Case (4), two sub-cases (i.e. Sub-case (4.1) and Sub-case (4.2)) arise. Sub-case (4.1): p $<$ pT_1min. Sub-case (4.2): p = pT_1min. In Sub-case (4.1), repeat Step 4. In Sub-case (4.2), jump out of the loop in Step 4, and go to Step 5 to output the result.

From above observations, it is derived that on condition that C2TMTP model has a feasible solution, by calling TMTPp-A to solve TMTP(z₁,z₂,α(p)) model no more than ω times, C2TMTP-A2 generates such a finite sequence for the first and second stage’s transportation time pair corresponding to a feasible solution of C2TMTP model as ($T_{1} (1)$, $T_{2} (1)$), ($T_{1} (2)$,$T_{2} (2)$),…,($T_{1} (k)$,$T_{2} (k)$),…,($T_{1} (L)$,$T_{2} (L)$). Furthermore, for any $k \in \{ 1,2, \ldots ,L - 1\}$, it holds that $\, T_{1} (k + 1)$$<$$\, T_{1} (k)$ and $\, T_{1} (k + 1)$$+$$\, T_{2} (k + 1)$$<$$\, T_{1} (k)$$+$$\, T_{2} (k)$. Therefore, we have obtained inequalities (7): $T_{1} (1)$$>$$T_{1} (2)$$>$…$>$$T_{1} (k)$ $>$…$>$$T_{1} (L - 1)$$>$$T_{1} (L)$ as well as inequalities (8):$\, T_{1} (1)$$+$$\, T_{2} (1)$$>$$\, T_{1} (2)$$+$$\, T_{2} (2)$$>$…$>$$\, T_{1} (k)$$+$$\, T_{2} (k)$$>$…$>$ $\, T_{1} (L - 1)$$+$$\, T_{2} (L - 1)$$>$$T_{1} (L)$$+$$T_{2} (L)$.

Next, we prove that ${\text{ z}}^{(o)}$ = $T_{1} (L)$$+$$T_{2} (L)$, where ${\text{ z}}^{(o)}$ is the optimal objective function value of C2TMTP model.

Suppose that there is a feasible solution as “$x^{(1*)}$ = {$x_{ij}^{(1*)}$|$i \in I$,$j \in J$} i.e. the first stage’s transportation scheme and $x^{(2*)}$ = {$x_{ij}^{(2*)}$|$i \in I$,$j \in J$} i.e. the second stage’s transportation scheme” for C2TMTP model such that $T_{1}^{*}$ = max{$\hat{t}_{ij}$|$(i,j) \in I \times J$,$x_{ij}^{(1*)}$ $>$ 0}, $T_{2}^{*}$ = max{$\hat{t}_{ij}$|$(i,j) \in I \times J$,$x_{ij}^{(2*)}$ $>$ 0}, and $T_{1}^{*}$$+$$T_{2}^{*}$$<$$T_{1} (L)$$+$$T_{2} (L)$.

From inequalities (7), it is derived that for $T_{1}^{*}$, there are three cases [i.e. Cases (9) to (11)] below.

Case (9) $T_{1}^{*}$ ≥ $T_{1} (1)$.

In this case, since $T_{1}^{*}$$+$$T_{2}^{*}$$<$$T_{1} (L)$$+$$T_{2} (L)$ and $T_{1} (L)$$+$$T_{2} (L)$$<$$\, T_{1} (1)$$+$$\, T_{2} (1)$ [see inequalities (8)], we have $T_{1}^{*}$$+$$T_{2}^{*}$$<$$\, T_{1} (1)$$+$$\, T_{2} (1)$. Hence, from $T_{1}^{*}$ ≥ $T_{1} (1)$ and $T_{1}^{*}$$+$$T_{2}^{*}$$<$$\, T_{1} (1)$$+$$\, T_{2} (1)$, it is derived that $T_{2}^{*}$$<$$\, T_{2} (1)$. Then TMTP2 model has such a feasible solution “$x^{(1*)}$ and $x^{(2*)}$” that $T_{2}^{*}$$<$$\, T_{2} (1)$, contradicting to the optimality of $\, T_{2} (1)$ for TMTP2 model.

Case (10) $T_{1}^{*}$$<$$T_{1} (L)$.

In this case, it is easily known that “$x^{(1*)}$ and $x^{(2*)}$” is a feasible solution for the TMTP(z₁,z₂,α(p)) model with “z₁ = $T_{1} (L)$, z₂ = $T_{2} (L)$, and p is in set $\Omega$ subject to T_1min ≤ α(p) = $T_{1}^{*}$$<$$T_{1} (L)$”. Whereas, because the pair ($T_{1} (L)$,$T_{2} (L)$) generated by C2TMTP-A2 is the last pair in the generated sequence for the first and second stage’s transportation time pairs, we derive that all the TMTP(z₁,z₂,α(p)) models with “z₁ = $T_{1} (L)$, z₂ = $T_{2} (L)$, and p is in set $\Omega$ subject to T_1min ≤ α(p)$<$$T_{1} (L)$” have no feasible solution, contradicting to the known result that “$x^{(1*)}$ and $x^{(2*)}$” is a feasible solution for the TMTP(z₁,z₂,α(p)) model with “z₁ = $T_{1} (L)$, z₂ = $T_{2} (L)$, and p is in set $\Omega$ subject to T_1min ≤ α(p) = $T_{1}^{*}$$<$$T_{1} (L)$”.

Case (11) $T_{1} (L)$ ≤ $T_{1}^{*}$$<$$T_{1} (1)$.

In this case, from inequalities (7), we derive there is such $\overline{k} \in \{ 2,3, \ldots ,L\}$ that $T_{1} (\overline{k})$ ≤ $T_{1}^{ * }$$<$$T_{1} (\overline{k} - 1)$. First, from $T_{1}^{*}$$+$$T_{2}^{*}$$<$$T_{1} (L)$$+$$T_{2} (L)$ and inequalities (8), it is acquired that $T_{1}^{*}$$+$$T_{2}^{*}$$<$$T_{1} (\overline{k})$$+$$T_{2} (\overline{k})$. Next, from $T_{1} (\overline{k})$ ≤ $T_{1}^{ * }$ and $T_{1}^{*}$$+$$T_{2}^{*}$$<$$T_{1} (\overline{k})$$+$$T_{2} (\overline{k})$, it is derived that $T_{2}^{*}$$<$$T_{2} (\overline{k})$. Then, from C2TMTP-A2’s flow process, it is known that the TMTP(z₁,z₂,α(p)) model with “z₁ = $T_{1} (\overline{k} - 1)$, z₂ = $T_{2} (\overline{k} - 1)$, p = $\overline{p}$ is in set $\Omega$ subject to T_1min ≤ α($\overline{p}$) = $T_{1} (\overline{k})$ $<$$T_{1} (\overline{k} - 1)$” has a feasible solution with optimal objective function value as $T_{2} (\overline{k})$, and there is the optimality of $\overline{p}$, that is to say, $\overline{p}$ is such minimal p that the TMTP(z₁,z₂,α(p)) model with “z₁ = $T_{1} (\overline{k} - 1)$, z₂ = $T_{2} (\overline{k} - 1)$, and p is in set $\Omega$ subject to T_1min ≤ α(p) $<$$T_{1} (\overline{k} - 1)$” has a feasible solution. Moreover, it is known that the TMTP(z₁,z₂,α(p)) model with “z₁ = $T_{1} (\overline{k} - 1)$, z₂ = $T_{2} (\overline{k} - 1)$, and p = p^* is in set $\Omega$ subject to T_1min ≤ α(p^*) = $T_{1}^{ * }$$<$$T_{1} (\overline{k} - 1)$” has a feasible solution “$x^{(1*)}$ and $x^{(2*)}$” with $T_{2}^{*}$$<$$T_{2} (\overline{k})$. Since the sequence “α(1), α(2),…,α(ω)” is strictly decreasing, and α($\overline{p}$) = $T_{1} (\overline{k})$ ≤ $T_{1}^{ * }$ = α(p^*), it is derived that p^* ≤ $\overline{p}$. Furthermore, from the optimality of $\overline{p}$, it is derived that $\overline{p}$ ≤ p^*; and hence p^* = $\overline{p}$. Then, for the TMTP(z₁,z₂,α(p)) model with “z₁ = $T_{1} (\overline{k} - 1)$, z₂ = $T_{2} (\overline{k} - 1)$, and p = $\overline{p}$ is in set $\Omega$ subject to α($\overline{p}$) = $T_{1} (\overline{k})$$<$$T_{1} (\overline{k} - 1)$”, there is a feasible solution “$x^{(1*)}$ and $x^{(2*)}$” with objective function value as $T_{2}^{*}$ less than $T_{2} (\overline{k})$, contradicting to the optimality of $T_{2} (\overline{k})$.

Moreover, it is observed that C2TMTP-A2 first solves TMTP1 model by calling TMTP1-A, next solves TMTP2 model by calling TMTP2-A, and then performs L − 1 iterations, where each iteration is to solve TMTP(z₁,z₂,α(p)) model by calling TMTPp-A. Hence, the time complexity for C2TMTP-A2 is O(T₁ + T₂ + (L − 1)T_z), where T₁ is the computational time for TMTP1-A to solve TMTP1 model, T₂ is the computational time for TMTP2-A to solve TMTP2 model, L − 1 is the number of iterations, and T_z is the computational time for TMTPp-A to solve TMTP(z₁,z₂,α(p)) model. Since L − 1 is no more than ω, it is derived that the time complexity O(T₁ + T₂ + (L − 1)T_z) for C2TMTP-A2 is no more than O(T₁ + T₂ + ωT_z). From Lemmas 3 and 4 and 6, it is derived that TMTP1-A, TMTP2-A and TMTPp-A are polynomial time algorithm. Therefore, C2TMTP-A2 is polynomial time algorithm as well.

From the above analyses as well as Lemmas 3 and 4 and 6, it derived that Theorem 3 holds (Ahuja et al. 1993).