Skip to main content
SpringerLink
Log in

Geometric integration of non-autonomous linear Hamiltonian problems

  • Published:
Advances in Computational Mathematics Aims and scope Submit manuscript

Abstract

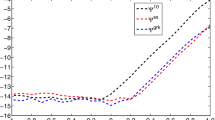
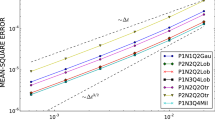
Symplectic integration of autonomous Hamiltonian systems is a well-known field of study in geometric numerical integration, but for non-autonomous systems the situation is less clear, since symplectic structure requires an even number of dimensions. We show that one possible extension of symplectic methods in the autonomous setting to the non-autonomous setting is obtained by using canonical transformations. Many existing methods fit into this framework. We also perform experiments which indicate that for exponential integrators, the canonical and symmetric properties are important for good long time behaviour. In particular, the theoretical and numerical results support the well documented fact from the literature that exponential integrators for non-autonomous linear problems have superior accuracy compared to general ODE schemes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Abraham, R., Marsden, J.E.: Foundations of mechanics Advanced Book Program, Reading, Mass. 2nd edn. Benjamin/Cummings Publishing Co. Inc (1978). http://resolver.caltech.edu/CaltechBOOK:1987.001

  2. Arnol’d, V.I.: Mathematical methods of classical mechanics Graduate Texts in Mathematics. 2nd edn., vol. 60. Springer, New York (1989), doi:10.1007/978-1-4757-2063-1

  3. Asorey, M., Cariñena, J.F., Ibort, A.: Generalized canonical transformations for time-dependent systems. J. Math. Phys. 24(12), 2745–2750 (1983). doi: 10.1063/1.525672

    Article  MathSciNet  MATH  Google Scholar 

  4. Blanes, S., Casas, F., Oteo, J.A., Ros, J.: Magnus and Fer expansions for matrix differential equations: the convergence problem. J. Phys. A 31(1), 259–268 (1998). doi:10.1088/0305-4470/31/1/023

    Article  MathSciNet  MATH  Google Scholar 

  5. Blanes, S., Casas, F., Oteo, J.A., Ros, J.: The Magnus expansion and some of its applications. Phys. Rep. 470(5–6), 151–238 (2009). doi: 10.1016/j.physrep.2008.11.001

    Article  MathSciNet  Google Scholar 

  6. Blanes, S., Diele, F., Marangi, C., Ragni, S.: Splitting and composition methods for explicit time dependence in separable dynamical systems. J. Comput. Appl. Math. 235(3), 646–659 (2010). doi:10.1016/j.cam.2010.06.018

    Article  MathSciNet  MATH  Google Scholar 

  7. Celledoni, E., Marthinsen, A., Owren, B.: Commutator-free Lie group methods. Futur. Gener. Comput. Syst. 19(3), 341–352 (2003). doi:10.1016/S0167-739X(02)00161-9

    Article  Google Scholar 

  8. Celledoni, E., McLachlan, R.I., Owren, B., Quispel, G.R.W.: Geometric properties of Kahan’s method. J. Phys. A 46(2), 025,201, 12 (2013). doi:10.1088/1751-8113/46/2/025201

    Article  MathSciNet  MATH  Google Scholar 

  9. Feng, K, Qin, M.Z.: The symplectic methods for the computation of Hamiltonian equations. In: Numerical Methods for Partial Differential Equations (Shanghai, 1987), Lecture Notes in Math. doi:10.1007/BFb0078537, vol. 1297, pp 1–37. Springer, Berlin (1987)

  10. Fer, F.: Résolution de l’équation matricielle d U/d t=p U par produit infini d’exponentielles matricielles. Acad. R Belg. Bull. Cl Sci. (5) 44, 818–829 (1958)

    MathSciNet  MATH  Google Scholar 

  11. González, C.J., Thalhammer, M.: A second-order Magnus-type integrator for quasi-linear parabolic problems. Math. Comput. 76(257), 205–231 (2007). doi: 10.1090/S0025-5718-06-01883-7

    Article  MathSciNet  MATH  Google Scholar 

  12. González, C.J., Ostermann, A., Thalhammer, M.: A second-order Magnus-type integrator for nonautonomous parabolic problems. J. Comput. Appl. Math. 189(1–2), 142–156 (2006). doi:10.1016/j.cam.2005.04.036

    Article  MathSciNet  MATH  Google Scholar 

  13. Grimm, V.K.R., Hochbruck, M.: Error analysis of exponential integrators for oscillatory second-order differential equations. J. Phys. A 39(19), 5495–5507 (2006). doi:10.1088/0305-4470/39/19/S10

    Article  MathSciNet  MATH  Google Scholar 

  14. Hairer, E., Wanner, G.: Solving Ordinary Differential Equations . II, Springer Series in Computational Mathematics, 2nd edn., vol. 14. Springer, Berlin (1996)

    Book  MATH  Google Scholar 

  15. Hairer, E., Nørsett, S.P., Wanner, G.: Solving Ordinary Differential Equations. I, Springer Series in Computational Mathematics, 2nd edn., vol. 8. Springer, Berlin (1993). doi:10.1007/978-3-540-78862-1

  16. Hairer, E., Lubich, C., Wanner, G.: Geometric Numerical Integration, 2nd edn.. Springer Series in Computational Mathematics, vol. 31. Springer, Berlin (2006). doi:10.1007/3-540-30666-8

  17. Hochbruck, M., Lubich, C.: On Magnus integrators for time-dependent Schrödinger equations. SIAM J. Numer. Anal. 41(3), 945–963 (2003). doi:10.1137/S0036142902403875

    Article  MathSciNet  MATH  Google Scholar 

  18. Iserles, A.: Solving linear ordinary differential equations by exponentials of iterated commutators. Numer. Math. 45(2), 183–199 (1984). doi:10.1007/BF01389464

    Article  MathSciNet  MATH  Google Scholar 

  19. Iserles, A.: On the global error of discretization methods for highly-oscillatory ordinary differential equations. BIT 42(3), 561–599 (2002). doi:10.1023/A:1022049814688

    Article  MathSciNet  MATH  Google Scholar 

  20. Iserles, A., Nørsett, S.P.: On the solution of linear differential equations in Lie groups. R Soc. Lond. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 357(1754), 983–1019 (1999). doi:10.1098/rsta.1999.0362

    Article  MathSciNet  MATH  Google Scholar 

  21. Khanamiryan, M.: Quadrature methods for highly oscillatory linear and non-linear systems of ordinary differential equations: part II. BIT 52(2), 383–405 (2012). doi:10.1007/s10543-011-0355-z

    Article  MathSciNet  MATH  Google Scholar 

  22. Leimkuhler, B.J., Reich, S.: Simulating Hamiltonian Dynamics. Cambridge Monographs on Applied and Computational Mathematics, vol. 14. Cambridge University Press, Cambridge (2004). doi:10.1017/CBO9780511614118

  23. Magnus, W.: On the exponential solution of differential equations for a linear operator. Commun. Pure Appl. Math. 7, 649–673 (1954). doi:10.1002/cpa.3160070404

    Article  MathSciNet  MATH  Google Scholar 

  24. Marsden, J.E., Ratiu, T.S.: Introduction to Mechanics and Symmetry, 2nd edn.. Texts in Applied Mathematics, vol. 17. Springer, New York (1999)

  25. Marthinsen, A., Owren, B.: Quadrature methods based on the Cayley transform. Appl. Numer. Math. 39(3–4), 403–413 (2001). doi:10.1016/S0168-9274(01)00087-3. special issue: Themes in geometric integration

    Article  MathSciNet  MATH  Google Scholar 

  26. Moler, C.B., Van Loan, C.F.: Nineteen dubious ways to compute the exponential of a matrix, twenty-five years later. SIAM Rev. 45(1), 3–49 (2003). doi:10.1137/S00361445024180

    Article  MathSciNet  MATH  Google Scholar 

  27. Ruth, R.D.: A canonical integration technique. IEEE Trans. Nucl. Sci. 30(4), 2669–2671 (1983). doi:10.1109/TNS.1983.4332919

    Article  Google Scholar 

  28. Struckmeier, J.: Hamiltonian dynamics on the symplectic extended phase space for autonomous and non-autonomous systems. J. Phys. A 38(6), 1257–1278 (2005). doi:10.1088/0305-4470/38/6/006

    Article  MathSciNet  MATH  Google Scholar 

  29. Suzuki, M.: Fractal decomposition of exponential operators with applications to many-body theories and Monte Carlo simulations. Phys. Lett. A 146(6), 319–323 (1990). doi:10.1016/0375-9601(90)90962-N

    Article  MathSciNet  Google Scholar 

  30. Yoshida, H.: Construction of higher order symplectic integrators. Phys. Lett. A 150(5–7), 262–268 (1990). doi:10.1016/0375-9601(90)90092-3

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematical Sciences, Norwegian University of Science and Technology (NTNU), 7491, Trondheim, Norway

    Håkon Marthinsen & Brynjulf Owren

Authors
  1. Håkon Marthinsen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Brynjulf Owren
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Håkon Marthinsen.

Additional information

Communicated by: Martin Stynes

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Marthinsen, H., Owren, B. Geometric integration of non-autonomous linear Hamiltonian problems. Adv Comput Math 42, 313–332 (2016). https://doi.org/10.1007/s10444-015-9425-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10444-015-9425-0

Keywords

Mathematics Subject Classification (2010)

Search

Navigation