Skip to main content
SpringerLink
Log in

On flexible block Chebyshev-Davidson method for solving symmetric generalized eigenvalue problems

  • Published:
Advances in Computational Mathematics Aims and scope Submit manuscript

Abstract

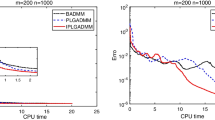
In a recent work (J. Sci. Comput. 85 (2020), no. 3), the author generalized the Chebyshev-Davidson method appeared in standard eigenvalue problems to symmetric generalized eigenvalue problems. The theoretical derivation indicates that the Chebyshev-Davidson method for symmetric generalized eigenvalue problems only admits local convergence; thus, in this paper, we adopt a flexible strategy to improve the global convergence and to save number of iteration steps. Moreover, the deflation technique used for computing several eigenpairs in the proposed Chebyshev-Davidson method cannot be implemented in parallel; therefore, we construct a flexible block Chebyshev-Davidson method for computing several eigenpairs of symmetric generalized eigenvalue problems. The block implementation is important in scientific computing since it allows parallelism and efficient use of local memory. Numerical experiments are carried out to show great superiority and robustness over some state-of-the-art iteration methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Data Availability

The data used to support the findings of this study are included within the article.

References

  1. Aishima, K.: Global convergence of the restarted Lanczos and Jacobi-Davidson methods for symmetric eigenvalue problems. Numer. Math. 131, 405–423 (2015)

    Article  MathSciNet  Google Scholar 

  2. Aishima, K.: On convergence of iterative projection methods for symmetric eigenvalue problems. J. Comput. Appl. Math. 311, 513–521 (2017)

    Article  MathSciNet  Google Scholar 

  3. Anderson, C.R.: A Rayleigh-Chebyshev procedure for finding the smallest eigenvalues and associated eigenvectors of large sparse Hermitian matrices. J. Comput. Phys. 229, 7477–7487 (2010)

    Article  MathSciNet  Google Scholar 

  4. Banerjee, A.S., Lin, L., Hu, W., Yang, C., Pask, J.E.: Chebyshev polynomial filtered subspace iteration in the discontinuous Galerkin method for large-scale electronic structure calculations. J. Chem. Phys. 15, 154101 (2016)

    Article  Google Scholar 

  5. Bekas, C., Kokiopoulou, E., Saad, Y.: Computation of large invariant subspaces using polynomial filtered Lanczos iterations with applications in density functional theory. SIAM J. Matrix Anal. Appl. 30, 397–418 (2008)

    Article  MathSciNet  Google Scholar 

  6. Bradbury, W.W., Fletcher, R.: New iterative methods for solution of the eigenproblem. Numer. Math. 9, 259–267 (1996)

    Article  MathSciNet  Google Scholar 

  7. Crouzeix, M., Philippe, B., Sadkane, M.: The Davidson method. SIAM J. Sci. Comput. 15, 62–76 (1994)

    Article  MathSciNet  Google Scholar 

  8. Davidson, E.R.: The iterative calculation of a few of the lowest eigenvalues and corresponding eigenvectors of large real-symmetric matrices. J. Comput. Phys. 17, 87–94 (1975)

    Article  MathSciNet  Google Scholar 

  9. Fang, H.R., Saad, Y.: A filtered Lanczos procedure for extreme and interior eigenvalue problems. SIAM J. Sci. Comput. 34, A2220–A2246 (2012)

    Article  MathSciNet  Google Scholar 

  10. Fokkema, D.R., Sleijpen, G.L.G., van der Vorst, H.A.: Jacobi-Davidson style QR and QZ algorithms for the reduction of matrix pencils. SIAM J. Sci. Comput. 20, 94–125 (1998)

    Article  MathSciNet  Google Scholar 

  11. Golub, G.H., Ye, Q.: An inverse free preconditioned Krylov subspace method for symmetric generalized eigenvalue problems. SIAM J. Sci. Copmut. 24, 312–334 (2002)

    Article  MathSciNet  Google Scholar 

  12. Hestenes, M.R., Karush, W.: A method of gradients for the calculation of the characteristic roots and vectors of a real symmetric matrix. J. Research Nat. Bur. Standards 47, 45–61 (1951)

    Article  MathSciNet  Google Scholar 

  13. Hetmaniuk, U., Lehoucq, R.: Basis selection in LOBPCG. J. Comput. Phys. 218, 324–332 (2006)

    Article  MathSciNet  Google Scholar 

  14. Jia, Z.-X.: A refined subspace iteration algorithm for large sparse eigenproblems. Appl. Numer. Math. 32, 35–52 (2000)

    Article  MathSciNet  Google Scholar 

  15. Jia, Z.-X., Stewart, G.W.: An analysis of the Rayleigh-Ritz method for approximating eigenspaces. Math. Comp. 70, 637–647 (2001)

    Article  MathSciNet  Google Scholar 

  16. Knyazev, A.V.: Toward the optimal preconditioned eigensolver: locally optimal block preconditioned conjugate gradient method. SIAM J. Sci. Comput. 23, 517–541 (2001)

    Article  MathSciNet  Google Scholar 

  17. Knyazev, A.V.: Hard and soft locking in iterative methods for symmetric eigenvalue problems. In: Presentation at the eighth copper mountain conference on iterative methods, (2004)

  18. Knyazev, A.V., Argentati, M.E., Lashuk, I., Ovtchinnikov, E.E.: Block locally optimal preconditioned eigenvalue xolvers (BLOPEX) in HYPRE and PETSc. SIAM J. Sci. Comput. 29, 2224–2239 (2007)

    Article  MathSciNet  Google Scholar 

  19. Li, R.-P., Xi, Y.-Z., Vecharynski, E., Yang, C., Saad, Y.: A thick-restart Lanczos algorithm with polynomial filtering for Hermitian eigenvalue problems. SIAM J. Sci. Comput. 38, A2512–A2534 (2016)

    Article  MathSciNet  Google Scholar 

  20. Miao, C.-Q.: Filtered Krylov-like sequence method for symmetric eigenvalue problems. Numer. Algorithms 82, 791–807 (2019)

    Article  MathSciNet  Google Scholar 

  21. Miao, C.-Q.: On Chebyshev-Davidson method for symmetric generalized eigenvalue problems. J. Sci. Comput. 85, (2020). https://doi.org/10.1007/s10915-020-01360-4

  22. Morgan, R.B.: Generalizations of Davidson’s method for computing eigenvalues of large nonsymmetric matrices. J. Comput. Phys. 101, 287–291 (1992)

    Article  MathSciNet  Google Scholar 

  23. Morgan, R.B., Scott, D.S.: Generalizations of Davidson’s method for computing eigenvalues of sparse symmetric matrices. SIAM J. Sci. Statisst. Copmut. 7, 817–825 (1986)

    MathSciNet  Google Scholar 

  24. Morgan, R.B., Scott, D.S.: Preconditioning the Lanczos algorithm for sparse symmetric eigenvalue problems. SIAM J. Sci. Comput. 14, 585–593 (1993)

    Article  MathSciNet  Google Scholar 

  25. Parlett, B.N.: The Symmetric Eigenvalue Problem. SIAM, Philadelphia, PA (1998)

    Book  Google Scholar 

  26. Saad, Y.: Chebyshev acceleration techniques for solving nonsymmetric eigenvalue problems. Math. Comp. 42, 567–588 (1984)

    Article  MathSciNet  Google Scholar 

  27. Saad, Y.: Numerical Methods for Large Eigenvalue Problems, 2nd edn. SIAM, Philadelphia, PA (2011)

    Book  Google Scholar 

  28. Sadkane, M.: A block Arnoldi-Chebyshev method for computing the leading eigenpairs of large sparse unsymmetric matrices. Numer. Math. 64, 181–193 (1993)

    Article  MathSciNet  Google Scholar 

  29. Sleijpen, G.L.G., Booten, A.G.L., Fokkema, D.R., van der Vorst, H.A.: Jacobi-Davidson type methods for generalized eigenproblems and polynomial eigenproblems. BIT Numer. Math. 36, 595–633 (1996)

    Article  MathSciNet  Google Scholar 

  30. Sleijpen, G.L.G., van der Vorst, H.A.: A Jacobi-Davidson iteration method for linear eigenvalue problems. SIAM J. Matrix Anal. Appl. 17, 401–425 (1996)

    Article  MathSciNet  Google Scholar 

  31. Sorensen, D.C.: Implicit application of polynomial filters in a k-step Arnoldi method. SIAM J. Matrix Anal. Appl. 13, 357–385 (1992)

    Article  MathSciNet  Google Scholar 

  32. Stathopoulos, A., McCombs, J.R.: PRIMME: preconditioned iterative multi-method eigensolver: methods and software description. ACM T. Math. Software 37, 21:1-21:30 (2010)

    Article  Google Scholar 

  33. Vecharynski, E., Yang, C., Pask, J.E.: A projected preconditioned conjugate gradient algorithm for computing many extreme eigenpairs of a Hermitian matrix. J. Comput. Phys. 290, 73–89 (2015)

    Article  MathSciNet  Google Scholar 

  34. Zhou, Y.-K.: A block Chebyshev-Davidson method with inner-outer restart for large eigenvalue problems. J. Comput. Phys. 229, 9188–9200 (2010)

    Article  MathSciNet  Google Scholar 

  35. Zhou, Y.-K., Saad, Y.: A Chebyshev-Davidson algorithm for large symmetric eigenproblems. SIAM J. Matrix Anal. Appl. 29, 954–971 (2007)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors are very much indebted to the referees for their constructive comments and valuable suggestions, which greatly improved the original manuscript of this paper.

Author information

Authors and Affiliations

  1. Hunan Key Laboratory of Analytical Mathematics and Applications, School of Mathematics and Statistics, Central South University, Changsha, 410083, People’s Republic of China

    Cun-Qiang Miao

  2. School of Mathematics and Statistics, Hunan First Normal University, Changsha, 410205, People’s Republic of China

    Lan Cheng

Authors
  1. Cun-Qiang Miao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lan Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Lan Cheng.

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Additional information

Communicated by: Peter Benner

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supported by the National Natural Science Foundation of China (No. 11901361 and No. 12001048) and the Natural Science Foundation of Hunan Province (No. 2021JJ40708), P.R. China.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Miao, CQ., Cheng, L. On flexible block Chebyshev-Davidson method for solving symmetric generalized eigenvalue problems. Adv Comput Math 49, 78 (2023). https://doi.org/10.1007/s10444-023-10078-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10444-023-10078-4

Keywords

Mathematics Subject Classification (2010)

Search

Navigation