Market manipulation with outside incentives

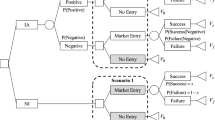
Abstract

Much evidence has shown that prediction markets can effectively aggregate dispersed information about uncertain future events and produce remarkably accurate forecasts. However, if the market prediction will be used for decision making, a strategic participant with a vested interest in the decision outcome may manipulate the market prediction to influence the resulting decision. The presence of such incentives outside of the market would seem to damage the market’s ability to aggregate information because of the potential distrust among market participants. While this is true under some conditions, we show that, if the existence of such incentives is certain and common knowledge, in many cases, there exist separating equilibria where each participant changes the market probability to different values given different private signals and information is fully aggregated in the market. At each separating equilibrium, the participant with outside incentives makes a costly move to gain trust from other participants. While there also exist pooling equilibria where a participant changes the market probability to the same value given different private signals and information loss occurs, we give evidence suggesting that two separating equilibria are more natural and desirable than many other equilibria of this game by considering domination-based belief refinement, social welfare, and the expected payoff of either participant in the game. When the existence of outside incentives is uncertain, however, trust cannot be established between players if the outside incentive is sufficiently large and we lose the separability at equilibria.

Appendices

Appendix 1: Proof of Proposition  1

Proof

The partial derivative of the loss function with respect to $r_A$ is

$$\begin{aligned} \frac{\partial }{\partial r_A} L(f_{s_A,\emptyset },r_A) = \frac{r_A - f_{s_A,\emptyset }}{r_A (1-r_A)}. \end{aligned}$$

(34)

It is negative for $r_A < f_{s_A,\emptyset }$, zero for $r_A = f_{s_A,\emptyset }$ and positive for $r_A > f_{s_A,\emptyset }$. Thus, the loss function is strictly increasing for $r_A \in [f_{s_A,\emptyset }, 1)$ and strictly decreasing for $r_A \in (0,f_{s_A,\emptyset }]$. In addition, note that $L(f_{s_A,\emptyset }, r_A) \rightarrow \infty$ as $r_A \rightarrow 0$ or $r_A \rightarrow 1$ for any fixed $f_{s_A,\emptyset }$. Hence, the loss function has the range $[0, \infty )$ for both $r_A \in [f_{s_A,\emptyset }, 1)$ and $r_A \in (0,f_{s_A,\emptyset }]$.

The partial derivative of the loss function with respect to $f_{s_A,\emptyset }$ is

$$\begin{aligned} \frac{\partial }{\partial {f_{s_A,\emptyset }}} L(f_{s_A,\emptyset },r_A) = \log \left( \frac{f_{s_A,\emptyset }}{1-f_{s_A,\emptyset }} \frac{1-r_A}{r_A}\right) . \end{aligned}$$

(35)

It equals zero when $f_{s_A,\emptyset } = r_A$, negative when $f_{s_A,\emptyset } < r_A$ and positive when $f_{s_A,\emptyset } > r_A$. Therefore, for a fixed $r_A \in [0,1]$, $L(f_{s_A,\emptyset },r_A)$ is strictly decreasing for $f_{s_A,\emptyset } \in [0, r_A]$ and strictly increasing for $f_{s_A,\emptyset } \in [r_A, 1]$. $\square$

Appendix 2: Example  1

Example 1

Suppose the outside payoff function is $Q(r_B) = r_B$, and the prior distribution is given by Table 2.

Table 2 An example prior distribution

It is easy to compute $f_{H,\emptyset } = 0.64$, $f_{T,\emptyset } = 0.54$, $f_{H,H} =1$, $f_{H,T} = 0.1$, $f_{T,H} = 0.9$, and $f_{T, T} = 0$.

Alice’s expected loss in MSR payoff when receiving the $T$ signal but changing the market probability to $f_{H,\emptyset }$ is

$$\begin{aligned} L(f_{T,\emptyset },f_{H,\emptyset })&= f_{T,\emptyset }\log \frac{f_{T,\emptyset }}{f_{H,\emptyset }} + (1-f_{T,\emptyset })\log \frac{1-f_{T,\emptyset }}{1-f_{H,\emptyset }}\nonumber \\&= \left( 0.54 \log \frac{0.54}{0.64} + 0.46 \log \frac{0.46}{0.36} \right) \approx 0.021. \end{aligned}$$

(36)

Alice’s expected gain in outside payoff when receiving the $T$ signal but convincing Bob that she has the $H$ signal is

$$\begin{aligned}&E_{S_B}[Q(f_{H,S_B}) - Q(f_{T,S_B}) \mid S_A = T] \nonumber \\&= \text {P}(S_B = H | S_A = T) (f_{H, H} - f_{T, H}) + \text {P}(S_B = T | S_A = T) (f_{H, T} - f_{T, T})\nonumber \\&= 0.6 (1 - 0.9) + 0.4 (0.1 - 0) \end{aligned}$$

(37)

$$\begin{aligned}&= 0.1. \end{aligned}$$

(38)

It is clear that $L(f_{T,\emptyset },f_{H,\emptyset }) <E_{S_B}[Q(f_{H,S_B}) - Q(f_{T,S_B}) \mid S_A = T]$. Thus, inequality (5) is satisfied and a truthful PBE does not exist.

In addition to the above derivation, we note that even though a truthful PBE does not exist for this example, a separating PBE does exist. The intuition behind this can be shown by calculating and comparing the quantities $Y_H$, $Y_T$, and $f_{H,\emptyset }$, as illustrated below. We solve for $Y_T$ by solving the following equation:

$$\begin{aligned} L(f_{T,\emptyset },Y_T)&= E_{S_B}[Q(f_{H,S_B}) - Q(f_{T,S_B}) \mid S_A = T] \end{aligned}$$

(39)

$$\begin{aligned}&\Rightarrow 0.54 \log \frac{0.54}{Y_T} + 0.46 \log \frac{0.46}{1 - Y_T} = 0.1 \end{aligned}$$

(40)

$$\begin{aligned}&\Rightarrow Y_T \approx 0.747 \end{aligned}$$

(41)

Similarly, we solve for $Y_H$ below:

$$\begin{aligned} L(f_{H,\emptyset },Y_H)&= E_{S_B}[Q(f_{H,S_B}) - Q(f_{T,S_B}) \mid S_A = H] \end{aligned}$$

(42)

$$\begin{aligned}&\Rightarrow 0.64 \log \frac{0.64}{Y_H} + 0.36 \log \frac{0.36}{1 - Y_H} = 0.1 \end{aligned}$$

(43)

$$\begin{aligned}&\Rightarrow Y_H \approx 0.827 \end{aligned}$$

(44)

The above calculations show that we have $f_{H,\emptyset } < Y_T < Y_H$. Thus, a truthful PBE does not exist because if Alice reports $f_{H,\emptyset }$ in the first stage, then Bob will believe that there is positive probability that Alice actually received a $T$ signal but is trying to pretend that she received a $H$ signal, since $f_{H,\emptyset } < Y_T$. However, since $Y_H > Y_T$, a separating equilibrium exists because Alice can establish credibility with Bob by reporting any value in $[Y_T, Y_H]$ in the first stage.

Lastly, note that this example illustrates a prior distribution for which the signals of Alice and Bob are independent. In Proposition 4, we will prove that when Alice and Bob have independent signals, $Y_H > Y_T$ must be satisfied. $\square$

Appendix 3: Proof of Proposition  3

Proof

If $f_{H,\emptyset } \ge Y_T \ge f_{T,\emptyset } \ge Y_{-T}$, then it is easy to see that $L(f_{H,\emptyset }, Y_T) \le L(f_{H,\emptyset }, Y_{-T})$ and the equality holds only when $Y_T = f_{T,\emptyset } = Y_{-T}$. The remainder of the proof focuses on the case when $f_{H,\emptyset } < Y_T$.

By definitions of $Y_T$ and $Y_{-T}$, we have

$$\begin{aligned} L(f_{T,\emptyset }, Y_T) = L(f_{T,\emptyset }, Y_{-T}). \end{aligned}$$

(45)

By Proposition 1 and $Y_{-T} \le f_{T,\emptyset } < f_{H,\emptyset }$, we have

$$\begin{aligned} L(f_{T,\emptyset }, Y_{-T}) < L(f_{H,\emptyset }, Y_{-T}). \end{aligned}$$

(46)

By Proposition 1 and $f_{T,\emptyset } < f_{H,\emptyset } \le Y_T$, we have

$$\begin{aligned} L(f_{H,\emptyset }, Y_{T}) < L(f_{T,\emptyset }, Y_{T}). \end{aligned}$$

(47)

Hence, we must have $L(f_{H,\emptyset }, Y_T) < L(f_{H,\emptyset }, Y_{-T})$ due to Eq. (45) and inequalities (46) and (47), as

$$\begin{aligned} L(f_{H,\emptyset }, Y_{T}) < L(f_{T,\emptyset }, Y_T) = L(f_{T,\emptyset }, Y_{-T}) < L(f_{H,\emptyset }, Y_{-T}). \end{aligned}$$

(48)

$\square$

Appendix 4: Example 2

Example 2

Consider the outside payoff function and the prior distribution in Table 3. We show below that there exists sufficiently small $\epsilon$ such that $Y_H < Y_T$.

Table 3 An example prior distribution with $\epsilon \in (0, 0.25)$

It is easy to compute $f_{H,\emptyset } = 4\epsilon$, $f_{T,\emptyset } = 2\epsilon$, $f_{H,H} =1$, $f_{H,T} = \frac{\epsilon }{0.5 - \epsilon }$, $f_{T,H} = \frac{\epsilon }{0.5 - \epsilon }$, and $f_{T, T} = 0$. With this, we can calculate

$$\begin{aligned} L(f_{H,\emptyset },Y_H)&= E_{S_B}[Q(f_{H,S_B})-Q(f_{T,S_B}) \mid S_A = H] \\&= \text {P}(S_B = H | S_A = H) (f_{H, H} - f_{T,H}) + \text {P}(S_B = T | S_A = H) (f_{H,T} - f_{T,T}) \\&= (2\epsilon ) \left( 1 - \frac{\epsilon }{0.5-\epsilon } \right) + (1 - 2\epsilon ) \left( \frac{\epsilon }{0.5-\epsilon } - 0 \right) . \end{aligned}$$

As $\epsilon$ approaches $0$, we have

$$\begin{aligned} \lim _{\epsilon \rightarrow 0} L(f_{H,\emptyset },Y_H) = 0. \end{aligned}$$

(49)

Because $\lim _{\epsilon \rightarrow 0} f_{H,\emptyset } = \lim _{\epsilon \rightarrow 0} 4 \epsilon =0,$ by definition of $L(f_{H,\emptyset },Y_H)$, (49) implies that

$$\begin{aligned} \lim _{\epsilon \rightarrow 0} Y_H = 0. \end{aligned}$$

(50)

Similarly, we have

$$\begin{aligned} L(f_{T,\emptyset },Y_T)&= E_{S_B}[Q(f_{H,S_B})-Q(f_{T,S_B}) \mid S_A = T] \\&= \text {P}(S_B = H | S_A = T) (f_{H, H} - f_{T,H}) + \text {P}(S_B = T | S_A = T) (f_{H,T} - f_{T,T}) \\&= (1-2\epsilon ) \left( 1 - \frac{\epsilon }{0.5-\epsilon } \right) + 2\epsilon \left( \frac{\epsilon }{0.5-\epsilon } - 0 \right) . \end{aligned}$$

As $\epsilon$ approaches $0$, we have

$$\begin{aligned} \lim _{\epsilon \rightarrow 0} L(f_{T,\emptyset },Y_T) = 1. \end{aligned}$$

(51)

Because $\lim _{\epsilon \rightarrow 0} f_{T,\emptyset } = \lim _{\epsilon \rightarrow 0} 2 \epsilon =0,$ by definition of $L(f_{T,\emptyset },Y_T)$,

$$\begin{aligned} \lim _{\epsilon \rightarrow 0} L(f_{T,\emptyset },Y_T) = - \log (1 - \lim _{\epsilon \rightarrow 0} Y_T). \end{aligned}$$

Given (51), we have

$$\begin{aligned} \lim _{\epsilon \rightarrow 0} Y_T = 1- 1/e. \end{aligned}$$

(52)

Combining (50) and (52), we know that when $\epsilon$ is sufficiently small, $Y_H < Y_T$.

In addition to the above derivation, we describe some qualitative properties of the given prior distribution, which may be helpful in highlighting the intuitions behind the $Y_H < Y_T$ condition. For this prior distribution, Alice is willing to report a higher value after receiving the $T$ signal due to the combined effect of two factors. First, note that when Alice has the $T$ signal, Bob is far more likely to have the $H$ signal than the $T$ signal for sufficiently small $\epsilon$. This is shown by

$$\begin{aligned} \lim _{\epsilon \rightarrow 0} \text {P}(S_B = H | S_A = T)&= \lim _{\epsilon \rightarrow 0} (1-2\epsilon ) = 1,\end{aligned}$$

(53)

$$\begin{aligned} \lim _{\epsilon \rightarrow 0} \text {P}(S_B = T | S_A = T)&= \lim _{\epsilon \rightarrow 0} 2\epsilon = 0. \end{aligned}$$

(54)

Second, Alice’s maximum gain in outside payoff when she has the $T$ signal but manages to convince Bob that she has the $H$ signal is much higher when Bob has the $H$ signal than when he has the $T$ signal for sufficiently small $\epsilon$. When Bob has the $H$ signal, the maximum gain for Alice is

$$\begin{aligned} \lim _{\epsilon \rightarrow 0} (f_{HH} - f_{TH}) = \lim _{\epsilon \rightarrow 0} (1 - \frac{\epsilon }{0.5-\epsilon }) = 1, \end{aligned}$$

(55)

which is greater than the maximum gain for Alice when Bob has the $T$ signal,

$$\begin{aligned} \lim _{\epsilon \rightarrow 0} (f_{HT} - f_{TT}) = \lim _{\epsilon \rightarrow 0} (\frac{\epsilon }{0.5-\epsilon } - 0) = 0. \end{aligned}$$

(56)

Thus, when Alice has the $T$ signal, Bob is more likely to have the $H$ signal, resulting in a higher expected gain in outside payoff for Alice by convincing Bob that she has the $H$ signal. This intuitively explains why $Y_T$ is high.

In Example 1, we describe a prior distribution and outside function and show that a truthful PBE does not exist when $f_{H,\emptyset } < Y_T \le Y_H$. Note that guaranteeing $f_{H,\emptyset } < Y_T \le Y_H$ is not the only way for a truthful PBE to fail to exist. For instance, this example shows that, when $f_{H,\emptyset } \le Y_H < Y_T$, a truthful PBE also fails to exist. $\square$

Appendix 5: Proof of Theorem 3

Proof

If $Y_T \ge f_{H,\emptyset }$, the interval $[\max (Y_{-H}, Y_T), Y_H]$ can be written as $[\max (f_{H,\emptyset }, Y_T), Y_H]$ because $Y_{-H} \le f_{H,\emptyset }$. If $Y_T < f_{H,\emptyset }$, the interval $[\max (Y_{-H}, Y_T), Y_H]$ can be split into two intervals $[\max (Y_{-H}, Y_T), f_{H,\emptyset })$ and $[\max (f_{H,\emptyset }, Y_T), Y_H]$. In the following, we first consider the case $r_A \in [\max (f_{H,\emptyset }, Y_T), Y_H]$; then, for $Y_T < f_{H,\emptyset }$, we consider the case $r_A \in [\max (Y_{-H}, Y_T), f_{H,\emptyset })$.

First, suppose that Alice reports $r_A \in [\max (f_{H,\emptyset }, Y_T), Y_H]$ after receiving the $H$ signal. Fix a particular $k \in [\max (f_{H,\emptyset }, Y_T), Y_H]$. We prove that the following pair of Alice’s strategy and Bob’s belief forms a separating PBE of our game:

$$\begin{aligned} SE_2(k): \left\{ \begin{array}{l} \sigma ^S_H(k) = 1, \sigma ^S_T(f_{T,\emptyset }) = 1 \\ \mu ^S_{s_B,r_A}(H)= \left\{ \begin{array}{l@{\quad }l} 1, &{}\text {if } r_A \in [k,1]\\ 0, &{}\text {if } r_A \in [0,k) \end{array}\right. \end{array}\right. \end{aligned}$$

(57)

We’ll show that Alice’s strategy is optimal given Bob’s belief. If Alice receives the $T$ signal, she does not report any $r_A > Y_T$ by definition of $Y_T$. She may be indifferent between reporting $Y_T$ and $f_{T,\emptyset }$. For any $r_A < Y_T$, we have $r_A < k$ and Bob’s belief sets $\mu ^S_{s_B,r_A}(H) = 0$ for any $r_A < k$. So for $r_A < Y_T$, reporting $r_A = f_{T,\emptyset }$ dominates reporting any other value. Thus, it is optimal for Alice to report $f_{T,\emptyset }$ when having the $T$ signal.

If Alice receives the $H$ signal, according to the definitions of $Y_{-H}$ and $Y_{H}$, she would only report values in $[Y_{-H}, Y_{H}]$. Given Bob’s belief, Alice would only report some $r_A \in [k, Y_H]$. Because $f_{H,\emptyset } \le k$, Alice maximizes her expected MSR payoff by reporting $r_A =k$ for any $r_A \in [k, Y_H]$. Therefore, it is optimal for Alice to report $r_A = k$ after receiving the $H$ signal.

We can show that Bob’s belief is consistent with Alice’s strategy by mechanically applying Bayes’ rule (argument omitted). Hence, for each $k \in [\max (Y_T, f_{H,\emptyset }), Y_H]$, $SE_2(k)$ is a separating PBE of our game.

Next, we assume $Y_T < f_{H,\emptyset }$ and consider that Alice reports $r_A \in [\max (Y_{-H}, Y_T), f_{H,\emptyset })$ after receiving the $H$ signal. For every $k \in [\max (Y_{-H}, Y_T), f_{H,\emptyset })$, we prove that the following pair of Alice’s strategy and Bob’s belief forms a separating PBE of our game:

$$\begin{aligned} SE_3(k): \left\{ \begin{array}{l} \sigma ^S_H(k) = 1, \sigma ^S_T(f_{T,\emptyset }) = 1 \\ \mu ^S_{s_B,r_A}(H)= \left\{ \begin{array}{l@{\quad }l} 1, &{}\text {if } r_A = k \\ 0, &{}\text {if } r_A \in [0,k) \cup (k,1] \end{array}\right. \end{array}\right. \end{aligned}$$

(58)

We’ll show that Alice’s strategy is optimal given Bob’s belief. If Alice receives the $T$ signal, she does not report any $r_A > Y_T$ by definition of $Y_T$ and is at best indifferent between reporting $Y_T$ and reporting $f_{T,\emptyset }$. For any $r_A \in [0,Y_T)$, Bob’s belief sets $\mu ^S_{s_B,r_A}(H) = 0$ since $k \ge Y_T$. For any $r_A \in [0, Y_T)$, Alice maximizes her expected market scoring rule payoff by reporting $r_A = f_{T,\emptyset }$. Thus, it is optimal for Alice to report $f_{T,\emptyset }$ when having the $T$ signal.

If Alice receives the $H$ signal, for any $r_A \in [0,1] \backslash \{k\}$, Alice maximizes her expected MSR payoff by reporting $f_{H,\emptyset }$. By definition, we know that $Y_{-H} \le k < f_{H,\emptyset }$. Given Bob’s belief

$$\begin{aligned} L(f_{H,\emptyset }, k) \le L(f_{H,\emptyset }, Y_{-H}) = E_{S_B}[Q(f_{H,S_B})-Q(f_{T,S_B}) \mid s_A] \end{aligned}$$

(59)

By switching from reporting $f_{H,\emptyset }$ to reporting $k$, Alice’s expected gain in outside payoff is greater than or equal to her loss in her expected MSR payoff. So she weakly prefers reporting $k$ to reporting $f_{H,\emptyset }$. By enforcing the consistency with Bob’s belief, Alice’s strategy must be to report $k$ after receiving the $H$ signal.

We can show that Bob’s belief is consistent with Alice’s strategy by mechanically applying Bayes’ rule (argument omitted). Hence, if $Y_T < f_{H,\emptyset }$, for each $k \in [\max (Y_{-H}, Y_T), f_{H,\emptyset })$, $SE_3(k)$ is a separating PBE of this game. $\square$

Appendix 6: Proof of Theorem 4

Proof

If $Y_{-H} \le Y_{-T}$, for every $k \in [Y_{-H}, Y_{-T}]$, we prove the following pair of Alice’s strategy and Bob’s belief forms a separating PBE of our game:

$$\begin{aligned} SE_4(k): \left\{ \begin{array}{l} \sigma ^S_H(k) = 1, \sigma ^S_T(f_{T,\emptyset }) = 1 \\ \mu ^S_{s_B,r_A}(H)= \left\{ \begin{array}{l@{\quad }l} 0, &{}\text {if } r_A \in (k,1]\\ 1, &{}\text {if } r_A \in [0,k] \end{array}\right. \end{array}\right. \end{aligned}$$

(60)

We’ll show that Alice’s strategy is optimal given Bob’s belief. If Alice receives the $T$ signal, she does not report any $r_A < Y_{-T}$ by definition of $Y_T$ and is at best indifferent between reporting $Y_{-T}$ and $f_{T,\emptyset }$. For any $r_A > Y_{-T}$, because Bob’s belief sets $\mu ^S_{s_B,r_A}(H) = 0$, reporting $f_{T,\emptyset }$ dominates reporting any other value in this range. Thus, it is optimal for Alice to report $f_{T,\emptyset }$ when having the $T$ signal.

If Alice receives the $H$ signal, for any $r_A \in (k, 1]$, Alice maximizes her expected MSR payoff by reporting $r_A = f_{H,\emptyset }$. For any $r_A \in [Y_{-H},k]$, Alice maximizes her expected MSR payoff by reporting $r_A = k$. By definition of $Y_{-H}$, Alice is better off reporting $k$ than reporting $f_{H,\emptyset }$ since

$$\begin{aligned} L(f_{H,\emptyset }, k) \le L(f_{H,\emptyset }, Y_{-H}) = E_{S_B}[Q(f_{H,S_B})-Q(f_{T,S_B}) \mid s_A] \end{aligned}$$

(61)

Therefore, it is optimal for Alice to report $k$ after receiving the $H$ signal.

We can show that Bob’s belief is consistent with Alice’s strategy by mechanically applying Bayes’ rule (argument omitted). Hence, if $Y_{-H} \le Y_{-T}$, for every $k \in [Y_{-H}, Y_{-T}]$, $SE_4(k)$ is a separating PBE. $\square$

Appendix 7: Proof of Proposition 5

Proof

The existence of a separating PBE requires $Y_H \ge Y_T$ by Theorem 2. By Lemma 2, we have $\sigma _T(f_{T,\emptyset }) = 1$ at any separating PBE.

By Theorem 3, for every $r_A \in [\max (Y_{-H}, Y_T), Y_H]$, there exists a pure strategy separating PBE in which Alice reports $r_A$ with probability $1$ after receiving the $H$ signal. Now suppose that Bob’s belief satisfies the domination-based refinement. Consider 2 cases.

• (1) Assume that $f_{H,\emptyset } > Y_T$. Then we must have $f_{H,\emptyset } \in [\max (Y_{-H}, Y_T), Y_H]$. By Lemma 5, Bob’s belief must set $\mu _{s_B,f_{H,\emptyset }}(T) = 0$. Thus, reporting $f_{H,\emptyset }$ is strictly optimal for Alice since reporting $f_{H,\emptyset }$ strictly maximizes Alice’s expected market scoring rule payoff and weakly maximizes Alice’s expected outside payoff. Therefore, there are no longer pure strategy separating PBE in which Alice reports $r_A \in [\max (Y_{-H}, Y_T), Y_H] \backslash \{f_{H,\emptyset }\}$ after receiving the $H$ signal.

• (2) Assume that $f_{H,\emptyset } \le Y_T$. Then we must have $Y_{-H} < Y_T$, and the interval $[\max (Y_{-H}, Y_T), Y_H]$ can be reduced to $[Y_T, Y_H]$. By Lemma 5, Bob’s belief must set $\mu _{s_B,r_A}(T) = 0$ for any $r_A \in (Y_T, Y_H]$. If Alice receives the $H$ signal, given Bob’s belief, Alice would not report any $r_A \in (Y_T, Y_H]$ because there always exists a $r_A' \in (Y_T, r_A)$ such that reporting $r_A'$ is strictly better than reporting $r_A$ for Alice. Therefore, there no longer exist pure strategy separating PBE in which Alice reports $r_A \in [\max (Y_{-H}, Y_T), Y_H] \backslash \{Y_T\}$ after receiving the $H$ signal.

Hence, Alice would not report $r_A \in [\max (Y_{-H}, Y_T), Y_H] \backslash \max (f_{H,\emptyset }, Y_T)$ after receiving the $H$ signal at any separating PBE satisfying the domination-based belief refinement.

By Theorem 4, if $Y_H \ge Y_T$ and $Y_{-H} \le Y_{-T}$, for every $r_A \in [Y_{-H}, Y_{-T}]$, there exists a pure strategy separating PBE in which Alice reports $r_A$ with probability $1$ after receiving the $H$ signal. By Lemma 5, Bob’s belief must set $\mu _{s_B,r_A}(T) = 0$ for any $r_A \in [Y_{-H}, Y_{-T})$. Then, if Alice receives the $H$ signal, given Bob’s belief, Alice would not report any $r_A \in [Y_{-H}, Y_{-T})$ because there always exists a $r_A' \in (r_A, Y_{-T})$ such that reporting $r_A'$ is strictly better than reporting $r_A$ for Alice.

Also, Alice would not report $Y_{-T}$ after receiving the $H$ signal for the following reasons. We consider 2 cases. If $f_{H,\emptyset } \ge Y_T$, then Alice’s MSR payoff is strictly better by reporting $f_{H,\emptyset }$ than reporting $Y_{-T}$. Otherwise, if $f_{H,\emptyset } < Y_T$, we know that $Y_{-T} < Y_T$ and hence, by Proposition 3, $L(f_{H,\emptyset } , Y_{-T}) < L(f_{H,\emptyset }, Y_T)$. Consider $r_A = Y_T + \epsilon$ for a small $\epsilon > 0$ such that $L(f_{H,\emptyset } , Y_{-T}) > L(f_{H,\emptyset }, r_A)$. Such an $\epsilon$ must exist because as $\epsilon \rightarrow 0$, $L(f_{H,\emptyset }, r_A) \rightarrow L(f_{H,\emptyset }, Y_T)$. Alice’s MSR payoff is strictly better by reporting $r_A$ than reporting $Y_{-T}$. Given Bob’s belief, we know that $\mu _{s_B,r_A}(T) = 0$ and $\mu _{s_B,Y_{-T}}(T) \ge 0$. So Alice’s outside payoff is weakly better when reporting $r_A$ than reporting $Y_{-T}$. Therefore, reporting $r_A = Y_T + \epsilon$ strictly dominates reporting $Y_{-T}$.

Hence, there are no longer pure strategy separating PBE in which Alice reports $r_A \in [Y_{-H}, Y_{-T}]$ after receiving the $H$ signal.

It remains to show that there exists a belief for Bob satisfying the refinement so that Alice’s strategy $\sigma _H(\max (f_{H,\emptyset },Y_T)) = 1, \sigma _T(f_{T,\emptyset }) = 1$ and Bob’s belief form a PBE. It is straightforward to verify that Bob’s belief in the PBE $SE_1$ described in (12) is such a belief. $\square$

Appendix 8: Proof of Proposition 7

Proof

Let $r$ be the unique value in $[0, f_{H,\emptyset }]$ satisfying $L(f_{H,\emptyset }, r) = L(f_{H,\emptyset }, Y_T)$. Consider a PBE satisfying the domination-based refinement. We will show that there exists an $\epsilon > 0$ such that if Alice receives the $H$ signal, then reporting any $r_A \le r$ is strictly worse than reporting $Y_T + \epsilon$.

By definition of $r$, we have that $L(f_{H,\emptyset }, r_A) \ge L(f_{H,\emptyset }, r) = L(f_{H,\emptyset }, Y_T), \forall r_A \le r$. We consider 2 cases.

• (1) $r_A < r$: Choose any $0 < \epsilon < r - r_A$, then we must have $L(f_{H,\emptyset }, r_A) > L(f_{H,\emptyset }, r - \epsilon ) = L(f_{H,\emptyset }, Y_T + \epsilon )$. Since the PBE satisfies the domination-based refinement, then Bob’s belief must set $\mu _{s_B,r_A}(T) = 0, \forall r_A \in (Y_T, Y_H]$. Alice’s expected outside payoff by reporting $Y_T + \epsilon$ is weakly better than her expected outside payoff by reporting $r_A$. Therefore, for any $\epsilon \in (0, r - r_A)$, Alice is strictly worse off reporting any $r_A < r$ than reporting $Y_T + \epsilon$.

• (2) $r_A = r$: For any small $\epsilon > 0$, we have that $L(f_{H,\emptyset }, r) < L(f_{H,\emptyset }, Y_T + \epsilon )$. However as $\epsilon \rightarrow 0$, $L(f_{H,\emptyset }, Y_T + \epsilon ) - L(f_{H,\emptyset }, r) \rightarrow 0$. Since $r < f_{H,\emptyset } < Y_T$, if Alice reports $r$ after receiving $H$ signal at any PBE, then Bob’s belief must set $\mu _{s_B,r}(T) > 0$. Since the PBE satisfies the domination-based refinement, then Bob’s belief must set $\mu _{s_B,Y_T + \epsilon }(T) = 0, for any\, 0 < \epsilon \le Y_H - Y_T$. Regardless of $\epsilon$, Alice’s expected outside payoff by reporting $Y_T + \epsilon$ is strictly better than her expected outside payoff by reporting $r$. However, as $\epsilon$ approaches $0$, the difference between Alice’s expected market scoring rule payoff for these two reports goes to $0$. Hence, there must exist $\epsilon > 0$ such that Alice’s total expected payoff by reporting $r$ is strictly less than her total expected payoff by reporting $Y_T + \epsilon$. $\square$

Appendix 9: Proof of Theorem 10

Proof

We will show that among all pure strategy separating PBE of our game, Bob’s expected payoff is maximized in $SE_2(Y_H)$, defined in Eq. (57).

In all separating PBE, the sum of Alice and Bob’s expected payoffs inside the market is the same. Thus, the separating PBE that maximizes Bob’s payoff is also the separating PBE that minimizes Alice’s payoff.

By Lemma 2, in any separating PBE, Alice must report $f_{T,\emptyset }$ after receiving the $T$ signal. Therefore, Alice’s expected payoff after receiving the $T$ signal is the same at any separating PBE.

For any separating PBE, Alice may report $r \in [Y_{-H}, Y_H]$ after receiving the $H$ signal. In $[Y_{-H}, Y_H]$, reporting $Y_H$ or $Y_{-H}$ maximizes Alice’s loss in her MSR payoff and thus minimizes Alice’s expected payoff after receiving the $H$ signal. Reporting $Y_H$ corresponds to the separating PBE $SE_2(Y_H)$ and reporting $Y_{-H}$ corresponds to the separating PBE $SE_4(Y_{-H})$.

If $Y_{-H} \le Y_{-T}$, the separating PBE $SE_4(Y_{-H})$ exists, by the proof of Theorem 4 in Appendix 6. We know that $Y_{-H} \le Y_{-T}$ implies $Y_H \ge Y_T$ by the proof of Theorem 2. Thus, when the separating PBE $SE_4(Y_{-H})$ exists, the separating PBE $SE_2(Y_H)$ also exists and Alice’s total expected payoff at these two separating PBE are the same.

If $Y_{-H} > Y_{-T}$, the separating PBE $SE_4(Y_{-H})$ does not exist. However, if any separating PBE exists, then we must have $Y_H \ge Y_T$, and the separating PBE $SE_2(Y_H)$ must exist.

Hence, the separating PBE $SE_2(Y_H)$ maximizes Bob’s expected payoff among all separating PBE of our game. $\square$

Appendix 10: Proof of Theorem 11

Proof

Sufficient condition

First, we show that satisfying at least one of the two pairs of inequalities is a sufficient condition for a separating PBE to exist for our game.

If inequalities (30) and (31) are satisfied, we can show that $SE_5$ is a separating PBE of our game.

$$\begin{aligned} SE_5: \left\{ \begin{array}{l} \sigma ^S_H(\max \,(Y_T,f_{H,\emptyset }) ) = 1, \sigma ^S_T(f_{T,\emptyset }) = 1\\ \mu ^S_{s_B,r_A}(H)= \left\{ \begin{array}{l@{\quad }l} 1, &{}\text {if } r_A \in [Y_T,1]\\ 0, &{}\text {if } r_A \in [0,Y_T) \end{array}\right. \end{array}\right. \end{aligned}$$

(62)

First, we show that Alice’s strategy is optimal given Bob’s belief. Since inequality (30) is satisfied, $Y_T$ is a well defined value in $[f_{T,\emptyset }, 1]$. If $f_{H,\emptyset } < Y_T$, then it is optimal for Alice to report $Y_T$ after receiving the $H$ signal because her gain in outside payoff is greater than her loss in the MSR payoff by inequality (31). Otherwise, if $f_{H,\emptyset } \ge Y_T$, then it’s optimal for Alice to report $f_{H,\emptyset }$ after receiving the $H$ signal. Therefore, Alice’s optimal strategy after receiving the $H$ signal is to report $\max \,(f_{H,\emptyset },Y_T)$. When Alice receives the $T$ signal, Alice would not report any $r_A \ge Y_T$ by definition of $Y_T$. Any other report $r_A \in [0, Y_T)$ is dominated by a report of $f_{T,\emptyset }$ given Bob’s belief. Therefore, it is optimal for Alice to report $f_{T,\emptyset }$ after receiving the $T$ signal. Moreover, we can show that Bob’s belief is consistent with Alice’s strategy by mechanically applying Bayes’ rule (argument omitted). Given the above arguments, $SE_5$ is a separating PBE of this game.

Similarly, if inequalities (32) and (33) are satisfied, then we can show that $SE_6$ is a separating PBE of our game.

$$\begin{aligned} SE_6: \left\{ \begin{array}{l} \sigma ^S_H(Y_{-T}) = 1, \sigma ^S_T(f_{T,\emptyset }) = 1 \\ \mu ^S_{s_B,r_A}(H)= \left\{ \begin{array}{l@{\quad }l} 0, &{}\text {if } r_A \in (Y_{-T},1]\\ 1, &{}\text {if } r_A \in [0,Y_{-T}] \end{array}\right. \end{array}\right. \end{aligned}$$

(63)

First, we show that Alice’s strategy is optimal given Bob’s belief. Since inequality (32) is satisfied, $Y_{-T}$ is well defined. If Alice receives the $H$ signal, reporting any $r_A \in [0,Y_{-T}]$ gives her higher outside payoff than reporting any $r_A \in (Y_{-T},1]$. For any $r_A \in [0,Y_{-T}]$, her outside payoff is fixed and reporting $r_A = Y_{-T}$ maximizes her market scoring rule payoff. Therefore, it is optimal for Alice to report $r_A = Y_{-T}$ after receiving the $H$ signal. If Alice receives the $T$ signal, she does not report any $r_A < Y_{-T}$ by definition of $Y_{-T}$. Given Bob’s belief, she is indifferent between reporting $Y_{-T}$ and $f_{T,\emptyset }$. For any $r_A > Y_{-T}$, Bob’s belief sets $\mu ^S_{s_B,r_A}(H) = 0$, so it is optimal for Alice to report $f_{T,\emptyset }$ to maximize her MSR payoff. We can show that Bob’s belief is consistent with Alice’s strategy by mechanically applying Bayes’ rule (argument omitted). Hence, $SE_6$ is a separating PBE of our game.

Necessary condition

Second, we show that, if there exists a separating PBE of our game, then at least one of the two pairs of inequalities must be satisfied. We prove this by contradiction. Suppose that there exists a separating PBE of our game but at least one of the two inequalities in each of the two pairs of inequalities is violated.

Suppose that at least one of the inequalities (30) and (31) is violated. Then, we can show that Alice does not report any value $r_A \in [f_{T,\emptyset },1]$ after receiving the $H$ signal at any separating PBE. We divide the argument for this into 2 cases.

• (1) If inequality (30) is violated, we know that $Y_T$ is not well defined. We show by contradiction that Alice does not report any value in $[f_{T,\emptyset },1]$ after receiving the $H$ signal. Suppose that at a separating PBE, Alice reports $r_A \in [f_{T,\emptyset },1]$ with positive probability after receiving the $H$ signal. Since this PBE is separating, Bob’s belief must be that $\mu _{s_B,r_A}(H) = 1$ to be consistent with Alice’s strategy. By Lemma 2, in any separating PBE, Bob’s belief must be $\mu _{s_B,f_{T,\emptyset }}(H) = 0$ and Alice must report $f_{T,\emptyset }$ after receiving the $T$ signal. Since inequality (30) is violated, then we have that

  $$\begin{aligned} L_m(f_{T,\emptyset },r_A) \le L_m(f_{T,\emptyset },1) < E_{S_B}[Q(f_{H,S_B})-Q(f_{T,S_B}) \mid S_A = T], \end{aligned}$$

  (64)

  so Alice would strictly prefer to report $r_A$ rather than $f_{T,\emptyset }$ after receiving the $T$ signal, which is a contradiction.

• (2) Otherwise, if inequality (30) is satisfied but inequality (31) is violated, then we know that $Y_T$ is well defined. If $f_{H,\emptyset } \ge Y_T$, then inequality (31) is automatically satisfied, so we must have that $f_{H,\emptyset } < Y_T$ and $L_m(f_{H,\emptyset },Y_T) > E_{S_B}[Q(f_{H,S_B})-Q(f_{T,S_B}) \mid S_A = H]$. Then Alice does not report any $r_A \in [Y_T, 1]$ after receiving the $H$ signal because doing so is dominated by reporting $f_{H,\emptyset }$. Next, we can show by contradiction that Alice does not report any $r_A \in [f_{T,\emptyset }, Y_T)$ after receiving the $H$ signal at any separating PBE. Suppose that at any separating PBE, Alice reports $r_A \in [f_{T,\emptyset }, Y_T)$ with positive probability after receiving the $H$ signal. Since this PBE is separating, Bob’s belief must be that $\mu _{s_B,r_A}(H) = 1$ to be consistent with Alice’s strategy. By Lemma 2, in any separating PBE, Alice must report $f_{T,\emptyset }$ after receiving the $T$ signal and Bob’s belief must be $\mu _{s_B,f_{T,\emptyset }}(H) = 0$. Thus, for $r_A \in (Y_{-T}, Y_T)$, by definitions of $Y_T$ and $Y_{-T}$, Alice would strictly prefer to report $r_A$ rather than $f_{T,\emptyset }$ after receiving the $T$ signal, which is a contradiction.

Hence, if at least one of the inequalities (30) and (31) is violated, then at any separating PBE, Alice does not report any $r_A \in [f_{T,\emptyset },1]$ after receiving the $H$ signal.

Similarly, we can show that, if at least one of the inequalities (32) and (33) is violated, Alice does not report any value $r_A \in [0, f_{T,\emptyset }]$ after receiving the $H$ signal at any separating PBE. We again consider 2 cases:

• (1) If inequality (32) is violated, we know that $Y_{-T}$ is not well defined. Then we can show that Alice does not report any value in $[0, f_{T,\emptyset }]$ after receiving the $H$ signal. We prove by contradiction. Suppose that at a separating PBE, Alice reports $r_A \in [0, f_{T,\emptyset }]$ with positive probability after receiving the $H$ signal. Since this PBE is separating, Bob’s belief must be that $\mu _{s_B,r_A}(H) = 1$ to be consistent with Alice’s strategy. By Lemma 2, in any separating PBE, Bob’s belief must be $\mu _{s_B,f_{T,\emptyset }}(H) = 0$ and Alice must report $f_{T,\emptyset }$ after receiving the $T$ signal. Since inequality (32) is violated, we have that

  $$\begin{aligned} L_m(f_{T,\emptyset },r_A) \le L_m(f_{T,\emptyset },\emptyset ) < E_{S_B}[Q(f_{H,S_B})-Q(f_{T,S_B}) \mid S_A = T], \end{aligned}$$

  (65)

  so Alice would strictly prefer to report $r_A$ rather than $f_{T,\emptyset }$ after receiving the $T$ signal, which is a contradiction.

• (2) Otherwise, if inequality (32) is satisfied but inequality (33) is violated, then we know that $Y_{-T}$ is well defined. Also, we must have that $L_m(f_{H,\emptyset },Y_{-T}) > E_{S_B}[Q(f_{H,S_B})-Q(f_{T,S_B}) \mid S_A = H]$. Then Alice does not report any $r_A \in [0, Y_{-T}]$ after receiving the $H$ signal because doing so is dominated by reporting $f_{H,\emptyset }$. Next, We can show by contradiction that at any separating PBE, Alice does not report any $r_A \in (Y_{-T}, f_{T,\emptyset }]$ after receiving the $H$ signal. Suppose that at any separating PBE, Alice reports $r_A \in (Y_{-T}, f_{T,\emptyset }]$ with positive probability after receiving the $H$ signal. Since this PBE is separating, Bob’s belief must be that $\mu _{s_B,r_A}(H) = 1$ to be consistent with Alice’s strategy. By Lemma 2, in any separating PBE, Alice must report $f_{T,\emptyset }$ after receiving the $T$ signal and Bob’s belief must be $\mu _{s_B,f_{T,\emptyset }}(H) = 0$. Thus, for $r_A \in (Y_{-T}, Y_T)$, by definitions of $Y_T$ and $Y_{-T}$, Alice would strictly prefer to report $r_A$ rather than $f_{T,\emptyset }$ after receiving the $T$ signal, which is a contradiction.

Hence, if at least one of the inequalities (32) and (33) is violated, in any separating PBE, Alice does not report any $r_A \in [0, f_{T,\emptyset }]$ after receiving the $H$ signal.

Therefore, if at least one of the two inequalities in the two pairs of inequalities is violated, then at any separating PBE, Alice does not report any $r_A \in [0,1]$ after receiving the $H$ signal. This contradicts our assumption that a separating PBE exists for our game. $\square$