Abstract
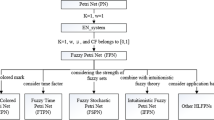
Fuzzy Petri net (FPN) provides an extremely competent basis for the implementation of computing reasoning processes and the modeling of systems with uncertainty. This paper reviews recent developments of the FPN and its industrial applications. Several important aspects of FPN’s background, history and formalisms are discussed, including the reasoning algorithm and relevant industrial applications; after which we present our conclusions and suggestions for future research.












Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Abdulkareem AA, Abaas AH, Radi AT (2011) Transmission line protection based on neural network, fuzzy neural and fuzzy neural Petri net. Aust J Basic Appl Sci 5(11):1466–1479
Amin M, Shebl D (2014) Reasoning dynamic fuzzy systems based on adaptive fuzzy higher order Petri nets. Inf Sci 286:161–172
An R, Liang W (2013) Unobservable fuzzy Petri net diagnosis technique. Aircr Eng Aerosp Techno 85(3):215–221
Asthana R, Ahuja NJ, Darbari M (2011) Model proving of urban traffic control using neuro Petri nets and fuzzy logic. Int Rev Comput Softw 6(6):983–987
Aura T, Lilius J (2000) A causal semantics for time Petri nets. Theor Comput Sci 243(1):409–447
Barzegar S, Davoudpour M, Meybodi MR, Sadeghian A, Tirandazian M (2011) Formalized learning automata with adaptive fuzzy coloured Petri net; an application specific to managing traffic signals. Sci Iran 18(3):554–565
Brauer W, Reisig W (2006) Carl Adam Petri and “Petri Nets”, Translation from Informatik- Spektrum, vol. 29. Springer, Berlin, pp 369–374
Bugarin AJ, Barro S (1994a) Fuzzy reasoning supported by Petri nets. IEEE Trans Fuzzy Syst 2(2):135–150
Bugarin AJ, Barro S (1994b) Goal-driven reasoning for fuzzy Knowledge-based systems using a petri net formalism. In: Proceedings of the third IEEE conference on fuzzy systems 1994. IEEE world congress on computational intelligence, pp 2061–2066
Bugarin A, Carinena P, Delgado MF, Barro S (1996) Petri net representation of fuzzy reasoning under incomplete information. In: Proceedings of the 26th IEEE international symposium on multiple-valued logic 1996, pp 172–177
Cao Y, Chen G (2010) A fuzzy petri-nets model for computing with words. IEEE Trans Fuzzy Syst 18(3):486–499
Cardoso J (1999) Fuzziness in Petri nets. In: Camargo H (ed) Studies in fuzziness and soft computing, vol 22. Springer, Heidelberg
Chen SM, Ke JS, Chang JF (1990) Knowledge representation using fuzzy Petri nets. IEEE Trans Knowl Data Eng 2(3):311–319
Chen SM (2000) Fuzzy backward reasoning using fuzzy Petri nets. IEEE Trans Syst Man Cybern B Cybern 30(6):846–856
Chen SM (2002) Weighted fuzzy reasoning using weighted fuzzy Petri nets. IEEE Trans Knowl Data Eng 14(2):386–397
Chen WL, Kan CD, Lin CH, Chen T (2014) A rule-based decision-making diagnosis system to evaluate arteriovenous shunt stenosis for hemodialysis treatment of patients using fuzzy petri nets. IEEE J Biomed Health Inform 18(2):703–713
Cheng YH, Yang LA (2009) A fuzzy Petri nets approach for railway traffic control in case of abnormality: evidence from Taiwan railway system. Expert Syst Appl 36(4):8040–8048
Chun MG, Bien ZN (1993) Fuzzy Petri-net representation and reasoning methods for rule-based decision-marking system. IEICE Trans Fundam Electron Commun Sci E76A(6):974–983
Co JH, Swami A, Chen IR (2012) Modeling and analysis of trust management with trust chain optimization in mobile ad hoc networks. J Netw Comput Appl 35(3):1001–1012
Fenton NE, Neil M, Galan Caballero J (2007) A generalized associative Petri net for reasoning. IEEE Trans Knowl Data Eng 19(9):1241–1251
Gao MM, Wu ZM, Zhou MC (2000) Petri net-based formal reasoning algorithm for fuzzy production rule-based systems. In: Proceedings of 2000 IEEE international conference on systems, man, and cybernetics, Vol. 4, pp 3093–3097
Gao MM, Zhou MC, Tang Y (2004) Intelligent decision making in disassembly process based on fuzzy reasoning Petri nets Systems. IEEE Trans Man Cybernet B Cybernet 34(5):2029–2034
Gao MM, Zhou MC, Huang XG, Wu ZM (2003) Fuzzy reasoning Petri nets. IEEE Trans Syst Man Cybernet A Syst Hum 33(3):314–324
Garg K (1987) An approach to performance specification of communication protocols using timed Petri nets. IEEE Trans Softw Eng SE–13(12):1297–1310
Garg ML, Ahson SI, Gupta PV (1991) A fuzzy Petri net for knowledge representation and reasoning. Inf Proces Lett 39(3):165–171
Gniewek L, Kluska J (2004) Hardware implementation of fuzzy Petri net as a controller. IEEE Trans Syst Man Cybern B Cybern 34(3):1315–1324
Gniewek L (2013) Sequential control algorithm in the form of fuzzy interpreted Petri net. IEEE Trans Syst Man Cybern Syst 43(2):451–459
Gong FT, Wang JY (2012) Research of weighted fuzzy fault diagnosis based on adaptive neural network. Int J Digital Content Technol Appl 6(9):118–124
Gua T, Bahri PA (2002) A survey of Petri net applications in batch processes. Comput Ind 47(1):99–111
Guan YF, Kezunovic M (2013) Contingency-based nodal market operation using intelligent economic alarm processor. IEEE Trans Smart Grid 4(1):540–548
Ha S, Suh HWA (2008) Timed colored Petri nets modeling for dynamic workflow in product development process. Comput Ind 59(2–3):193–209
Ha MH, Li Y, Li HJ, Wang P (2005) A new form of Knowledge representation and reasoning. In: Proceedings of 2005 international conference on machine learning and cybernetics, Vol. 4, pp 2577–2582
Ha MH, Li Y, Wang XF (2007) Fuzzy knowledge representation and reasoning using a generalized fuzzy petri net and a similarity measure. Soft Comput 11(4):323–327
He ZY, Yang JW, Zeng QF, Zang TL (2014) Fault section estimation for power systems based on adaptive fuzzy Petri nets. Int J Comput Intell Syst 7(4):605–614
Heng PA, Wong TT, Yang R, Chui YP, Xie YM, Leung KS, Leung P (2006) Intelligent inferencing and haptic simulation for Chinese acupuncture learning and training. IEEE Trans Inf Technol Biomed 10(1):28–41
Holt AW, Commoner F, Euents Conditioii (1970) Applied data research. ACM, New York; also in records: project MAC Conference on concurrent systems and parallel computation. ACM, New York, pp 1–52
Hu C, Li P, Wang H (2003) Improved modeling algorithm of fuzzy petri net for fuzzy reasoning. In: Proceedings of IEEE international conference on systems, man and cybernetics, pp 4992–4997
Hu H, Li Z, Al-Ahmari A (2011) Reversed fuzzy Petri nets and their application for fault diagnosis. Comput Ind Eng 60(4):505–510
Hugo C, Pedro L (2012) Robot task plan representation by Petri nets: modeling, identification, analysis and execution. Auton Robots 33(4):337–360
Jensen K (1981) Coloured Petri nets and the invariant-method. Theor Comput Sci 14:317–336
Jensen K (1983) High-level Petri nets. Springer, Berlin
Jensen K (1987) Colored Petri nets. Lecture Notes in Computer Science, pp 254, 248–299
Jensen K (1992) Coloured Petri nets. Basic concept, analysis methods and practical use, vol 1. Springer, Berlin
Jensen K (1995) Coloured Petri nets: basic concept, analysis methods and practical use, vol 2. Springer, Berlin
Jensen K (1997) Coloured Petri nets: basic concept, analysis methods and practical use, vol 3. Springer, Berlin
Jensen K, Kristensen LM (2009) Coloured Petri nets: modelling and validation of concurrent systems. Springer, Berlin
Jung CH, Lee TE (2012) An efficient mixed integer programming model based on timed Petri nets for diverse complex cluster tool scheduling problems. IEEE Trans Semicond Manuf 25(2):186–199
Khan SA, Zafar NA, Ahmad F (2011) Petri net modeling of railway crossing system using fuzzy brakes. Int J Phys Sci 6(14):3389–3397
Konar A, Chakraborty UK, Wang PP (2005) Supervised learning on a fuzzy Petri net. Inf Sci 172(3–4):397–416
Konar A, Jain L (2005) Cognitive engineering: a distributed approach to machine intelligence. Springer, London
Kumar N, Borm JH, Kumar A (2012) Reliability analysis of waste clean-up manipulator using genetic algorithms and fuzzy methodology. Comput Oper Res 39(2):310–319
Lee SJ, Seong PH (2004) Development of automated operating procedure system using fuzzy colored petri nets for nuclear power plants. Ann Nuclear Energy 31(8):849–869
Lee GB, Zandong H, Lee JS (2004) Automatic generation of ladder diagram with control Petri net. J Intell Manuf 15(2):245–252
Lee CK, Lin CL, Shiu BM (2009) Autonomous vehicle parking using hybrid artificial intelligent approach. J Intell Robot Syst Theory Appl 56(3):319–343
Lee CH, Lee YC (2012) Nonlinear systems design by a novel fuzzy neural system via hybridization of electromagnetism-like mechanism and particle swarm optimization algorithms. Inf Sci 186(1):59–72
Li XO, Lara-Rosano F (1999) Weighted Fuzzy Petri net model for Knowledge learning and reasoning. In: Proceedings of international joint conference on neural networks, IJCNN’99, Vol. 4, pp 2368–2372
Li XO, Yu W, Lara-Rosano F (2000) Dynamic knowledge inference and learning under adaptive fuzzy Petri net framework. IEEE Trans Syst Man Cybern C Appl Rev 30(4):442–450
Lipp HP (1984) Application of a fuzzy Petri net for controlling complex industrial processes. In : Proceedings of IFAC Conference on fuzzy information control, pp 471–477
Liu D, Wang J, Chan SC, Sun J, Zhang L (2002) Modeling workflow processes with colored Petri nets. Comput Ind 49(3):267–281
Liu J, Wang W, Xiao Q, Yang Z (2010) Fault diagnosis for flight control system of unmanned aerial vehicle using fuzzy petri nets. ICIC Exp Lett 4(4):1319–1324
Liu J, Chen K, Wang Z (2011a) Fault analysis for flight control system using weighted fuzzy Petri Nets. J Converg Inf Technol 6(3):46–155
Liu Z, Li H, Zhou P (2011b) Towards timed fuzzy Petri net algorithms for chemical abnormality monitoring. Exp Syst Appl 38(8):9724–9728
Liu HC, Liu L, Lin QL, Liu N (2013a) Knowledge acquisition and representation using fuzzy evidential reasoning and dynamic adaptive fuzzy Petri nets. IEEE Trans Cybern 43(3):1059–1072
Liu HC (2013b) Dynamic adaptive fuzzy Petri nets for knowledge representation and reasoning. IEEE Trans Syst Man Cybern Syst 46(3):1399–1410
Liu HC, Lin QL, Ren ML (2013c) Fault diagnosis and cause analysis using fuzzy evidential reasoning approach and dynamic adaptive fuzzy Petri nets. Comput Ind Eng 66(4):899–908
Looney CG (1988) Fuzzy Petri nets for rule-based decision making. IEEE Trans Syst Man Cybern 18(1):178–183
Luo X, Kezunovic M (2008) Implementing fuzzy reasoning Petri-nets for fault section estimation. IEEE Trans Power Delivery 23(2):676–685
Molloy MK (1982) Performance analysis using stochastic Petri nets. IEEE Trans Comput C–31(9):913–917
Murata T (1989) Petri nets: properties, analysis and applications. IEEE Proc 77:540–541
Manoj T, Leena J, Soney R (1998) Knowledge representation using fuzzy Petri nets: revisited. IEEE Trans Knowl Data Eng 10(4):666–667
Ouchi E, Tazaki Y (1997) Learning and reasoning method using fuzzy colored Petri nets under uncertainty. In: IEEE international conference on proceedings of systems, man, and cybernetics, computational cybernetics and simulation, Vol. 4, pp 3867–3871
Pamuk N, Uyaroglu Y (2012) The fault diagnosis for power system using fuzzy Petri nets. Przeglad Elektrotechniczny 88(7A):99–102
Pan HL, Jiang WR, He HH (2012) The fault diagnosis model of flexible manufacturing system workflow based on adaptive weighted fuzzy Petri net. Adv Sci Lett 11(1):811–814
Pantelopoulos A, Bourbakis NG (2010) Prognosis-a wearable health-monitoring system for people at risk: methodology and modeling. IEEE Trans Inf Technol Biomed 14(3):613–621
Parhi DR, Mohanta JC (2011) Navigational control of several mobile robotic agents using Petri-potential-fuzzy hybrid controller. Appl Soft Comput J 11(4):3546–3557
Pedrycz W, Camargo H (2003) Fuzzy timed Petri nets. Fuzzy Sets Syst 140:301–330
Peters G, Tagg R (2009) Intelligent concepts for the management of information in workflow systems. Int J Comput Intell Syst 2(4):332–342
Petri CA (1962) Kommunikation mit Automaten. Schnften des Rheinish-Wehtfalischen Institutes Cur Instrumentelle Mathematik an der Univcrstit Bonn, Heft 2, Bonn, W. Germany
Pla A, Gay P, Meléndez J, López B (2014) Petri net-based process monitoring: a workflow management system for process modeling and monitoring. J Intell Manuf 25(3):539–554
Plunnecke H, Reisig W (1991) Bibliography of Petri nets 1990. Advances in Petri Nets 1991, Lecture Notes in Computer Science, Springer, Berlin, vol. 524, pp 317–575
Pouyan AA, Shandiz HT, Arastehfar S (2011) Synthesis a Petri net based control model for a FMS cell. Comput Ind 62(5):501–508
Qiao F, Wu Q, Li L, Wang Z, Shi B (2011) A fuzzy Petri net-based reasoning method for rescheduling. Trans Inst Meas Control 33(3–4):435–455
Rajpurohit VS, Pai MMM (2012) Efficient object motion prediction using fuzzy Petri net based modeling in a robot navigational environment. Int J Veh Auton Syst 10(1–2):19–40
Ramchandani C (1974) Analysis of asynchronous concurrent systems by timed Petri nets. Massachusetts Institute of Technology, Cambridge
Ribarik S, Basic BD, Pavesic N (1999) A model for fuzzy temporal knowledge representation and reasoning. In: Fuzzy systems conference proceedings, 1999, Vol. 1, pp 216–221
Scarpelli H, Gomide F (1994) A high level net approach for discovering potential inconsistencies in fuzzy knowledge bases. Fuzzy Sets Syst 64(2):175–193
Scarpelli H, Gomide F, Yager RR (1996) A reasoning algorithm for high-level fuzzy Petri nets. IEEE Trans Fuzzy Syst 4(3):282–294
Sharma RK, Kumar D, Kumar P (2008) Predicting uncertain behavior of industrial system using FM-A practical case. Appl Soft Comput 8(1):96–109
Sharma SP, Sukavanam N, Kumar N, Kumar A (2010) Reliability analysis of complex robotic system using Petri nets and fuzzy lambda-tau methodology. Eng Comput 27(3):354–364
Sharma SP, Kumar D, Kumar A (2012) Reliability analysis of complex multi-robotic system using GA and fuzzy methodology. Appl Soft Comput J 2(1):405–415
Shen VRL (2003) Reinforcement learning for high-level fuzzy Petri nets. IEEE Trans Syst Man Cybern B Cybern 33(2):351–362
Shen VRL (2006) Knowledge representation using high-level fuzzy Petri nets. IEEE Trans Syst Man Cybern A Syst Hum 36(6):1220–1227
Shen VRL, Chang YS, Juang TTY (2010) Supervised and unsupervised learning by using petri nets. IEEE Trans Syst Man Cybern A Syst Hum 40(2):363–375
Shen VRL, Yang CY, Wang YY, Lin YH (2012) Application of high-level fuzzy Petri nets to educational grading system. Exp Syst Appl 39(17):12935–12946
Shen XY, Lei YJ, Li CH (2009). Intuitionistic fuzzy petri nets model and reasoning algorithm. In: Proceedings of the 6th international conference on fuzzy systems and knowledge discovery, pp 119–122
Shi ZF (2012) Intelligent target fusion recognition based on fuzzy Petri nets. Inf Technol J 11(4):500–550
Shih DH, Chiang HS, Lin B (2007) A generalized associative Petri net for reasoning. IEEE Trans Knowl Data Eng 19(9):1241–1251
Shih DH, Chiang HS, Lin B, Lin SB (2010) An embedded mobile ECG reasoning system for elderly patients. IEEE Trans Inf Technol Biomed 14(3):854–865
Shojafar M, Pooranian Z, Meybodi MR, Singhal M (2013) ALATO: an efficient intelligent algorithm for time optimization in an economic grid based on adaptive stochastic Petri net. J Intell Manuf 26(4):641–658
Silva M (2013) Half a century after Carl Adam Petri’s Ph.D thesis: a perspective on the field. Ann Rev Control 37:191–219
Srinivasan P, Gracanin D (1993) Approximate reasoning with Fuzzy Petri Nets. In: Proceedings of the second IEEE international conference on fuzzy systems, pp 396–401
Sun J, Qin SY, Song YH (2004) Fault diagnosis of electric power systems based on fuzzy Petri nets. IEEE Trans Power Syst 19(4):2053–2059
Tang Y, Zhou MC, Gao MM (2006) Fuzzy-Petri-net-based disassembly planning considering human factors. IEEE Trans Syst Man Cybern A Syst Hum 36(4):718–726
Tang Y (2009) Learning-based disassembly process planner for uncertainty management. Systems. IEEE Trans Syst Man Cybern A Syst Hum 39(1):134–143
Thiagarajan PS (1987) Elementary net systems. Petri nets: central models and their properties. Springer, Berlin, pp 26–59
Tiehua C, Sanderson CA (1993) Fuzzy Petri net approach to reasoning about uncertainty in robotic systems. In: Proceedings of the 1993 IEEE international conference on robotics and automation, pp 317–322
Ting Y, Lu WB, Chen CH, Wang GK (2008) A fuzzy reasoning design for fault detection and diagnosis of a computer-controlled system. Eng Appl Artif Intell 21(2):157–170
Tont G, Vladareanu L, Munteanu MS, Tont DG (2010) Markov approach of adaptive task assignment for robotic system in non-stationary environments. WSEAS Trans Syst 9(3):273–282
Tsang ECC, Yeung DS, John WTL (1999) Learning capability in fuzzy Petri nets. In: IEEE SMC’99 proceedings on the international conference on systems, man, and cybernetics, Vol. 3, pp 355–360
Tuysuz F, Kahraman C (2010) Modeling a flexible manufacturing cell using stochastic Petri nets with fuzzy parameters. Expert Syst Appl 37(5):3910–3920
Urawski R, Zhou MC (1994) Petri nets and industrial application-a tutorial. IEEE Trans Ind Electron 41(6):67–583
Van der Aalst WMP (1994) Putting high-level Petri nets to work in industry. Comput Ind 25(1):45–54
Van der Aalst WMP, van Hee KM (1996) Business process redesign: a Petri-net-based approach. Comput Ind 29(1–2):15–26
Wai RJ, Liu CM (2009) Design of dynamic petri recurrent fuzzy neural network and its application to path-tracking control of non-holonomic mobile robot. IEEE Trans Ind Electron 56(7):2667–2683
Wai RJ, Liu CM, Lin YW (2010) Robust path tracking control of mobile robot via dynamic petri recurrent fuzzy neural network. Soft Comput 15(4):743–767
Wang SL, Wu YH (1999) Reasoning in fuzzy production systems when input information is incomplete. In: FUZZ-IEEE’99 fuzzy systems conference proceedings, Vol. 3, pp 1557–1561
Wang HQ, Jiang CJ, Liao SY (2001) Concurrent reasoning of fuzzy logical Petri nets based on multi-task schedule. IEEE Trans Fuzzy Syst 9(3):444–449
Wang XZ, Xu Y, Zhu RX (2005) Multilevel weighted fuzzy reasoning with interaction. In: Proceedings of 2005 IEEE international conference on systems, man and Cybernetics, Vol. 1, pp 708–715
Wang J, Zhao N, Du W, Zhao Y, Qian Y, Jiang Z (2012) Using fuzzy clustering method to classify the component in the process of software evolution. J Inf Technol 11(3):396–398
Wang J, Shi P, Peng H, Perez-Jimenez MJ, Wang T (2013) Weighted fuzzy spiking neural P systems. IEEE Trans Fuzzy Syst 21(2):209–220
Wang S, Wu W, Yang J (2015) Deadlock prevention policy for a class of petri nets based on complementary places and elementary siphons. J Intelli Manuf 26(2):321–330
Wu Z, Hsieh SJ (2012) A real time fuzzy Petri net diagnoser for detecting progressive faults in PLC based discrete manufacturing system. Int J Adv Manuf Technol 61(1–4):405–421
Wu J, Yan S, Xie L, Gao P (2012) Reliability apportionment approach for spacecraft solar array using fuzzy reasoning Petri net and fuzzy comprehensive evaluation. Acta Astronaut 76:136–144
Wu J, Yan S, Xie L (2011) Reliability analysis method of a solar array by using fault tree analysis and fuzzy reasoning Petri net. Acta Astron 69(11–12):960–968
Xu Y (2009) A multilevel weighted reasoning algorithm using interactive weighted petri nets. In: Proceedings of 2009 international conference on machine learning and cybernetics, Vol. 1, pp 509–514
Xu QL, Zhou F, Jiao JX (2011) Affective-cognitive modeling for user experience with modular colored fuzzy petri nets. J Comput Inf Sci Eng 11(1):1–10
Yang R, Leung WS, Heng PA, Leung KS (2002) Improved algorithm on rule-based reasoning systems modeled by fuzzy Petri nets. In: Proceedings of the 2002 IEEE international conference on fuzzy systems FUZZ-IEEE’02, Vol. 2, pp 1204–1209)
Ye Y, Jiang Z, Diao X, Du G (2011) Extended event-condition-action rules and fuzzy Petri nets based exception handling for workflow management. Exp Syst Appl 38(9):10847–10861
Yeung DS, Tsang ECC (1994) Fuzzy Knowledge representation and reasoning using Petri nets. Exp Syst Appl 7(2):81–289
Yeung DS, Liu JN, Shiu SC, Fung GS (1996) Fuzzy coloured Petri nets in modelling flexible manufacturing systems. In: Proceedings of ISAI/IFIS 1996, Mexico-USA Collaboration in Intelligent Systems Technologies, pp 100-107
Yeung DS, Tsang ECC (1998) A multilevel weighted fuzzy reasoning algorithm for expert systems. IEEE Trans Syst Man Cybern A Syst Hum 28(2):149–158
Yu SK (1995) Knowledge representation and reasoning using fuzzy Pr/T net-systems. Fuzzy Sets Syst 75(1):33–45
Yu Z, Fu X, Cai Y, Vuran MC (2011) A reliable energy-efficient multi-level routing algorithm for wireless sensor networks using Fuzzy Petri Nets. Sensors 11(3):3381–3400
Yuan JM, Hou CZ, Wang XY, Wu Q (2007) Availability fuzzy evaluation based on stochastic Petri net for repairable system. Comput Eng 33(8):17–19
Yuan J, Shi HB, Liu C (2008) Backward concurrent reasoning based on fuzzy petri nets. In: IEEE world congress on computational intelligence fuzzy systems on FUZZ-IEEE 2008, pp 832–837
Yuan J, Liu C, Jiang B, Shan Y, Shang W (2010) A forward concurrent reasoning approach for rule-based systems using fuzzy colored Petri nets. In: World congress on intelligent control and automation, pp 1579–1584
Yuan Y (2009) Learning algorithm with fuzzy petri nets model based on taboo search. In: Proceedings of international conference on information engineering and computer science, pp 1–4
Zhang LL, Jiao JR (2009) Modeling production configuration using nested colored object-oriented Petri-nets with changeable structures. J Intell Manuf 20(4):359–378
Zhang B, Cui S (2008) A parallel backward reasoning study using fuzzy petri net. In: Proceedings of 2008 international conference on computer science and software engineering, pp 315–319
Zhang Y, Xu K, Yu J (2011) Modeling and optimization of hull erection process. Int J Prod Res 49(13):4157–4174
Zhao SE, Li YL, Fu R, Yuan W (2014) Fuzzy reasoning Petri nets and its application to disassembly sequence decision-making for the end-of-life product recycling and remanufacturing. Int J Comput Integr Manuf 27(5):415–421
Zhong YB (2008) The design of a controller in Fuzzy Petri net. Fuzzy Optim Decis Making 7(4):399–408
Zhou Y, Wu SL (1996) NNF and NNPrF-fuzzy petri nets based on neural network for knowledge representation, reasoning and learning. J Comput Sci Technol 11(2):133–149
Zhou F, Jiao R, Xu Q, Takahashi K (2012) User experience modeling and simulation for product ecosystem design based on fuzzy reasoning Petri nets. IEEE Trans Syst Man Cybern A Syst Hum 42(1):201–212
Acknowledgments
The authors greatly acknowledge comments from reviewers and extend heartfel gratitude to the Soft Computing Research Group (SCRP), Research Management Centre (RMC), UTM and Ministry of Higher Education Malaysia (MOHE) for Financial support through the Fundamental Research Grant Scheme (FRGS), No. R.J13000.7828.4F721.
Author information
Authors and Affiliations
Corresponding author
Appendix 1: formal definitions of FPN (2000 to 2013)
Appendix 1: formal definitions of FPN (2000 to 2013)
Formalism | Highlight |
|---|---|
\(\textit{FPN}=(P,T,D,I,O,f,\alpha ,\beta )\) (Chen 2000; Sun et al. 2004; Shih et al. 2010) | (P,T,D,I,O) is the basic net structure of FPN; \((\alpha ,\beta )\)describes correspondence between KBS and FPN |
\(\textit{AFPN}=(P,T,D,I,O,\alpha ,\beta ,Th,W)\) (Li et al. 2000) | Weight and threshold considered and added to formalism |
\(\textit{FPN}=(P,T,F,M_0 ,D,H,\alpha ,\theta ,\lambda )\) (Wang et al. 2001) | Transitions classified into five types: \(t^{1},^{and}t,^{or}t,^{and},t^{or};\) to control scale of FPN and simplify analysis |
\(\textit{WFPN}=(P,T,D,I,O,f,\alpha ,\beta ,W)\) (Chen 2002) | Chen considered the function of weight in his research and enhanced the proposed formalism |
\(\textit{HLFPN}=(P,T,F,C,V,\alpha ,\beta ,\delta )\) (Shen 2003, 2006; Shih et al. 2010) | This formalism extended the description range for FPN |
\(\textit{FRPN}=(P,R,I,O,H,\theta ,\gamma ,C)\) (Gao et al. 2003, 2004; Luo and Kezunovic 2008; Zhou et al. 2012; Guan and Kezunovic 2013) | This formalism used an algebraic form to explore parallel operation ability and used I, O, H to define relevance matrices |
\(\textit{FPN}=(P,R,D,G,R,\Delta ,\Gamma ,\Theta ,M_0 )\) (Gniewek and Kluska 2004) | This formalism focused on one-to-one correspondence between KBS and FPN |
\(\textit{FAPN}=(P,T,I,O,M,\tau ,\alpha ,\lambda )\) (Tang et al. 2006) | This formalism was based on the disassembly issue; human factors were considered. For example, places divided into two modules, one for operators, another for product subassembly or component |
\(\textit{IFPN}=(P,T,D,I,O,\mu ,f,w,H,\beta )\) (Heng et al. 2006) | This formalism considered parameters and correspondence between KBS and FPN. Moreover, dynamic certainty given and marked by f |
\(\textit{APN}=(P,T,S,D,\Lambda ,\Gamma ,I,O,C,\alpha ,\beta ,W,Th)\) (Shih et al. 2007) | This formalism derived from FPN. Compared with above, a special element, ’square’, was added in the APN model |
\(\textit{FPN}=(P,T,I,O,M,\theta ,\alpha ,\delta ,\tau ,\lambda )\) (Tang 2009) | This formalism also focused on the disassembly issue. Compared with the 8-tuple of FPN by Gao et al. (2004), this formalism used 10-tuple to describe the FPN |
\(\textit{FPN}=(P,T,I,O,\alpha ,\beta ,M_0 )\) (Cao and Chen 2010) | This formalism focused on computing with words, weight value of one for every situation |
\(\textit{FIPN}=(P,T,\Omega ,\Psi ,R,\Delta ,K,W,\Gamma ,\Theta ,M_0 ,e)\) (Gniewek 2013) | This formalism proposed a strategy to settle conflict. For instance, places were summarized in two modules, one associated with modeling a processes, another associated with modeling resources |
\(\hbox {WFSN P system}=(O,N_p ,N_r ,syn,IN,OUT)\) (Wang et al. 2013) | This formalism proposed to model weighted FPRs and implement weighted reasoning based on the SNP system model |
\(DAFPN=(P;T;I;O;D;\alpha ;\beta ;W;U;Th;M)\) (Liu et al. 2013a) | This formalism proposed to overcome unreasonable points in the defection of FPN |
\(\textit{DAFPN}=(P;T;I;O;D;\alpha ;\beta ;W;U;Th_I ;Th_O ;M)\) Liu (2013b) | This formalism divided the threshold in two: input and output values, respectively |
Rights and permissions
About this article
Cite this article
Zhou, KQ., Zain, A.M. Fuzzy Petri nets and industrial applications: a review. Artif Intell Rev 45, 405–446 (2016). https://doi.org/10.1007/s10462-015-9451-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10462-015-9451-9