Skip to main content

Advertisement

Springer Nature Link
Log in

Covering-based intuitionistic fuzzy rough sets and applications in multi-attribute decision-making

  • Published:
Artificial Intelligence Review Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

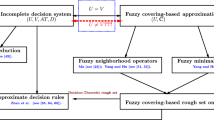
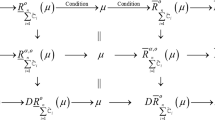
Covering based intuitionistic fuzzy (IF) rough set is a generalization of granular computing and covering based rough sets. By combining covering based rough sets, IF sets and fuzzy rough sets, we introduce three classes of coverings based IF rough set models via IF\(\beta \)-neighborhoods and IF complementary \(\beta \)-neighborhood (IFC\(\beta \)-neighborhood). The corresponding axiomatic systems are investigated, respectively. In particular, the rough and precision degrees of covering based IF rough set models are discussed. The relationships among these types of coverings based IF rough set models and covering based IF rough set models proposed by Huang et al. (Knowl Based Syst 107:155–178, 2016). Based on the theoretical analysis for coverings based IF rough set models, we put forward intuitionistic fuzzy TOPSIS (IF-TOPSIS) methodology to multi-attribute decision-making (MADM) problem with the evaluation of IF information problem. An effective example is to illustrate the proposed methodology. Finally, we deal with MADM problem with the evaluation of fuzzy information based on CFRS models. By comparative analysis, we find that it is more effective to deal with MADM problem with the evaluation of IF information based on CIFRS models than the one with the evaluation of fuzzy information based on CFRS models.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Alcantud JCR (2002) Revealed indifference and models of choice behavior. J Math Psychol 46:418–430

    Article  MathSciNet  MATH  Google Scholar 

  • Alcantud JCR, Torra V (2018) Decomposition theorems and extension principles for hesitant fuzzy sets. Inf Fusion 41:48–56

    Article  Google Scholar 

  • Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Set Syst 20:87–96

    Article  MATH  Google Scholar 

  • Atanassov KT, Pasi G, Yager RR (2015) Intuitionistic fuzzy interpretations of multi-criteria multi-person and multi-measurement tool decision-making. Int J Syst Sci 36:859–868

    Article  MathSciNet  MATH  Google Scholar 

  • Bonikowski Z, Bryniarski E, Wybraniec-Skardowska U (1998) Extensions and intentions in rough set theory. Inf Sci 107:149–167

    Article  MathSciNet  MATH  Google Scholar 

  • Chen CT (2000) Extensions of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Set Syst 114:1–9

    Article  MATH  Google Scholar 

  • Chen DG, Li W, Zhang X, Kwong S (2014) Evidence-theory-based numerical algorithms of attribute reduction with neighborhood-covering rough sets. Int J Approx Reason 55:908–923

    Article  MathSciNet  MATH  Google Scholar 

  • Chen DG, Zhang X, Li W (2015) On measurements of covering rough sets based on granules and evidence theory. Inf Sci 317:329–348

    Article  MathSciNet  MATH  Google Scholar 

  • Chen TY (2011) A comparative analysis of score functions for multiple criteria decision-making in intuitionistic fuzzy settings. Inf Sci 181:3652–3676

    Article  Google Scholar 

  • Cornelis C, Cock MD, Kerre EE (2003) Intuitionistic fuzzy rough sets: at the crossroads of imperfect knowledge. Expert Syst 20(5):260–270

    Article  Google Scholar 

  • Dai JH, Hu H, Wu WZ, Qian YH, Huang DB (2018) Maximal discernibility pairs based approach to attribute reduction in fuzzy rough sets. IEEE Trans Fuzzy Syst 26(4):2174–2187

    Article  Google Scholar 

  • Dai JH, Wei BJ, Zhang XH, Zhang QH (2017) Uncertainty measurement for incomplete interval-valued information systems based on \(\alpha \)-weak similarity. Knowl Based Syst 136:159–171

    Article  Google Scholar 

  • D’eer L, Cornelis C, Godo L (2017) Fuzzy neighborhood operators based on fuzzy coverings. Fuzzy Sets Syst 312:17–35

    Article  MathSciNet  MATH  Google Scholar 

  • D’eer L, Restrepro M, Cornelis C, Gomez J (2016) Neighborhood operators for coverings based rough sets. Inf Sci 336:21–44

    Article  MATH  Google Scholar 

  • Deng T, Chen Y, Xu W, Dai Q (2007) A novel approach to fuzzy rough sets based on a fuzzy covering. Inf Sci 177:2308–2326

    Article  MathSciNet  MATH  Google Scholar 

  • Dubois D, Prade H (1990) Rough fuzzy sets and fuzzy rough sets. Int J Gen Syst 17:191–209

    Article  MATH  Google Scholar 

  • Hu BQ (2015) Generalized interval-valued fuzzy variable precision rough sets determined by fuzzy logical operators. Int J Gen Syst 44:849–875

    Article  MathSciNet  MATH  Google Scholar 

  • Hu J, Pedrycz W, Wang G (2016) A roughness measure of fuzzy sets from the perspective of distance. Int J Gen Syst 45:352–367

    Article  MathSciNet  MATH  Google Scholar 

  • Huang B, Guo C, Zhang Y, Li H, Zhou X (2014) Intuitionistic fuzzy multigranulation rough sets. Inf Sci 277:299–320

    Article  MathSciNet  MATH  Google Scholar 

  • Huang B, Guo C, Zhang Y, Li H, Zhou X (2016) An intuitionistic fuzzy graded covering rough sets. Knowl Based Syst 107:155–178

    Article  Google Scholar 

  • Hwang CL, Yoon KS (1981) Multiple attibute decision methods and applications. Springer, Berlin

    Google Scholar 

  • Li LQ, Jin Q, Hu K, Zhao FF (2017) The axiomatic characterizations on L-fuzzy covering-based approximation operators. Int J Gen Syst 46:332–353

    Article  MathSciNet  Google Scholar 

  • Li TJ, Leung Y, Zhang WX (2008) Generalized fuzzy rough approximation operators based on fuzzy covering. Int J Approx Reason 48:836–856

    Article  MathSciNet  MATH  Google Scholar 

  • Liu GL, Sai Y (2009) A comparison of two types of rough sets induced by coverings. Int J Approx Reason 50:521–528

    Article  MathSciNet  MATH  Google Scholar 

  • Luce RD (1956) Semiorders and a theory of utility discrimination. Econometrica 24:178–191

    Article  MathSciNet  MATH  Google Scholar 

  • Ma L (2012) On some types of neighborhood-related covering rough sets. Int J Approx Reason 53:901–911

    Article  MathSciNet  MATH  Google Scholar 

  • Ma L (2015) Some twin approximation operators on covering approximation spaces. Int J Approx Reason 56:59–70

    Article  MathSciNet  MATH  Google Scholar 

  • Ma L (2016) Two fuzzy coverings rough set models and their generalizations over fuzzy lattices. Fuzzy Sets Syst 294:1–17

    Article  MathSciNet  MATH  Google Scholar 

  • Mardani A, Jusoh A, Zavadskas EK (2015) Fuzzy multiple criteria decision-making techniques and applications—two decades review from 1994 to 2014. Expert Syst Appl 42(8):4126–4148

    Article  Google Scholar 

  • Pawlak Z (1982) Rough sets. Int J Comput Inf Sci 11(5):341–356

    Article  MATH  Google Scholar 

  • Pomykala JA (1987) Approximation operations in approximation spaces. Bull Pol Acad Sci Math 35:653–662

    MathSciNet  MATH  Google Scholar 

  • She Y, He X (2014) Rough approximation operators on \(R_0\)-algebras (nilpotent minimum algebras) with an application in formal logic \(L^*\). Inf Sci 277:71–89

    Article  MATH  Google Scholar 

  • She Y, He X, Shi H, Qian Y (2017) A multiple-valued logic approach for multigranulation rough set model. Int J Approx Reason 82:270–284

    Article  MathSciNet  MATH  Google Scholar 

  • She Y, Li J, Yang H (2015) A local approach to rule induction in multi-scale decision tables. Knowl Based Syst 89:398–410

    Article  Google Scholar 

  • Sun BZ, Ma W (2011) Fuzzy rough set model on two different universes and its application. Appl Math Model 35(4):1798–1809

    Article  MathSciNet  MATH  Google Scholar 

  • Sun BZ, Ma W (2014) Soft fuzzy rough sets and its application in decision-making. Artif Intell Rev 41(1):67–80

    Article  Google Scholar 

  • Sun BZ, Ma W (2016) An approach to evaluation of emergency plans for unconventional emergency events based on soft fuzzy rough set. Kybernetes 45(3):1–26

    MathSciNet  Google Scholar 

  • Sun BZ, Ma W, Liu Q (2013) An approach to decision-making based on intuitionistic fuzzy rough sets over two universes. J Oper Res Soc 64:1079–1089

    Article  Google Scholar 

  • Sun BZ, Ma W, Xiao X (2017) Three-way group decision-making based on multigranulation fuzzy decision-theoretic rough set over two universes. Int J Approx Reason 81:87–102

    Article  MathSciNet  MATH  Google Scholar 

  • Sun BZ, Ma W, Zhao H (2013) A fuzzy rough set approach to emergrncy matrial demand prediction over two universe. Appl Math Model 37:7062–7070

    Article  MathSciNet  MATH  Google Scholar 

  • Szmidt E, Kacprzyk J (2000) Distances between intuitionistic fuzzy sets. Fuzzy Sets Syst 114:505–518

    Article  MathSciNet  MATH  Google Scholar 

  • Tsang ECC, Chen D, Yeung DS (2008) Approximations and reducts with covering generalized rough sets. Comput Appl Math 56:279–289

    Article  MathSciNet  MATH  Google Scholar 

  • Wang W, Xin X (2005) Distance between intuitionistic fuzzy sets. Pattern Recognit Lett 26:2063–2069

    Article  Google Scholar 

  • Xu WH, Zhang WX (2007) Measuring roughness of generalized rough sets induced a covering. Fuzzy Sets Syst 158:2443–2455

    Article  MathSciNet  MATH  Google Scholar 

  • Xu ZS (2007) Intuitionistic fuzzy aggregation operators. IEEE Trans Fuzzy Syst 15:1179–1187

    Article  Google Scholar 

  • Xu ZS (2010) A deviation-based approach to intuitionistic fuzzy multiple attribute group decision-making. Group Decis Negot 19:57–76

    Article  Google Scholar 

  • Xu ZS (2012) Intuitionistic fuzzy multiattribute decision-making: an interactive method. IEEE Trans Fuzzy Syst 20:514–525

    Article  Google Scholar 

  • Xu ZS, Yager RR (2006) Some geometric aggregation operators based on intuitionistic fuzzy sets. Int J Gen Syst 35:417–433

    Article  MathSciNet  MATH  Google Scholar 

  • Xu ZS, Yager RR (2008) Dynamic intuitionistic fuzzy multi-atribute decision-making. Int J Approx Reason 48:246–252

    Article  MATH  Google Scholar 

  • Xu ZS, Zhao N (2016) Information fusion for intuitionistic fuzzy decision-making: an overview. Inf Fusion 28:10–23

    Article  Google Scholar 

  • Yang B, Hu BQ (2016) A fuzzy covering-based rough set model and its generalization over fuzzy lattice. Inf Sci 367–368:463–486

    Article  Google Scholar 

  • Yang B, Hu BQ (2017) On some types of fuzzy covering-based on rough sets. Fuzzy Sets Syst 312:36–65

    Article  MathSciNet  MATH  Google Scholar 

  • Yao YY (1998) Relational interpretations of neighborhood operators and rough set approximation operators. Inf Sci 111:239–259

    Article  MathSciNet  MATH  Google Scholar 

  • Yao YY (2010) Three-way decisions with probabilistic rough sets. Inf Sci 180:341–353

    Article  MathSciNet  Google Scholar 

  • Yao YY (2016) Three-way decisions and cognitive computing. Congit Comput 8(4):543–554

    Google Scholar 

  • Yao YY, Yao B (2012) Covering based rough set approximations. Inf Sci 200:91–107

    Article  MathSciNet  MATH  Google Scholar 

  • Yue ZL (2014) TOPSIS-based group decision-making methodology in intuitionistic fuzzy setting. Inf Sci 277:141–153

    Article  MathSciNet  MATH  Google Scholar 

  • Żakowski W (1983) Approximations in the space \((U, \Pi )\). Demonstr Math XVI:761–769

    MATH  Google Scholar 

  • Zhan J, Alcantud JCR (2018) A novel type of soft rough covering and its application to multicriteria group decision-making. Artif Intell Rev. https://doi.org/10.1007/s10462-018-9617-3

    Article  Google Scholar 

  • Zhang XH, Miao D, Liu C, Le M (2016) Constructive methods of rough approximation operators and multigranulation rough sets. Knowl Based Syst 91:114–125

    Article  Google Scholar 

  • Zhang XY, Miao DQ (2017) Three-way attribute reducts. Int J Approx Reason 88:401–434

    Article  MathSciNet  MATH  Google Scholar 

  • Zhang ZM (2012) Generalized intuitionistic fuzzy rough sets based on intuitionistic fuzzy coverings. Inf Sci 198:186–206

    Article  MathSciNet  MATH  Google Scholar 

  • Zhang ZM (2013) Generalized Atanassov’s intuitionistic fuzzy power geometric operators and their application to multiple attribute group decision-making. Inf Fusion 14:460–486

    Article  Google Scholar 

  • Zhou L, Wu WZ (2008) On generalized intuitionistic fuzzy rough approximation operators. Inf Sci 178:2448–2465

    MathSciNet  MATH  Google Scholar 

  • Zhu P (2011) Covering rough sets based on neighborhoods: an approach without using neighborhoods. Int J Approx Reason 52:461–472

    Article  MathSciNet  MATH  Google Scholar 

  • Zhu W (2007) Topological approaches to covering rough sets. Inf Sci 177:1499–1508

    Article  MathSciNet  MATH  Google Scholar 

  • Zhu W (2009) Relationship between generalized rough sets based on binary relation and covering. Inf Sci 179(3):210–225

    Article  MathSciNet  MATH  Google Scholar 

  • Zhu W, Wang F (2007) On three types of covering rough sets. IEEE Trans Knowl Data Eng 19:1131–1144

    Article  Google Scholar 

Download references

Acknowledgements

The authors are extremely grateful to the editor and four anonymous referees for their valuable comments and helpful suggestions which helped to improve the presentation of this paper. The first author was supported by the NNSFC (11461025, 11561023). The second author was supported by the NNSFC (71571090), the National Science Foundation of Shaanxi Province of China (2017JM7022), the Key Strategic Project of Fundamental Research Funds for the Central Universities (JBZ170601).

Author information

Authors and Affiliations

  1. Department of Mathematics, Hubei University for Nationalities, Enshi, 445000, China

    Jianming Zhan

  2. School of Economics and Management, Xidian University, Xi’an, 710071, China

    Bingzhen Sun

Authors
  1. Jianming Zhan
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Bingzhen Sun
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Jianming Zhan.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhan, J., Sun, B. Covering-based intuitionistic fuzzy rough sets and applications in multi-attribute decision-making. Artif Intell Rev 53, 671–701 (2020). https://doi.org/10.1007/s10462-018-9674-7

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10462-018-9674-7

Keywords