Abstract
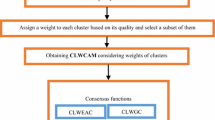
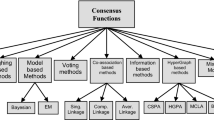
Clustering ensemble has been increasingly popular in the recent years by consolidating several base clustering methods into a probably better and more robust one. However, cluster dependability has been ignored in the majority of the presented clustering ensemble methods that exposes them to the risk of the low-quality base clustering methods (and consequently the low-quality base clusters). In spite of some attempts made to evaluate the clustering methods, it seems that they consider each base clustering individually regardless of the diversity. In this study, a new clustering ensemble approach has been proposed using a weighting strategy. The paper has presented a method for performing consensus clustering by exploiting the cluster uncertainty concept. Indeed, each cluster has a contribution weight computed based on its undependability. All of the predicted cluster tags available in the ensemble are used to evaluate a cluster undependability based on an information theoretic measure. The paper has proposed two measures based on cluster undependability or uncertainty to estimate the cluster dependability or certainty. The multiple clusters are reconciled through the cluster uncertainty. A clustering ensemble paradigm has been proposed through the proposed method. The paper has proposed two approaches to achieve this goal: a cluster-wise weighted evidence accumulation and a cluster-wise weighted graph partitioning. The former approach is based on hierarchical agglomerative clustering and co-association matrices, while the latter is based on bi-partite graph formulating and partitioning. In the first step of the former, the cluster-wise weighing co-association matrix is proposed for representing a clustering ensemble. The proposed approaches have been then evaluated on 19 real-life datasets. The experimental evaluation has revealed that the proposed methods have better performances than the competing methods; i.e. through the extensive experiments on the real-world datasets, it has been concluded that the proposed method outperforms the state-of-the-art. The substantial experiments on some benchmark data sets indicate that the proposed methods can effectively capture the implicit relationship among the objects with higher clustering accuracy, stability, and robustness compared to a large number of the state-of-the-art techniques, supported by statistical analysis.









Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Alizadeh H, Minaei-Bidgoli B, Parvin H (2014) To improve the quality of cluster ensembles by selecting a subset of base clusters. J Exp Theor Artif Intell 26(1):127–150
Alizadeh H, Yousefnezhad M, Minaei-Bidgoli B (2015) Wisdom of crowds cluster ensemble. Intell Data Anal 19(3):485–503
Alsaaideh B, Tateishi R, Phong DX, Hoan NT, Al-Hanbali A, Xiulian B (2017) New urban map of Eurasia using MODIS and multi-source geospatial data. Geo-Spat Information Science 20(1):29–38
Azimi J, Fern X (2009) Adaptive cluster ensemble selection. In: Proceedings of IJCAI, pp 992–997
Bache K, Lichman M (2013) UCI machine learning repository [Online]. http://archive.ics.uci.edu/ml
Chakraborty D, Singh S, Dutta D (2017) Segmentation and classification of high spatial resolution images based on Hölder exponents and variance. Geo-spatial Inf Sci 20(1):39–45
Charon I, Denoeud L, Guénoche A, Hudry O (2006) Maximum transfer distance between partitions. J Classif 23(1):103–121
Coretto P, Hennig Ch (2010) A simulation study to compare robust clustering methods based on mixtures. Adv Data Anal Classif 4:111–135
Cristofor D, Simovici D (2002) Finding median partitions using information-theoretical-based genetic algorithms. J Univers Comput Sci 8(2):153–172
Deng Q, Wu S, Wen J, Xu Y (2018) Multi-level image representation for large-scale image-based instance retrieval. CAAI Trans Intell Technol 3(1):33–39
Denoeud L (2008) Transfer distance between partitions. Adv Data Anal Classif 2:279–294
Dueck D (2009) Affinity propagation: clustering data by passing messages, Ph.D. dissertation, University of Toronto
Fern XZ, Brodley CE (2004) Solving cluster ensemble problems by bi-partite graph partitioning. In: Proceedings of international conference on machine learning (ICML)
Franek L, Jiang X (2014) Ensemble clustering by means of clustering embedding in vector spaces. Pattern Recogn 47(2):833–842
Fred ALN, Jain AK (2005) Combining multiple clusterings using evidence accumulation. IEEE Trans Pattern Anal Mach Intell 27(6):835–850
Frey BJ, Dueck D (2007) Clustering by passing messages between data points. Science 315:972–976
García-Escudero LA, Gordaliza A, Matrán C, Mayo-Iscar A (2010) A review of robust clustering methods. Adv Data Anal Classif 4:89–109
Guénoche A (2011) Consensus of partitions: a constructive approach. Adv Data Anal Classif 5:215–229
Hennig B (2008) Dissolution point and isolation robustness: robustness criteria for general cluster analysis methods. J Multivar Anal 99:1154–1176
Huang D, Lai JH, Wang CD (2015) Combining multiple clusterings via crowd agreement estimation and multi-granularity link analysis. Neurocomputing 170:240–250
Iam-On N, Boongoen T, Garrett S (2008) Refining pairwise similarity matrix for cluster ensemble problem with cluster relations. In: Proceedings of international conference on discovery science (ICDS), pp 222–233
Iam-On N, Boongoen T, Garrett S, Price C (2011) A link-based approach to the cluster ensemble problem. IEEE Trans Pattern Anal Mach Intell 33(12):2396–2409
Jain AK (2010) Data clustering: 50 years beyond k-means. Pattern Recogn Lett 31(8):651–666
Kettenring JR (2006) The practice of cluster analysis. J Classif 23:3–30
LeCun Y, Bottou L, Bengio Y, Haffner P (1998) Gradient-based learning applied to document recognition. Proc IEEE 86(11):2278–2324
Li T, Ding C (2008) Weighted consensus clustering. In: Proceedings of SIAM international conference on data mining (SDM)
Li Z, Wu XM, Chang SF (2012) Segmentation using superpixels: a bi-partite graph partitioning approach. In: Proceedings of IEEE conference on computer vision and pattern recognition (CVPR)
Li C, Zhang Y, Tu W et al (2017a) Soft measurement of wood defects based on LDA feature fusion and compressed sensor images. J For Res 28(6):1285–1292
Li X, Cui G, Dong Y (2017b) Graph regularized non-negative low-rank matrix factorization for image clustering. IEEE Trans Cybern 47(11):3840–3853
Li X, Cui G, Dong Y (2018a) Discriminative and orthogonal subspace constraints-based nonnegative matrix factorization. ACM TIST 9(6):65:1–65:24
Li X, Lu Q, Dong Y, Tao D (2018b) SCE: a manifold regularized set-covering method for data partitioning. IEEE Trans Neural Netw Learn Syst 29(5):1760–1773
Ma J, Jiang X, Gong M (2018) Two-phase clustering algorithm with density exploring distance measure. CAAI Trans Intell Technol 3(1):59–64
Mimaroglu S, Erdil E (2011) Combining multiple clusterings using similarity graph. Pattern Recogn 44(3):694–703
Mirzaei A, Rahmati M, Ahmadi M (2008) A new method for hierarchical clustering combination. Intell Data Anal 12(6):549–571
Ng AY, Jordan MI, Weiss Y (2002) On spectral clustering: Analysis and an algorithm. In: Advances in neural information processing systems (NIPS), pp 849–856
Nguyen TD, Welsch RE (2010) Outlier detection and robust covariance estimation using mathematical programming. Adv Data Anal Classif 4:301–334
Parvin H, Minaei-Bidgoli B (2015) A clustering ensemble framework based on selection of fuzzy weighted clusters in a locally adaptive clustering algorithm. Pattern Anal Appl 18(1):87–112
Peña JM, Lozano JA, Larrañaga P (1999) An empirical comparison of four initialization methods for the K-Means algorithm. Pattern Recogn Lett 20(10):1027–1040
Schynsa M, Haesbroeck G, Critchley F (2010) RelaxMCD: smooth optimisation for the minimum covariance determinant estimator. Comput Stat Data Anal 54:843–857
Song XP, Huang C, Townshend JR (2017) Improving global land cover characterization through data fusion. Geo-Spat Inf Sci 20(2):141–150
Spyrakis F, Benedetti P, Decherchi S, Rocchia W, Cavalli A, Alcaro S, Ortuso F, Baroni M, Cruciani G (2015) A pipeline to enhance ligand virtual screening: integrating molecular dynamics and fingerprints for ligand and proteins. J Chem Inform Model 55(10):2256–2274
Strehl A, Ghosh J (2003) Cluster ensembles: a knowledge reuse framework for combining multiple partitions. J Mach Learn Res 3:583–617
Topchy A, Jain AK, Punch W (2005) Clustering ensembles: models of consensus and weak partitions. IEEE Trans Pattern Anal Mach Intell 27(12):1866–1881
Wang T (2011) CA-Tree: a hierarchical structure for efficient and scalable coassociation-based cluster ensembles. IEEE Trans Syst Man Cybern B Cybern 41(3):686–698
Wang X, Yang C, Zhou J (2009) Clustering aggregation by probability accumulation. Pattern Recogn 42(5):668–675
Wang L, Leckie C, Kotagiri R, Bezdek J (2011) Approximate pairwise clustering for large data sets via sampling plus extension. Pattern Recogn 44(2):222–235
Wang CD, Lai JH, Zhu JY (2012) Graph-based multiprototype competitive learning and its applications. IEEE Trans Syst Man Cybern Part C Appl Rev 42(6):934–946
Wang B, Zhang J, Liu Y, Zou Y (2017) Density peaks clustering based integrate framework for multi-document summarization. CAAI Trans Intell Technol 2(1):26–30
Weiszfeld E, Plastria F (2009) On the point for which the sum of the distances to n given points is minimum. Ann Oper Res 167(1):7–41
Wolpert DH, Macready WG (1996) No free lunch theorems for search. Technical Report. SFI-TR-95-02-010. Citeseer
Wu J, Liu H, Xiong H, Cao J (2013) A theoretic framework of k-means based consensus clustering. In: proceedings of international joint conference on artificial intelligence
Xu L, Krzyzak A, Oja E (1993) Rival penalized competitive learning for clustering analysis, RBF net, and curve detection. IEEE Trans Neural Netw 4(4):636–649
Yu Z, Li L, Gao Y, You J, Liu J, Wong HS, Han G (2014) Hybrid clustering solution selection strategy. Pattern Recogn 47(10):3362–3375
Yu Z, Li L, Liu J, Zhang J, Han G (2015) Adaptive noise immune cluster ensemble using affinity propagation. IEEE Trans Knowl Data Eng 27(12):3176–3189
Zheng X, Zhu S, Gao J, Mamitsuka H (2015) Instance-wise weighted nonnegative matrix factorization for aggregating partitions with locally reliable clusters. In: Proceedings of IJCAI 2015, pp 4091–4097
Zhong C, Yue X, Zhang Z, Lei J (2015) A clustering ensemble: two-level-refined co-association matrix with path-based transformation. Pattern Recogn 48(8):2699–2709
Yang H, Yu L (2017) Feature extraction of wood-hole defects using wavelet-based ultrasonic testing. J For Res 28(2):395–402
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Rashidi, F., Nejatian, S., Parvin, H. et al. Diversity based cluster weighting in cluster ensemble: an information theory approach. Artif Intell Rev 52, 1341–1368 (2019). https://doi.org/10.1007/s10462-019-09701-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10462-019-09701-y