Abstract
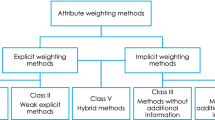
Attribute weighting is a key aspect when modeling multi-attribute decision analysis problems. Despite the large number of proposals reported in the literature, reaching a consensus on the most convenient method for a certain scenario is difficult, if not impossible. As a first contribution of this paper, we propose a categorization of existing methodologies, which goes beyond the current taxonomy (subjective, objective, hybrid). As a second contribution, supported by the new categorization, we survey and critically discuss the explicit weighting methods (which are closely related to the subjective ones). The critical discussion allows evaluating how much a solution can deviate from the expected one if no foresight is taken. As a final contribution, we summarize the main drawbacks from a global perspective and propose some insights to correct them. Such a discussion attempts to improve the reliability of decision support systems involving human experts.

Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Notes
The AIFS and non-AIVIFS values will be used for the sake of simplicity.
References
Allahi S, Mobin M, Vafadarnikjoo A, Salmon C (2015) An integrated AHP-GIS-MCLP method to locate bank branches. In: Proceedings of the (2015) industrial and systems engineering research conference Nashville. Tenn, USA
Aznar Bellver J, Martínez FG (2005) Nuevos métodos de valoración, 1-192. Editorial Universidad Politécnica de Valencia Madrid, Spain
Bana e Costa C, Vansnick JC, (1999) The MacBeth approach: basic ideas, software and an application. In: Meskens N, Roubens M (eds) Advances in decision analysis. Kluwer Academic Publishers, Dordrecht, Chicago, USA, pp 131–157
Bao T, Xie X, Long P, Wei Z (2017) MADM method based on prospect theory and evidential reasoning approach with unknown attribute weights under intuitionistic fuzzy environment. Expert Syst Appl 88:305–317
Bottomley PA, Doyle JR (2001) A comparison of three weight elicitation methods: good, better, and best. Omega 29:553–560
Chen T (2014) Interval-valued intuitionistic fuzzy QUALIFLEX method with a likelihood-based comparison approach for multiple criteria decision analysis. Inf Sci 261:149–169
Chen T, Li C (2010) Determining objective weights with intuitionistic fuzzy entropy measures: a comparative analysis. Inf Sci 180:4207–4222
Chen T, Li C (2011) Objective weights with intuitionistic fuzzy entropy measures and computational experiment analysis. Appl Soft Comput J 11(8):5411–5423
Chiclana F, Herrera F, Herrera-Viedma E (1998) Integrating three representation models in fuzzy multipurpose decision-making based on fuzzy preference relations. Fuzzy Sets Syst 97:33–48
Chin KS, Wang YM, Poon GK, Yang JB (2009) Failure mode and effects analysis using a group-based evidential reasoning approach. Comput Oper Res 36(6):1768–1779
Chin K, Fu C, Wang Y (2015) A method of determining attribute weights in evidential reasoning approach based on incompatibility among attributes. Comput Ind Eng 87:150–162
Churchman CW, Ackoff RL, Arnoff EL (1957) Introduction to operations research. Wiley, New York
Deng H, Yeh CH, Willis RJ (2000) Inter-company comparison using modified TOPSIS with objective weights. Comput Oper Res 27:963–973
Deng M, Yang J, Xu W (2004) Evidential reasoning and mathematical. Int J Inf Technol Decis Mak 3(3):419–428
Diakoulaki D, Mavrotas G, Papayannakis L (1995) Determining objective weights in multiple criteria problems: the critic method. Comput Oper Res 22:763–770
Doyle JR, Green RH, Bottomley PA (1997) Judging relative importance: direct rating and point allocation are not equivalent. Organ Behav Hum Decis Process 70(1):65–72
Edwards W (1977) How to use multiattribute utility measurement for social decision making. IEEE Trans Syst Man Cybernet 7(5):325–340
Edwards W, Hutton BF (1994) SMARTS and SMARTER: improved simple methods for multiattribute utility measurament. Organ Behav Hum Decis Process 60:306–325
Efendi YG (2010) Efektivitas Iklan Televisi Indosat IM3 “Online-Saykoji” Berdasarkan Direct Rating Method (DRM). Universitas Atma Jaya Yogyakarta, Tesis Sarjana dalam Ilmu Sosial. http://e-journal.uajy.ac.id/id/eprint/3226. Accessed Jan 2019
Fan Z, Ma J, Zhang Q (2002) An approach to multiple attribute decision making based on fuzzy preference information on alternatives. Fuzzy Sets Syst 131:101–106
Farhadinia B, Xu Z (2017) Distance and aggregation-based methodologies for hesitant fuzzy decision making, cognitive computation. Cognit Comput 9(1):81–94. https://doi.org/10.1007/s12559-016-9436-2
Farhadinia B, Xu Z (2018) Ordered weighted hesitant fuzzy information fusion-based approach to multiple attribute decision making with probabilistic linguistic term sets. Fundamenta Informaticae 159:361–383
Figueira J, Roy B (2002) Determining the weights of criteria in the ELECTRE type methods with a revised Simos. Eur J Oper Res 139:317–326
Fu C, Wang Y (2015) An interval difference based evidential reasoning approach with unknown attribute weights and utilities of assessment grades. Comput Ind Eng 81:109–117
Fu C, Yang SL (2010) The group consensus based evidential reasoning approach for multiple attributive group decision analysis. Eur J Oper Res 206(3):601–608
Fu C, Yang SL (2011) An attribute weight based feedback model for multiple attributive group decision analysis problems with group consensus requirements in evidential reasoning context. Eur J Oper Res 202(1):179–189
Fu C, Yang SL (2012) An evidential reasoning based consensus model for multiple attribute group decision analysis problems with interval-valued group consensus requirements. Eur J Oper Res 223:167–176
Fu C, Huhns M, Yang SL (2014) A consensus framework for multiple attribute group decision analysis in an evidential reasoning context. Inf Fusion 17:22–35
Guo S (2017) Application of entropy weight method in the evaluation of the road capacity of open area. In: AIP conference proceedings (the American Institute of Physics)
Herrera F, Herrera-Viedma E, Chiclana F (2001) Multiperson decision making based on multiplicative preference relations. Eur J Oper Res 129(2):372–385
Horowitz I, Zappe C (1995) The linear programming alternative to policy capturing for eliciting criteria weights in the performance appraisal process. Omega 23(6):667–676
Horsky D, Rao MR (1984) Estimation of attribute weights from preference comparisons. Manag Sci 30(7):801–822
Jahan A, Mustapha F, Sapuan SM, Yusof Ismail Md, Bahraminasab M (2012) A framework for weighting of criteria in ranking stage of material selection process. Int J Adv Manuf Technol 58:411–420
Jin F, Pei L, Chen H, Zhou L (2014) Interval-valued intuitionistic fuzzy continuous weighted entropy and its application to multi-criteria fuzzy group decision making. Knowl Based Syst 59:132–141
Keeney RL, Raiffa H (1976) Decisions with multiple objectives: preferences and value-tradeoffs. Wiley, New York
Khan MSA, Abdullah S, Ali A, Siddiqui N, Amin F (2017) Pythagorean hesitant fuzzy sets and their application to group decision making. J Intell Fuzzy Syst 33:3971–3985. https://doi.org/10.3233/JIFS-17811
Khan MSA, Ali A, Abdullah S, Amin F, Hussain F (2018) New extension of TOPSIS method based on pythagorean hesitant fuzzy sets with incomplete weight information. J Intell Fuzzy Syst 35:5435–5448. https://doi.org/10.3233/JIFS-171190
Kim SH, Ahn BS (1999) Interactive group decision making procedure under incomplete information. Eur J Oper Res 116:498–507
Lai YJ, Liu TY, Hwang CL (1994) TOPSIS for MODM. Eur J Oper Res 76(3):486–500
Lee JH, Han BJ, Lim HJ, Kim YD, Saxena N, Chung TM (2009) Optimizing access point allocation using genetic algorithmic approach for smart home environments. Comput J 52:938–949
Li DF (1999) Fuzzy multiattribute decision-making models and methods with incomplete preference information. Fuzzy Sets Syst 106:113–119
Li DF (2011) Closeness coefficient based nonlinear programming method for interval-valued intuitionistic fuzzy multiattribute decision making with incomplete preference information. Appl Soft Comput 11:3402–3418
Li M, Wu C (2016) A distance model of intuitionistic fuzzy cross entropy to solve preference problem on alternatives. Math Probl Eng 08:1–9
Liang GS (1999) Fuzzy MCDM based on ideal and antiPts. Eur J Oper Res 112:682–691
Liang W, Zhang X, Liu M (2015) The maximizing deviation method based on interval-valued pythagorean fuzzy weighted aggregating operator for multiple criteria group decision analysis. Discrete Dyn Nat Soc. https://doi.org/10.1155/2015/746572
Liu S, Chan FTS, Ran W (2016) Decision making for the selection of cloud vendor: an improved approach under group decision-making with integrated weights and objective/subjective attributes. Expert Syst Appl 55:37–47
Ma J, Fan ZP, Huang LH (1999a) A subjective and objective integrated approach to determine attribute weights. Eur J Oper Res 112:397–404
Ma J, Zhang Q, Zhou D, Fan ZP (1999b) A subjective and objective integrated approach to multiple attribute decision making with preference information on alternatives, pp 1–19
Park DG, Kwun YC, Park JH, Park IY (2009) Correlation coefficient of interval-valued intuitionistic fuzzy sets and its application to multiple attribute group decision making problems. Math Comput Model 50(9–10):1279–1293
Park JH, Park IY, Kgun YC, Tan X (2011) Extension of the TOPSIS method for decision making problems under interval-valued intuitionistic fuzzy environment. Appl Math Model 35:2544–2556
Pecchia L, Crispino F, Morgan SP (2014) A software tool to support the Health Technology Assessment (HTA) and the user need elicitation of medical devices via the analytic hierarchy process (AHP). In: Zhang YT (ed) The international conference on health informatics. IFMBE Proceedings, vol 42. Springer, Cham, pp 292–295
Pei Z (2013) Rational decision making models with incomplete weight information for production line assessment. Inf Sci 222:696–716
Qi X, Liang C, Zhang J (2015) Generalized cross-entropy based group decision making with unknown expert and attribute weights under interval-valued intuitionistic fuzzy environment. Comput Ind Eng 79:52–64
Ram M (2018) Advanced fuzzy logic approaches in engineering science (advances in mechatronics and mechanical engineering). IGI Global, Philadelphia
Rao RV, Patel BK, Parnichkun M (2011) Industrial robot selection using a novel decision making method considering objective and subjective preferences. Robot Auton Syst 59(6):367–375
Saaty TL (1977) A scaling method for priorities in hierarchical structures. J Math Psychol 15:234–281
Shirland LE, Jesse RR, Thompson RL, Iacovou CL (2003) Determining attribute weights using mathematical programming. Omega 31:423–437
Solymosi T, Dombi J (1986) A method for determining the weights of criteria: the centralized weights. Eur J Oper Res 26:35–41
Sun Q, Jiewen O (2015) Hesitant fuzzy multi-attribute decision making based on TOPSIS with entropy-weighted method. Manag Sci Eng 9(3):1–6
Valkenhoef G, Tervonen T (2016) Entropy-optimal weight constraint elicitation with additive multi-attribute utility models. Omega 64:1–12
Wan S, Dong J (2015) Interval-valued intuitionistic fuzzy mathematical programming method for hybrid multi-criteria group decision making with interval-valued intuitionistic fuzzy truth degrees. Inf Fusion 26:49–65
Wan SP, Li DF (2013) Fuzzy LINMAP approach to heterogeneous MADM considering comparisons of alternatives with hesitation degrees. Omega 41:925–940
Wan S, Li D (2014) Atanassov’s intuitionistic fuzzy programming method for heterogeneous multiattribute group decision making with Atanassov’s intuitionistic. IEEE Trans Fuzzy Syst 22(2):300–312
Wan S, Xu G, Wang F, Dong J (2015) A new method for Atanassov’s interval-valued intuitionistic fuzzy MAGDM with incomplete attribute weight information. Inf Sci 316(168):329–347
Wang Y (2005) On fuzzy multiattribute decision-making models and methods with incomplete preference information. Fuzzy Sets Syst 151:285–301
Wang YM, Fu GW (1993) Using multiobjective decision making method to make decision for multiattributes. Control Decis 8(1):25–29
Wang W, Liu X (2013) The multi-attribute decision making method based oninterval-valued intuitionistic fuzzy Einstein hybrid weighted geometric operator. Comput Math Appl 66:1845–1856
Wang Y, Luo Y (2010) Integration of correlations with standard deviations for determining attribute weights in multiple attribute decision making. Math Comput Model 51(1–2):1–12
Wang Y, Parkan C (2006) A general multiple attribute decision-making approach for integrating subjective preferences and objective information. Fuzzy Sets Syst 157:1333–1345
Wang YM, Yang JB, Xu DL (2006) Environmental impact assessment using the evidential reasoning approach. Eur J Oper Res 174(3):1885–1913
Xu Z, Zhang X (2013) Hesitant fuzzy multi-attribute decision making based on TOPSIS with incomplete weight information. Knowl Based Syst 52:53–64
Yager RR (2013) Pythagorean fuzzy subsets. In: Proceedings of joint IFSA world congress and NAFIPS annual meeting, Edmonton, Canada, pp 57–61
Yang JB (2001) Rule and utility based evidential reasoning approach for multiattribute decision analysis under uncertainties. Eur J Oper Res 131:31–61
Yang JB, Wang YM, Xu DL, Chin KS (2006) The evidential reasoning approach for MADA under both probabilistic and fuzzy uncertainties. Eur J Oper Res 171:309–343
Ye J (2013) Multiple attribute group decision-making methods with completely unknown weights in intuitionistic fuzzy setting and interval-valued intuitionistic fuzzy setting. Group Decis Negot 22:173–188
Zhang Y (2015) TOPSIS method based on entropy weight for supplier evaluation of power grid enterprise. In: 2nd international conference on education reform and modern management. https://download.atlantis-press.com/article/20912.pdf. Accessed Oct 2018
Zhang X (2016) Multicriteria Pythagorean fuzzy decision analysis: a hierarchical QUALIFLEX approach with the closeness index-based ranking methods. Inf Sci 330:104–124
Zhang X, Xu Z (2014) Extension of TOPSIS to multiple criteria decision making with pythagorean fuzzy sets. Int J Intell Syst 29(12):1061–1078
Zhang Q, Chen JCH, Chong PP (2004) Decision consolidation: criteria weight determination using multiple preference formats. Decis Support Syst 38:247–258
Zhang Y, Wang Y, Wang J (2014) Objective attributes weights determining based on Shannon information entropy in hesitant fuzzy multiple attribute decision making. Math Probl Eng. https://doi.org/10.1155/2014/463930
Zhou DN (2000) Fuzzy group decision support system approach to group decision making under multiple criteria. Ph.D. Dissertation, City University of Hong Kong, Hong Kong. https://scholars.cityu.edu.hk/en/theses/theses(7e93bfc7-acd8-4b8d-bc06-c8082316bac0).html. Accessed Oct 2018
Zhou L, Tao Z, Chen H, Liu J (2014) Continuous interval-valued intuitionistic fuzzy aggregation operators and their applications to group decision making. Appl Math Model 38:2190–2205
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Pena, J., Nápoles, G. & Salgueiro, Y. Explicit methods for attribute weighting in multi-attribute decision-making: a review study. Artif Intell Rev 53, 3127–3152 (2020). https://doi.org/10.1007/s10462-019-09757-w
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10462-019-09757-w