Skip to main content
Springer Nature Link
Log in

A quantum-based sine cosine algorithm for solving general systems of nonlinear equations

  • Published:
Artificial Intelligence Review Aims and scope Submit manuscript

Abstract

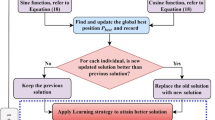
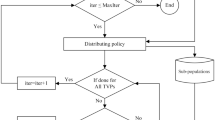
In this paper, a quantum-based sine cosine algorithm, named as Q-SCA, is proposed for solving general systems of nonlinear equations. The Q-SCA hybridizes the sine cosine algorithm (SCA) with quantum local search (QLS) for enhancing the diversity of solutions and preventing local optima entrapment. The essence of the proposed Q-SCA is to speed up the optimum searching operation and to accelerate the convergence characteristic. The proposed Q-SCA works in twofold: firstly, an improved version of SCA based on tuning the search space around the destination solution dynamically, so that the search space is shrunken gradually as the optima are attained. In addition, a new mechanism to update the solutions is introduced using bidirectional equations. Secondly, QLS is incorporated to improve the quality of the obtained solutions by the SCA phase. By this methodology, the proposed Q-SCA can achieve high levels of exploration/exploitation and precise stable convergence to high-quality solutions. The performance of the proposed algorithm is assessed by adopting twelve systems of nonlinear equations and two electrical applications. Furthermore, the proposed Q-SCA algorithm is applied on expensive large-scale problems including CEC 2017 benchmark and realistic optimal power dispatch (OPD) to confirm its scalability. Experimental results affirm that the Q-SCA is performs steadily, and it has a promising overall performance among several compared algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Abdollahi M, Isazadeh A, Abdollahi D (2013) Imperialist competitive algorithm for solving systems of nonlinear equations. Comput Math Appl 65(12):1894–1908

    MathSciNet  MATH  Google Scholar 

  • Abdollahi M, Abdollahi D, Bouyer A (2016) Improved cuckoo optimization algorithm for solving systems of nonlinear equations. J Supercomput 72(3):1246–1269

    Google Scholar 

  • Aydilek IB (2018) A hybrid firefly and particle swarm optimization algorithm for computationally expensive numerical problems. Applied Soft Comput 66:232–249

    Google Scholar 

  • Biswas PP, Suganthan PN, Mallipeddi R, Amaratunga GA (2018) Optimal power flow solutions using differential evolution algorithm integrated with effective constraint handling techniques. Eng Appl Artif Intell 68:81–100

    Google Scholar 

  • Bouchekara HREH (2014) Optimal power flow using black-hole-based optimization approach. Appl Soft Comput 24:879–888

    Google Scholar 

  • Dai J, Wu G, Wu Y, Zhu G (2008) Helicopter trim research based on hybrid genetic algorithm. In: World congress on intelligent control and automation, p 2007–2011. IEEE

  • Daryani N, Hagh MT, Teimourzadeh S (2016) Adaptive group search optimization algorithm for multi-objective optimal power flow problem. Appl Soft Comput 38:1012–1024

    Google Scholar 

  • Das S, Suganthan P (2011) Differential evolution: a survey of the state of-the-art. IEEE Trans Evol Comput 15(1):4–31

    Google Scholar 

  • Dorigo M, Maniezzo V, Colorni A (1996) The ant system: optimization by a colony of cooperating agents. IEEE Trans Syst Man Cybern B Cybern 26(1):29–41

    Google Scholar 

  • El-Sawy AA, Zaki EM, Rizk-Allah RM (2013) Novel hybrid ant colony optimization and firefly algorithm for multi-objective optimization problems. Int J Math Arch 4(1):152–161

    MATH  Google Scholar 

  • El-Sawy AA, Zaki EM, Rizk-Allah RM (2013) A novel hybrid ant colony optimization and firefly algorithm for solving constrained engineering design problems. J Nat Sci Math 6(1):1–22

    Google Scholar 

  • Floudas CA, Pardalos PM, Adjiman CS, Esposito WR, Gumus ZH, Harding ST, Klepeis JL, Meyer CA, Schweiger CA (1999) Handbook of test problems in local and global optimization. Kluwer Academic Publishers, Dordrecht

    MATH  Google Scholar 

  • Garcia S, Fernandez A, Luengo J, Herrera F (2009) A study of statistical techniques and performance measures for genetics-based machine learning, accuracy and interpretability. Soft Comput 13:959–977

    Google Scholar 

  • Goyel M (2007) Computer-based numerical & statistical techniques. Infinity Science Press LLC, Hingham

    Google Scholar 

  • Grosan C, Abraham A (2008) A new approach for solving nonlinear equations systems. IEEE Trans Syst Man Cybern part A 38(3):698–714

    Google Scholar 

  • Hashim FA, Houssein EH, Mabrouk MS, Al-Atabany W, Mirjalili S (2019) Henry gas solubility optimization: a novel physics-based algorithm. Future Generation Computer Systems 101:646–667

    Google Scholar 

  • Hoffman JD (2001) Numerical methods for engineers and scientists, 2nd edn. Marcel Dekker, New York

    MATH  Google Scholar 

  • Holland J (1975) Adaptation in natural and artificial systems. University of Michigan Press, Ann Arbor

    Google Scholar 

  • Jaberipour M, Khorram E, Karimi B (2011) Particle swarm algorithm for solving systems of nonlinear equations. Comput Math Appl 62(2):566–576

    MathSciNet  MATH  Google Scholar 

  • Jaeger G (2006) Quantum information: an overview. Springer, Berlin

    Google Scholar 

  • Jäger C, Ratz D (1995) A combined method for enclosing all solutions of nonlinear systems of polynomial equations. Reliab Comput 1(1):41–64

    MathSciNet  MATH  Google Scholar 

  • Kelley CT (2003) Solving nonlinear equations with Newton’s method, vol 1. SIAM, Philadelphia

    MATH  Google Scholar 

  • Kennedy J, Eberhart R (1995) Particle swarm optimization. Proc IEEE Int Conf Neural Netw 4:1942–1948

    Google Scholar 

  • Kumar AR, Premalatha L (2015) Optimal power flow for a deregulated power system using adaptive real coded biogeography-based optimization. Int J Electr Power Energy Syst 73:393–399

    Google Scholar 

  • Luo YZ, Tang GJ, Zhou LN (2008) Hybrid approach for solving systems of nonlinear equations using chaos optimization and quasi-Newton method. Appl Soft Comput 8(2):1068–1073

    Google Scholar 

  • Mo Y, Liu H, Wang Q (2009) Conjugate direction particle swarm optimization solving systems of nonlinear equations. Comput Math Appl 57(11):1877–1882

    MathSciNet  MATH  Google Scholar 

  • Mohamed AAA, Mohamed YS, El-Gaafary AAM, Hemeida AM (2017) Optimal power flow using moth swarm algorithm. Elec Power Syst Res 142:190–206

    Google Scholar 

  • Oliveira HA, Petraglia A (2013) Solving nonlinear systems of functional equations with fuzzy adaptive simulated annealing. Appl Soft Comput 13(11):4349–4357

    Google Scholar 

  • Ouyang A, Zhou Y, Luo Q (2009) Hybrid particle swarm optimization algorithm for solving systems of nonlinear equations. In: International conference on granular computing, GRC’09, p 460–465. IEEE

  • Pan WT (2012) A new fruit fly optimization algorithm: taking the financial distress model as an example. Knowl-Based Syst 26(2):69–74

    Google Scholar 

  • Pulluri H, Naresh R, Sharma V (2018) A solution network based on stud krill herd algorithm for optimal power flow problems. Soft Comput 22(1):159–176

    Google Scholar 

  • Rizk-Allah MR, Hassanien AE (2018c) New binary bat algorithm for solving 0–1 knapsack problem. Complex Intell Syst 4(1):31–53

    Google Scholar 

  • Rizk-Allah MR (2018d) An improved sine cosine algorithm based on orthogonal parallel information for global optimization. Soft Comput. https://doi.org/10.1007/s00500-018-3355-y

    Article  Google Scholar 

  • Rizk-Allah RM (2014) A novel multi-ant colony optimization for multi-objective resource allocation problems. Int J Math Arch 5(9):183–192

    Google Scholar 

  • Rizk-Allah RM (2016a) An improved firefly algorithm based on local search method for solving global optimization problems. Int J Manag Fuzzy Syst 2(6):51–57

    Google Scholar 

  • Rizk-Allah RM (2016b) Hybridization of fruit fly optimization algorithm and firefly algorithm for solving nonlinear programming problems. Int J Swarm Intel Evol Comput 5(2):1–10

    Google Scholar 

  • Rizk-Allah RM (2018) Hybridizing sine cosine algorithm with multi-orthogonal search strategy for engineering design problems. J Comput Des Eng 5(2):249–273

    MathSciNet  Google Scholar 

  • Rizk-Allah RM, Zaki EM, El-Sawy AA (2013) Hybridizing ant colony optimization with firefly algorithm for unconstrained optimization problems. Appl Math Comput 224(1):473–483

    MathSciNet  MATH  Google Scholar 

  • Rizk-Allah RM, El-Sehiemy RA, Deb S, Wang GG (2017) A novel fruit fly framework for multi-objective shape design of tubular linear synchronous motor. J Supercomput 73(3):1235–1256

    Google Scholar 

  • Rizk-Allah RM, Hassanien AE, Bhattacharyya S (2018) Chaotic crow search algorithm for fractional optimization problems. Appl Soft Comput 71:1161–1175

    Google Scholar 

  • Rizk-Allah RM, El-Sehiemy RA, Wang GG (2018) A novel parallel hurricane optimization algorithm for secure emission/economic load dispatch solution. Appl Soft Comput 63:206–222

    Google Scholar 

  • Rizk-Allah RM, Hassanien AE, Elhoseny M, Gunasekaran M (2019) A new binary salp swarm algorithm: development and application for optimization tasks. Neural Comput Appl 31(5):1641–1663

    Google Scholar 

  • Saadat H (1999) Power system analysis. McGraw-Hill, United States

    Google Scholar 

  • Seyedali Mirjalili SCA (2016) A sine cosine algorithm for solving optimization problems. Knowl-Based Syst 96:120–133

    Google Scholar 

  • Sharma JR, Arora H (2013) On efficient weighted-Newton methods for solving systems of nonlinear equations. Appl Math Comput 222:497–506

    MathSciNet  MATH  Google Scholar 

  • Sun J, Xu W, Feng B (2005) Adaptive parameter control for quantum-behavedparticle swarm optimization on individual level. Int Conf Syst, Man Cyber 4:3049–3054

    Google Scholar 

  • Turgut OE, Turgut MS, Coban MT (2014) Chaotic quantum behaved particle swarm optimization algorithm for solving nonlinear system of equations. Comput Math Appl 68(4):508–530

    MathSciNet  MATH  Google Scholar 

  • Wang C, Luo R, Wu K, Han B (2011) A new filled function method for an unconstrained nonlinear equation. J Comput Appl Math 235(6):1689–1699

    MathSciNet  MATH  Google Scholar 

  • Wang G-G, Gandomi AH, Yang X-S, Alavi AH (2014) A novel improved accelerated particle swarm optimization algorithm for global numerical optimization. Eng Comput 31(7):1198–1220. https://doi.org/10.1108/EC-10-2012-0232

    Article  Google Scholar 

  • Warid W (2020) Optimal power flow using the AMTPG-Jaya algorithm. Appl Soft Comput 91:106252

    Google Scholar 

  • Wolpert DH, Macready WG (1997) No free lunch theorems for optimization. IEEE Trans Evol Comput 1(1):67–82

    Google Scholar 

  • Wu Z, Kang L (2003) A fast and elitist parallel evolutionary algorithm for solving systems of non-linear equations. Proc Congr Evolut Comput 2:1026–1028

    Google Scholar 

  • Wu J, Cui Z, Liu J (2011) Using hybrid social emotional optimization algorithm with metropolis rule to solve nonlinear equations. In: IEEE 10th International conference on cognitive informatics and cognitive computing (ICCI-CC'11), p 405-411. IEEE

  • Xi M, Sun J, Xu W (2008) An improved quantum-behaved particle swarm optimization algorithm with weighted mean best position. Appl Math Comput 205(2):751–759

    MATH  Google Scholar 

  • Yang XS (2010) Engineering optimisation: an introduction with metaheuristic applications. Wiley, New York

    Google Scholar 

  • Yuan G, Lu X (2008) A new backtracking inexact BFGS method for symmetric nonlinear equations. Comput Math Appl 55(1):116–129

    MathSciNet  MATH  Google Scholar 

  • Zouache D, Nouioua F, Moussaoui A (2016) Quantum-inspired firefly algorithm with particle swarm optimization for discrete optimization problems. Soft Comput 20(7):2781–2799

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Engineering, Menoufia University, Shebin El-Kom, Egypt

    Rizk M. Rizk-Allah

Authors
  1. Rizk M. Rizk-Allah
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Rizk M. Rizk-Allah.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rizk-Allah, R.M. A quantum-based sine cosine algorithm for solving general systems of nonlinear equations. Artif Intell Rev 54, 3939–3990 (2021). https://doi.org/10.1007/s10462-020-09944-0

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10462-020-09944-0

Keywords